HTML
-
Quantitative phase imaging (QPI) is an effective optical technique used to visualize and measure variations in the optical thickness of unlabeled biological samples without the need for specific exogenous contrast agents1-3. Over the last few decades, significant progress has been made in the development of QPI technologies4-6, which have shown significant success in biomedical applications. The transport of intensity equation (TIE) is a well-established noninterferometric phase retrieval approach that enables QPI by measuring the intensities at multiple axially displaced planes7-9. TIE was derived under the assumption of monochromatic coherent illumination and paraxial approximation10, making it suitable for imaging systems with coherent sources and low-numerical-aperture (NA) objective, obtaining high-precision QPI11. In the case of an object illuminated by a partially coherent source, TIE is expected to realize improved spatial resolution beyond the coherence diffraction limit because the angular spread of the illumination contributes to lateral resolution enhancement12-14. However, the transfer response amplitude of the high-frequency information in the TIE-retrieved phase is significantly lost because of the coherence effect15. Furthermore, TIE is limited to brightfield microscopy and is not compatible with darkfield microscopy, hindering its application in large field of view (FOV) and high-resolution imaging. To address these challenges, we previously proposed a hybrid brightfield and darkfield transport of intensity (HBDTI) approach16 to realize high-throughput QPI.
HBDTI merges the forward image formation model with darkfield illumination based on the transport of intensity and employs an iterative solution to bypass the analytically modeled complex inverse problem. Therefore, HBDTI obtains a spatial imaging resolution 2.5 times beyond the incoherent diffraction limit in a large FOV, thereby solving the challenges for TIE in balancing high-throughput imaging. However, the optical non-uniformity of biological specimens and mechanical disturbances in the microscope body lead to time-varying aberrations and focus drift, significantly compromising the imaging performance for long-term research17. Additionally, aberration fluctuations are closely related to the sample and environment and cannot be compensated by fixed optical designs. As the coupling relationship between the object phase and pupil aberrations under partially coherent illumination is not explicitly considered in the derivation, HBDTI has difficulty in realizing high-throughput imaging with aberration correction. Therefore, achieving high-precision and high-resolution partially coherent illumination QPI over a wide FOV remains a key challenge.
Recently, a technique termed as computational adaptive optics (AO) has been developed to achieve aberration correction from an algorithmic perspective without introducing AO hardware. Based on this concept, the Fourier ptychographic microscopy (FPM)18, 19 enables direct aberration recovery and correction with the aid of inherent data redundancy, achieving high-quality QPI results20, 21. Additionally, these methods can further reduce data redundancy by introducing Zernike polynomial fitting strategies22-24. Hence, inspired by computational AO techniques, we propose a transport-of-intensity quantitative phase microscopy with aberration correction (TI-AC) approach that combines iterative phase retrieval, aberration correction, and pixel super-resolution to achieve high-throughput aberration-free QPI. TI-AC can remove the negative impact of spatially nonuniform and temporally varied aberrations through aberration correction, thereby enhancing the imaging quality for long-term studies. Compared to traditional TIE-based QPI methods (which need to satisfy the Nyquist-Shannon sampling criterion), the TI-AC method is compatible with sensors that have large pixel sizes to provide a four times wider FOV, enabling high-precision QPI even with 2× pixel binning.
-
Computational imaging methods comprise two main components: optical modulation and information processing25, 26. Optical modulation typically involves the spatial-temporal coherence illumination modulation (e.g., asymmetric illumination and multiwavelength scanning)27, aperture modulation28, and sensor defocus29. Usually, phase retrieval algorithms based on the transport of intensity generate phase contrast by introducing defocus on the pupil function to convert the phase information into intensity under brightfield illumination30, 31. Alternatively, annular NA-matched illumination can yield high-contrast defocused intensity images and enable an incoherent diffraction-limited spatial resolution14. Thus, the TI-AC method utilizes a through-focus intensity stack captured under an annular NA-matched illumination for robust measurements.
For information processing, TIE-based QPI methods generally establish a forward image formation model to derive the linear relationship between the object phase and measured intensity by introducing certain approximation conditions9. These methods can directly solve the inverse problem via deconvolution. These types of deconvolution methods that consider partially coherent illumination can provide high-resolution results. However, they cannot decouple the phase and aberrations in such linear models. Additionally, direct deconvolution methods (such as AI-TIE14 and DPC6) should satisfy the Nyquist-Shannon sampling criterion and are not compatible with sensors in pixel binning case (i.e., large pixel sizes). To address these issues, an iterative process is typically employed for phase retrieval to solve nonlinear models and achieve high-precision QPI13, 16. Therefore, our proposed TI-AC method is essentially an iterative phase recovery technique that combines pixel super-resolution and aberration correction to remove image degradation caused by an insufficient sampling rate and aberrations. It uses annular illumination to capture intensity images and realizes a resolution beyond the coherent diffraction limit, facilitating the decoupling of the sample phase and pupil function to improve the accuracy and efficiency of aberration correction.
The sensor pixel binning process is usually modeled as a spatial averaging operator $ {LRPixel}\,\, = \,\,\sum{a_h}/K^2 $, (h = 0, 1, $ \ldots $, $ K^2 $-1), where $ a_h $ denotes the gray value of the pixel super-resolution intensity images and K denotes a down-sampling factor ($ K = 3 $ in our study). By incorporating the sensor pixel binning model, the TI-AC method embeds a pixel super-resolution algorithm into the phase recovery and aberration correction process. During the upsampling process, we presume a reduction in the sensor’s actual pixel size by a factor of three to fulfill the Nyquist sampling criterion, with low-resolution images captured through the activation of pixel binning, where nine pixels are merged into a single pixel equivalent. Throughout the iterative update process, a computational supplementation of pixel binning was employed to accurately emulate the pixel aliasing issues encountered on the experimental platform.
The principle of the proposed TI-AC method is illustrated in Fig. 1 and the steps are as follows. Step 1: Collect N $ z $-axis measurements under annular NA-matched illumination as input data $ I_{mea}^n $, where $ n = 1, 2, \ldots$$ , N $ $ (N = 12) $. Step 2: Upsample the in-focus intensity image $ I_{up} $ and initialize the complex amplitude of the high-resolution sample $ O $. The pupil function $ \hat P $ is initialized to a circular distribution without phase aberration. Step 3: Based on the assumed high-resolution complex amplitude and annular NA-matched illumination distribution (represented by 12 point sources), obtain the intensity stack $ I_{i}^{n} $ at various illumination angles with different defocus distances by numerical propagation, where $ i $ denotes the diversity angle of the illumination [$ i = 1, 2, \ldots$$ , I $ $ (I = 12) $]. Step 4: Calculate the partially coherent illumination intensity $ I_{cal}^n $ based on $ I_{i}^{n} $ and then the measured intensity images $ I_{mea}^n $ can be decomposed into intensity components $ I_{dec, i}^n $ of the complex amplitude $ U_{i}^{n} $
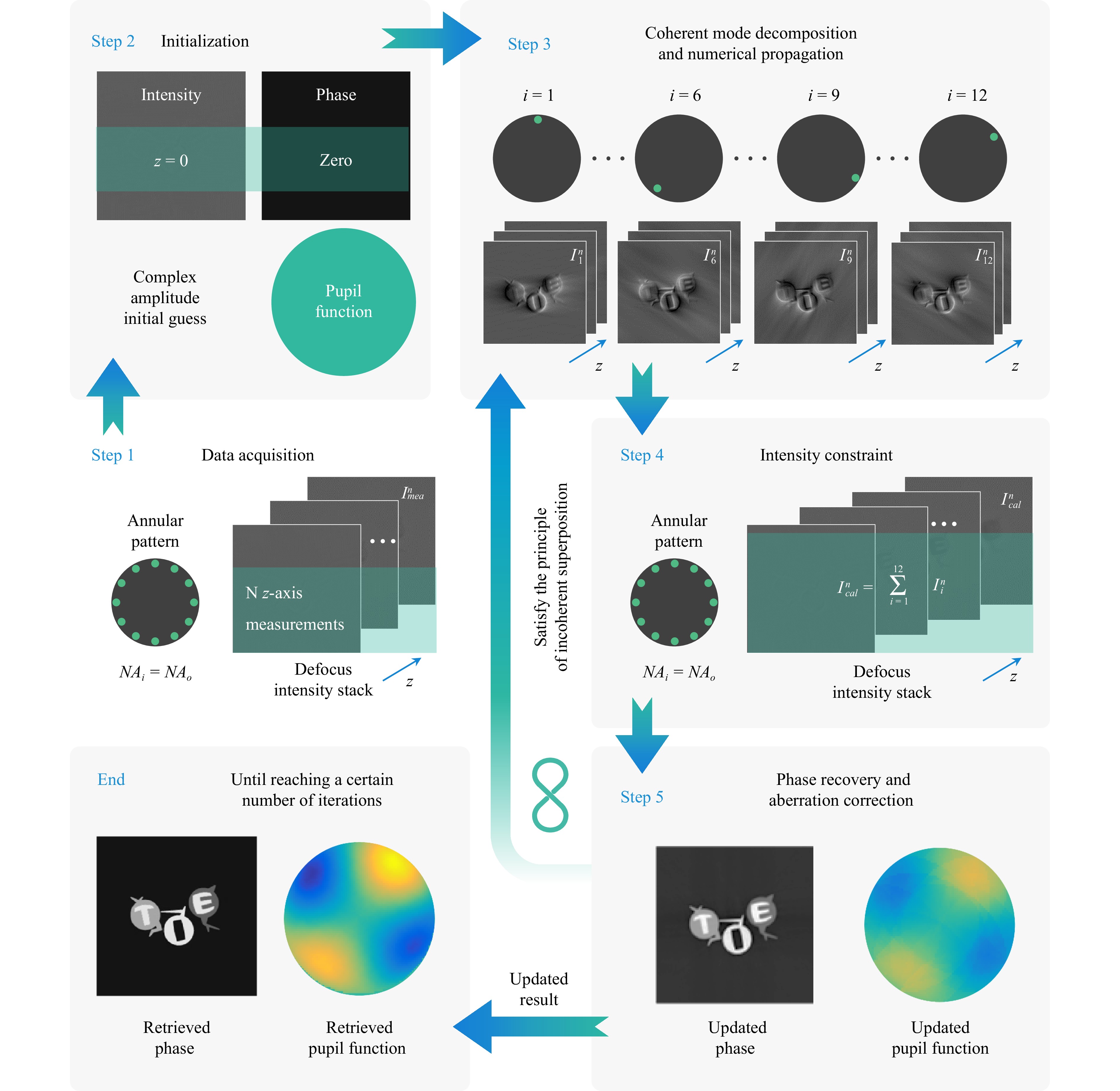
Fig. 1 Schematic diagram of TI-AC method. $I_{mea}^n$: measured intensity images, $I_{i}^{n}$: calculated intensity images at varying illumination angles with different defocus distances, $I_{cal}^n$: calculated partially coherent intensity images.
$$ I_{dec, i}^n({\bf{r}}) = \frac{|U_{i}^{n}({\bf{r}})|^2}{\sum_{i = 1}^{I = 12}I_{i}^{n}({\bf{r}})} I_{mea}^n({\bf{r}}) $$ (1) where $ {\bf{r}} $ denotes a two-dimensional coordinate system in real space. A decomposed intensity stack is used as a constraint to update the normalized complex amplitude. Step 5: The updated complex amplitude stacks on different planes are back-propagated to the in-focus plane. These propagated complex amplitude stacks are synthesized in the Fourier domain to update the complex amplitude of the object globally using difference map16, 32. Embedded aperture function recovery (EPRY) algorithm20 and Zernike polynomial constraint are used to correct the phase aberration. After updating the pupil function with EPRY to provide a physical prior constraint for the aberration, the n-order Zernike aberration polynomial constraint is used as the basis function for fitting the retrieved aberration to improve the convergence efficiency. The updated pupil function for the coherent ePIE scenario is revised to reflect the fact that TI-AC exclusively utilizes brightfield intensity images as input, as illustrated in Eq. 223, 33
$$ \hat{P}_i\left( {\bf{u}} \right) = \hat{P}\left( {\bf{u}} \right) +\alpha \frac{\hat{O}\left( {\bf{u}} \right) ^*}{|\hat{O}\left( {\bf{u}} \right) |^2}[{\hat{U}_i}^{(j)}\left( {\bf{u}} \right) -{\hat{U}_i}^{(j-1)}\left( {\bf{u}} \right) ] $$ (2) Global updating is then implemented using difference map32. Here, $ \hat{U}_i^{(j)}\left( {\bf{u}} \right) $ and $ \hat{U}_i^{(j-1)}\left( {\bf{u}} \right) $ are the Fourier spectrum with and without the intensity constraint respectively, $ j $ denotes the current iteration, $ {\bf{u}} $ denotes the spatial frequency coordinate corresponding to $ {\bf{r}} $, and $ \alpha $ denotes the updating step size. By repeating steps 3-5 until convergence, it is possible to retrieve the high-resolution complex amplitude with aberration correction.
To address the pixel binning and phase aberration issues in TIE, a TI-AC algorithm for phase retrieval is proposed. This algorithm incorporates aberration correction and pixel super-resolution. In this study, we implemented an adaptation of the EPRY algorithm, which diverges from its conventional form. Conventionally, the EPRY algorithm is contingent on darkfield in-focus intensity measurements. Conversely, our TI-AC approach exclusively leverages brightfield through-focus intensity stacks. This methodological departure necessitated refinement of the update formula within the aberration correction algorithm to accommodate the unique data inputs of our approach. Additionally, from the perspective of algorithm implementation, the TI-AC method employs a global updating strategy predicted on difference map32. Thus, the TI-AC method enables joint global optimization, avoiding the pitfalls of the traditional EPRY’s local optimization, where a single misstep can lead to complete failure. Furthermore, it ensures the realization of a stable and globally unique solution with improved convergence efficiency. Further details of the entire algorithm can be found in the Supporting Information.
-
For imaging systems that exhibit nonnegligible aberrations, the object spectrum and imaging aberrations are inseparable in the captured images. The use of annular NA-matched illumination aids in efficiently decoupling the sample phase and aberration23, 34, which has been validated in Fig. 2a. Fig. 2a shows the comparatively retrieved results obtained using 12 defocused intensity images under different illumination patterns. For the circular partially coherent illumination of Patterns 1 and 2, the number of images is insufficient to decouple the sample and aperture, resulting in inaccurate phase retrieval. Conversely, the annular NA-matched illumination corresponding to Pattern 3 exhibited favorable decoupling characteristics, enabling accurate aberration recovery with a smaller amount of data. Thus, the TI-AC method uses annular NA-matched illumination to capture intensities.
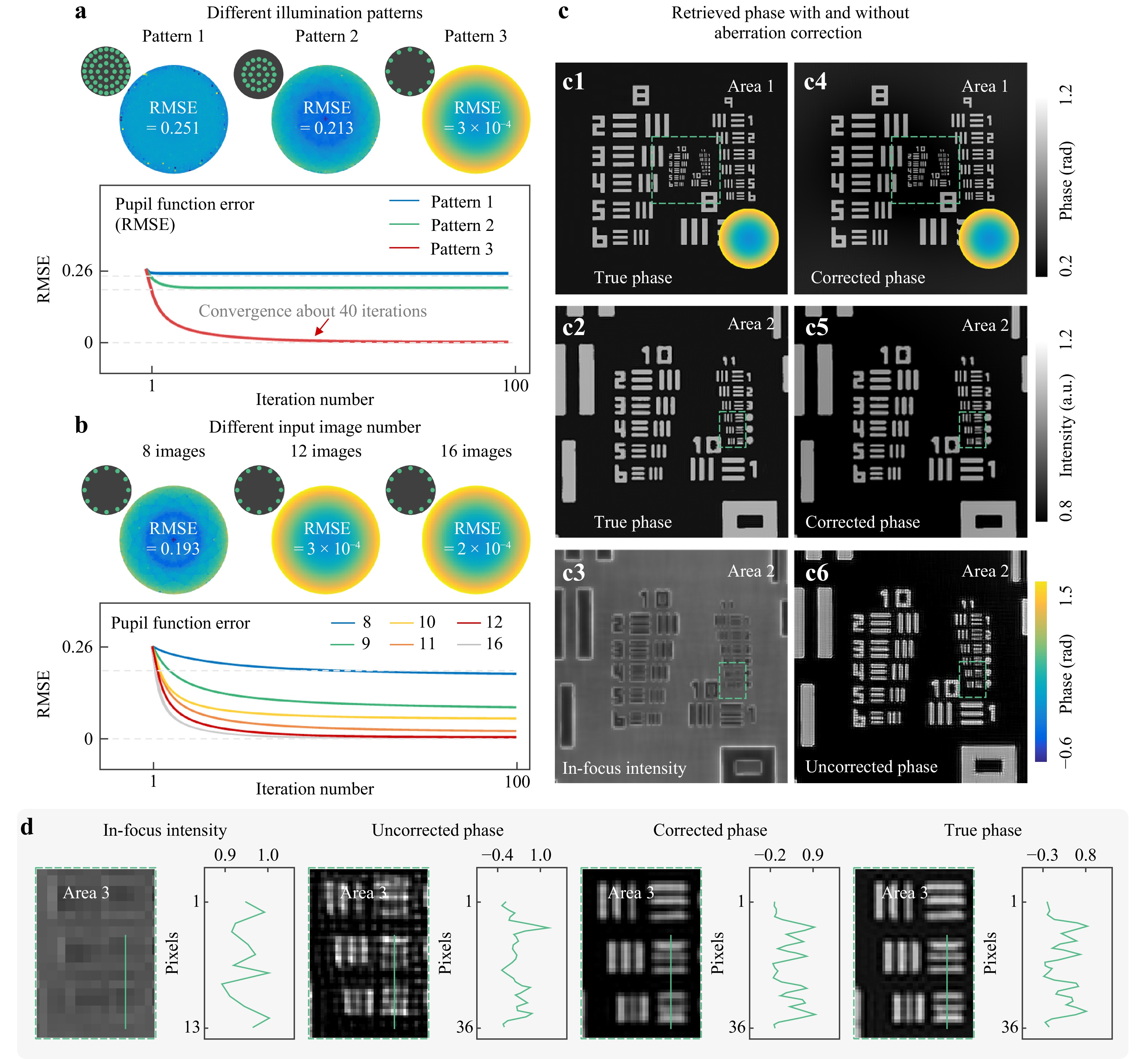
Fig. 2 Simulations of the proposed TI-AC method. a Comparison of aberration in different illumination modes under 12 images. b Comparison of aberration in different amount of data under the same illumination. c The true phase, corrected phase, intensity, and uncorrected phase. d The enlarged view of intensity, true phase, corrected phase, uncorrected phase, and profiles corresponding to the green lines.
-
In the ill-posed inverse phase retrieval problem, sufficient data redundancy is crucial for successful recovery35, 36. This requirement becomes more demanding when the additional retrieval of the system pupil is considered. Therefore, we verify the minimum data redundancy of the TI-AC method through simulations, as shown in Fig. 2b. Our findings indicate that by incorporating the uniform transmission assumption and Zernike polynomial constraint into the aberration recovery process, the TI-AC method can realize successful phase retrieval using 12 images under 12-piece light-emitting diode (LED) illumination. Furthermore, increasing the number of raw images does not significantly improve the quality of the retrieved phase. Thus, to enhance the imaging quality and reduce the data acquisition time, our TI-AC method employs an annular NA-matched illumination scheme with 12 intensity measurements. It should be noted that the Zernike polynomial constraint improves convergence efficiency. However, removing this constraint does not affect the phase retrieval accuracy of TI-AC.
-
To validate the feasibility of the proposed TI-AC method, simulation results of the resolution target are presented in Fig. 2c, d. The simulation parameters are as follows: 6.5 μm pixel size detector, 0.4 NA objective lens with a magnification of 10×, and 525 nm wavelength LED illumination. The simulated illumination is an annular LED array, which is the outermost 12-piece LED illumination. Its illumination NA matches that of the objective lens NA. The image formation under partially coherent illumination is simulated using Abbe’s method, and the phase aberration is shown at the bottom of Fig. 2c1. The original low-resolution image exhibits a resolution of 201 × 201 pixels. With less than 40 iterations, the TI-AC method can reconstruct the high-resolution phase and corresponding aberration at a resolution of 603 × 603 pixels. The insufficient sampling rate in the simulated low-resolution intensity image made it impossible to distinguish higher-frequency information [see Fig. 2d]. By contrast, TI-AC-retrieved phase exhibits more features with high contrast than the uncorrected phase, demonstrating its effectiveness in realizing high-resolution phase.
-
The capability of the proposed TI-AC method for pixel-super-resolution imaging can be validated using a quantitative phase target (Benchmark QPT). In this experiment, an inverted optical microscopy imaging system (IX83, Olympus) equipped with an electric defocus drive is used, as shown in Fig. 3a1, a2. The TI-AC method captures the intensity images under an annular NA-matched illumination configuration34, 37. To enable suitable annular illumination, a 12-piece LED illumination with a wavelength of 525 nm is employed as the light source. The 0.4 NA objective lens (Olympus, Tokyo, Japan) with a magnification of 10× is used to provide a large imaging FOV. To verify the pixel super-resolution imaging capability of our method, an sCMOS sensor (Hamamatsu, 2048 × 2048) with a pixel size of 6.5 μm is used to acquire the intensity image for which the Nyquist-Shannon sampling criterion is insufficient.
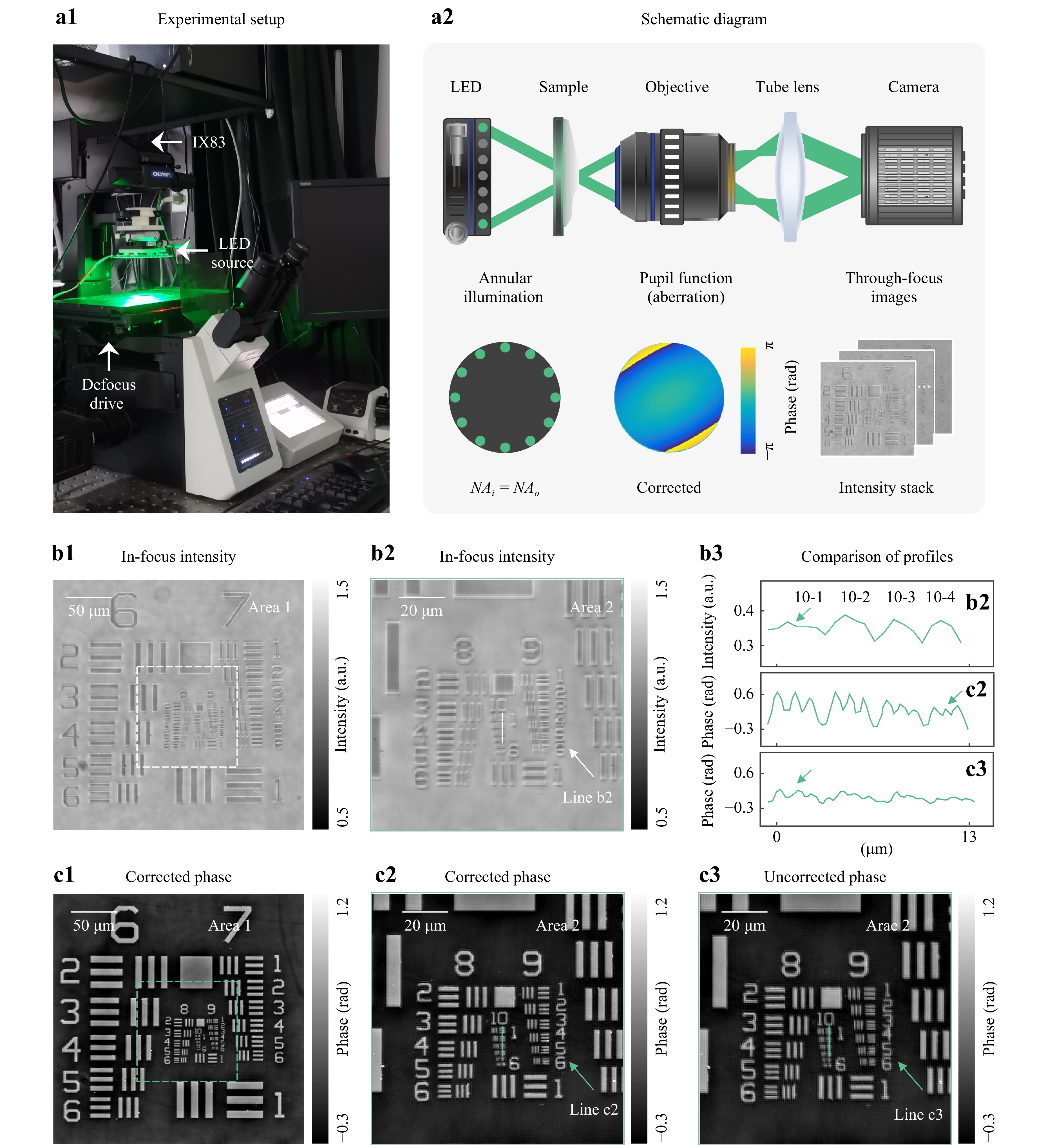
Fig. 3 Experimental results of QPT. a1 Experimental setup. a2 The schematic diagram of the optical system and retrieved aberration. b1 In-focus intensity. b2 The enlarged view of b1. b3 The corresponding profiles of intensity, corrected phase, and uncorrected phase. c1 TI-AC-retrieved phase with correction. c2, c3 The enlarged view of corrected and uncorrected phase.
In fact, it is challenging to acquire an in-focus intensity image within a wide FOV because the presence of unidentified minor defocused aberrations leads to captured intensity images exhibiting a specific level of imaging contrast, as depicted in Fig. 3b1. The proposed TI-AC method introduces defocus to convert phase information into intensity, and these through-focus intensity images provide ample phase contrast for accurate phase retrieval. However, owing to the limited sampling rate of the sensor, the intensity image suffered from a mosaic effect (Fig. 3b2), making it challenging to discern fine details such as element 6 in group 9. The TI-AC method realized convergence in 40 iterations (Fig. 3c1), and the reconstructed phase aberration can be observed in Fig. 3a2.
TI-AC explicitly considers the sensor pixel binning model, thereby directly embedding the pixel-super-resolution algorithm into the phase recovery and aberration correction process, thus simultaneously achieving pixel-super-resolution, aberration correction, and phase recovery. Compared to the retrieved phase without aberration correction (Fig. 3c3), the TI-AC-retrieved phase (Fig. 3c2) realizes a 2-fold resolution gain, reaching approximately ~345 nm half-pitch resolution and resolving the linewidth of group 10, element 4. This improvement is observed by comparing the profiles shown in Fig. 3b3, where the TI-AC method effectively removes the mosaic effect due to insufficient Nyquist-Shannon sampling criterion and achieves a maximum resolution consistent with the theoretical half-pitch resolution. This demonstrates that our method can effectively correct aberrations caused by the mechanical instability of the microscope to enhance the resolution of the imaging platform and achieve high-throughput transport-of-intensity QPI.
-
To evaluate the adaptive QPI ability of the TI-AC method, the imaging results for unlabeled live Henrietta Lacks (HeLa) cells are presented in Fig. 4. The phase retrieved using the proposed TI-AC method exhibits significantly improved resolution in distinguishing subcellular structures when compared to the uncorrected results. Considering spatially varying aberrations present in a large FOV, our proposed TI-AC method digitally divides the entire FOV into subregions to individually reconstruct the corresponding aberrations, thereby mitigating the impact of spatially varying aberrations. For example, the insets of Fig. 4a2, a3, b, c display the retrieved phase aberrations corresponding to Area 1 to Area 4 shown in Fig. 4a1, illustrating the differences in spatially variant aberrations. The first row of Fig. 4a2, a3, the nuclear membrane and nucleolus indicated by the arrows appear blurred and less distinguishable (without aberration correction). These deviations in aberrations are not fully eliminated, resulting in decreased clarity when observing subcellular features. However, these structures are clearly visualized in the TI-AC results, as shown in the second row of Fig. 4a2, a3. Over time, the defocus distance of live cells may deviate from the initially set parameters for the defocus drive, thereby prohibiting accurate high-resolution QPI.
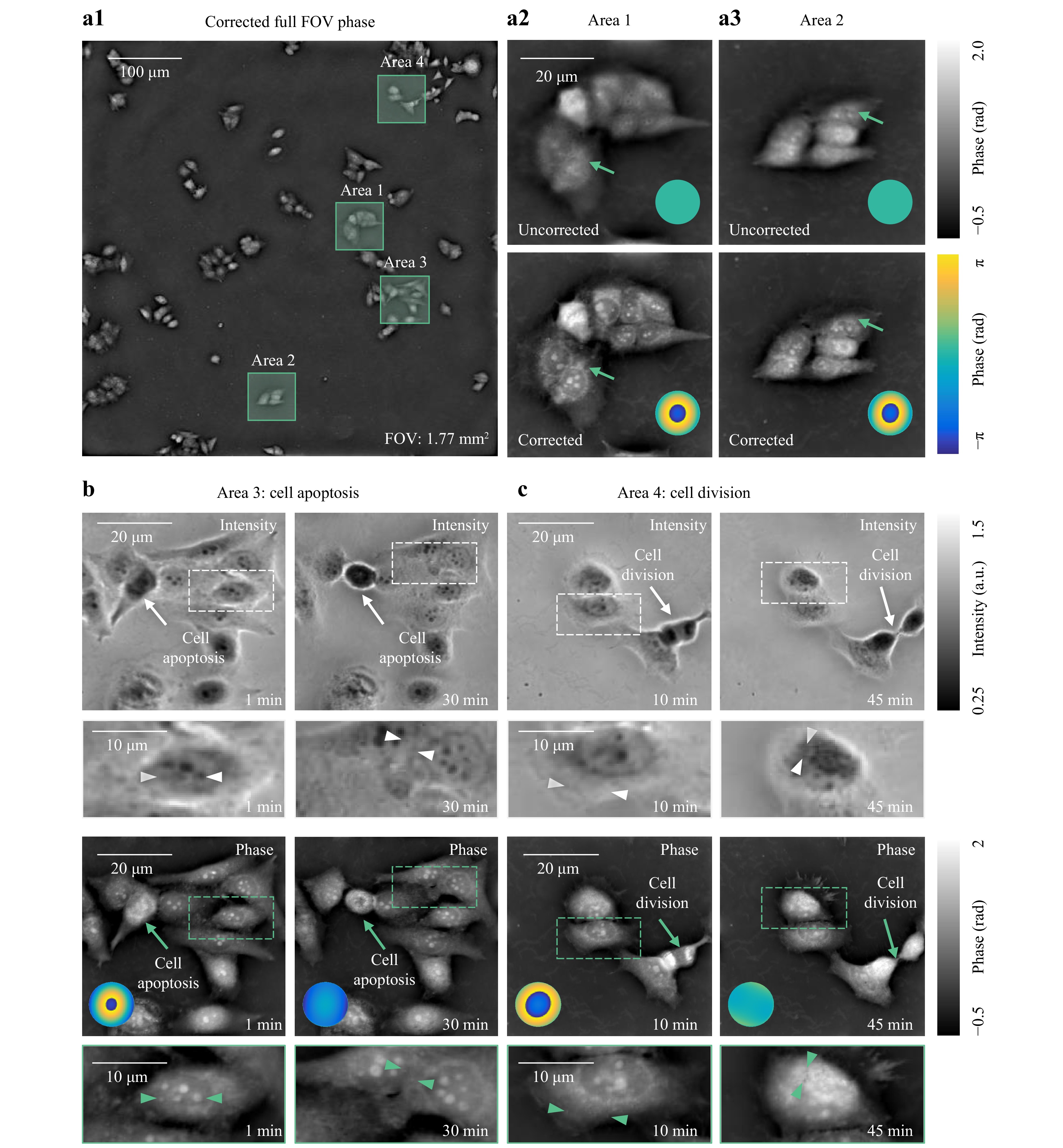
Fig. 4 Experimental results of live HeLa cells (Video S1). a1 Retrieved phase in the full FOV. a2 Enlarged view of Area 1 in a1. a3 Enlarged view of Area 2 in a1. b, c In-focus intensity (top), TI-AC-retrieved phase (bottom), and insets: phase aberration corresponding to Area 3 and 4 in a1.
In Fig. 4b, c, we further selected two cells (indicated by arrows) to study their morphology during apoptosis and division, which spanned over approximately 45 min. A timelapse movie created with one-phase reconstruction per 10 s is provided in Supplementary Video S1. Using the TI-AC method, it was possible to clearly observe apoptosis in Fig. 4b and cell division in Fig. 4c (see the cells indicated by the arrows) in live cells under a large FOV of 1.77 mm2, avoiding the inaccuracies caused by temporally varied aberration and focus drifts (see the insets phase aberration). It is noteworthy that in Fig. 4b, c, the long arrows indicate the life process the current cell is undergoing. The dashed rectangles represent the local magnification of cells with rich features, which allows for a clearer contrast between the intensity image and phase reconstructed by TI-AC. The short arrows can be used to indicate detailed features that are clearly displayed in the TI-AC-retrieved phase but are not visible in the intensity image, thereby emphasizing the pixel-super-resolution capability of our method. The unlabeled live HeLa cells experimental results revealed the capability of the TI-AC method to temporally correct varied aberrations and ensured imaging performance for long-term studies. In the experiments, in total, 12 intensity frames are acquired within a three-dimensional intensity set (2048 × 2048 × 12) for 12 axial z-slices under annular illumination within 0.18 s acquisition time (15 ms exposure time for each frame under 10× objective lens). On a normal laptop without GPU acceleration, the proposed method required ~ 65 s at 40 iterations for 12 intensity images in the experiments.
-
We proposed a TI-AC method for high-throughput transport-of-intensity QPI with aberration correction using LED annular NA-matched illumination. With its capability for aberration correction, TI-AC can eliminate the degradation effects caused by spatially non-uniform and time-varying aberrations, thus improving the imaging performance for long-term studies, such as live cell observations. The TI-AC method can achieve a 2× pixel super-resolution of the incoherent diffraction-limited imaging resolution using 12 through-focus intensity images. TI-AC expands TIE and enhances throughput by incorporating pixel super-resolution and adaptive aberration correction using partially coherent illumination to improve the signal-to-noise ratio in phase contrast. Unlike FPM’s need for precise NA-matched illumination, TI-AC offers flexibility by adapting to experimental constraints with a broader range of acceptable matching for annular illumination. More details on the comparison between AO-QPI and TI-AC can be found in Supporting Information, Comparison between AO-QPI and TI-AC. This could provide new possibilities for high imaging efficiency and accurate high-throughput capability in cell research and biomedicine, such as high-throughput plate reader systems in pharma industry for drug and toxicity screening. However, it is necessary to further reduce the input data to mitigate the negative impact of motion artifacts on the phase retrieval quality. Recently, deep learning has been successfully incorporated into computational optical imaging38-40, yielding less data requirements in QPI algorithms. Therefore, future studies should explore the use of deep learning for high-speed adaptive QPI under partially coherent illumination.
-
This study was supported by the National Natural Science Foundation of China (62227818, 62105151, 62175109, U21B2033, 62105156, 62361136588), National Key Research and Development Program of China (2022YFA120 5002), Leading Technology of Jiangsu Basic Research Plan (BK20192003), Youth Foundation of Jiangsu Province (BK20210338), Biomedical Competition Foundation of Jia-ngsu Province (BE2022847), Key National Industrial Technology Cooperation Foundation of Jiangsu Province (BZ2022039), Fundamental Research Funds for the Central Universities (30920032101, 30923010206), Fundamental Scientific Research Business Fee Funds for the Central Universities (2023102001), and Open Research Fund of Jiangsu Key Laboratory of Spectral Imaging & Intelligent Sense (JSGP202105, JSGP202201), National Science Center, Poland (2020/37/B/ST7/03629).








 DownLoad:
DownLoad: