-
Optical microscopy is a powerful tool for detecting subtle structures of samples, playing an irreplaceable role in many fields. However, traditional optical microscopy can only obtain the amplitude information of samples, and transparent samples, such as living cells cannot be investigated. Although fluorescence microscopy can selectively render and highlight the structures of interest by prior tagging with fluorescent markers, the phototoxicity and photobleaching of fluorescence tagging make it difficult to continuously observe living cells over a long time. Thus, there is an urgent need for label-free microscopic tools able to follow organelles in live cells. Digital holographic microscopy (DHM) 1-6, which combines digital holography and microscopy, is a label-free, quantitative phase microscopy approach. A typical setup for DHM is shown in Fig. 1a, in which a magnified object wave and a reference wave interfere with each other, and the generated off-axis hologram or phase-shifting holograms are recorded by a CCD camera. From the off-axis hologram (Fig. 1b), both the amplitude and phase images (Fig. 1c, d) of a sample can be obtained simultaneously. As an alternative, inline lensless DHM can help recover the phase information with an iterative algorithm without using an independent reference wave7, 8. Refocusing of the reconstructed images can further be performed digitally using the obtained complex amplitude of the object wave9, 10. In general, DHM can not only observe transparent samples with high endogenous contrast, but also quantitatively assess the thickness or refractive index distributions of these samples. Therefore, DHM has been widely applied in industrial inspection11, 12, visualization of liquid/gas flows13, biomedical imaging14, etc.
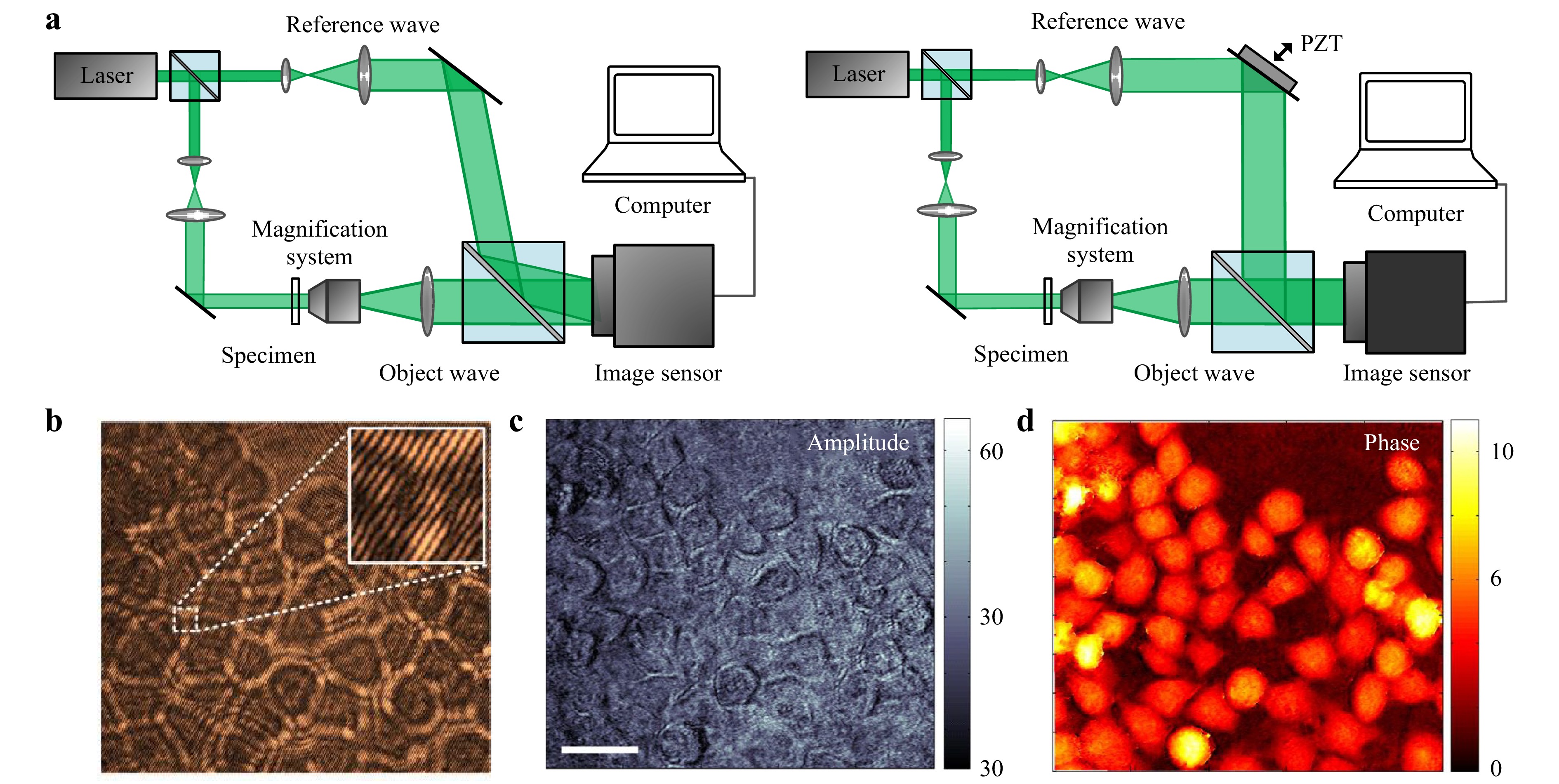
Fig. 1 Principle of digital holographic microscopy (DHM). a Schematic setup of off-axis (left) and in-line DHM (right). b Exemplary hologram of off-axis DHM. c, d Amplitude and phase images of HeLa cells reconstructed from b. Scale bar in c is adapted with permission from Ref. 76 ©The Optical Society.
The spatial resolution is of great importance for DHM because it determines the smallest structures that can be resolved. As illustrated in Fig. 2a, when two infinitely small points separated by a Rayleigh distance of 0.61λ/NA are imaged by a diffraction-limited imaging system, two Airy patterns are generated in the imaging plane, whose complex amplitudes are denoted as O1 and O2, respectively. Here, λ and NA indicate the illumination wavelength and the sum numerical aperture (NA) of the imaging system (NAimag) and illumination system (NAillum), respectively. For incoherent illumination, the intensity of the image is linearly related to the intensity emitted from the sample, that is, |O1|2+|O2|2. The two patterns are considered to be resolved if the center of the intensity pattern of O1 coincides with the first zero of the pattern of O2 (Fig. 2b). For coherent imaging (e.g., DHM), a linear relationship holds between the input complex amplitude and the output complex amplitude. In this case, the intensity of the image corresponds to |O1+O2|2, which is dependent on the phase difference Δ
$\varphi $ between O1 and O2. It is evident from Fig. 2c that for Δ$\varphi $ = 0 (in-phase), the Airy patterns of O1 and O2 are considered unresolved. However, for Δ$\varphi $ = π (anti-phase), the Airy patterns of O1 and O2 are well separated. To conclude, there is no easy criterion for evaluating the resolution of coherent microscopy (DHM), considering that the resolution depends on both the microscope and the phase of the sample. Nevertheless, we recommend the following: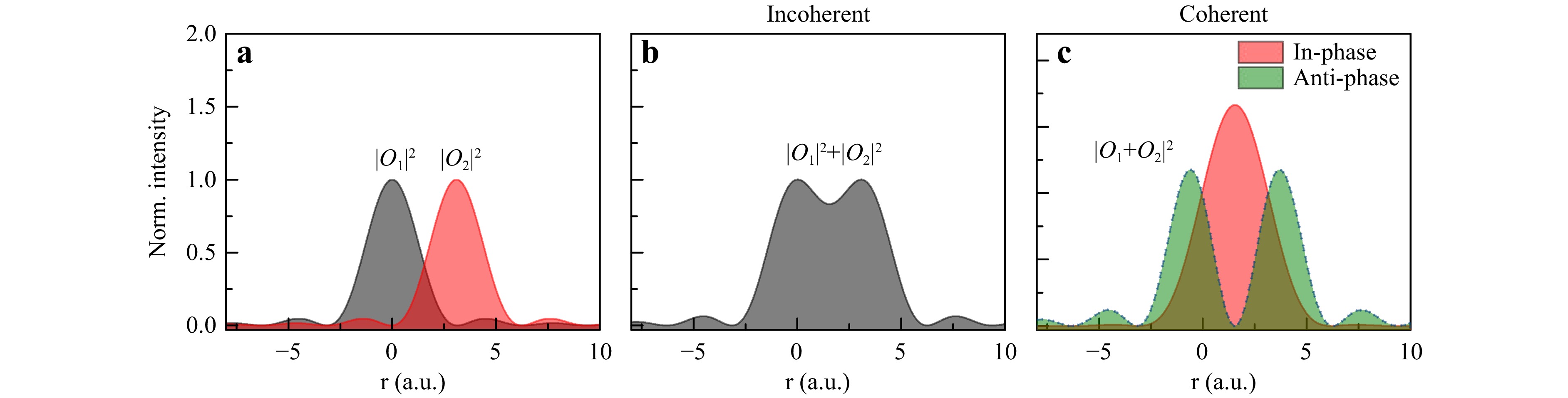
Fig. 2 Resolution criteria in incoherent and coherent systems. a Intensity distribution of the Airy patterns for the complex amplitude distributions, O1 and O2, obtained by imaging two infinitely small point sources through a diffraction-limited system; the superimposed intensities of O1 and O2 in incoherent microscopy b and coherent microscopy c. In-phase and anti-phase in c indicates that the cases O1 and O2 have a phase difference of 0 and π, respectively.
$$ \sigma =\frac{{\kappa }_{1}\lambda }{NA}=\frac{{\kappa }_{1}\lambda }{N{A}_{\rm{imag}}+N{A}_{\rm{illum}}} $$ (1) for evaluating the resolving power of optical microscopy. Factor κ1 is determined by the experimental parameters, such as the coherent noise level and the SNR of the detector, etc3, 15. Herein, we assign κ1 = 0.8216, 17, for which the principal intensity maximum of pattern O1 coincided with the first minimum of the in-phase O2. This suggests two options for enhancing the spatial resolution of the DHM. The first is the use of a shorter wavelength, for example, 193-nm18 light was used to enhance the spatial resolution of the DHM. The other is to enlarge the NAs of both the illumination and the recording systems.
In addition to the resolution, the field of view (FOV) is also a vital parameter of an imaging system. The ratio between these two parameters determines the space-bandwidth product (SBP) of the imaging system19, 20. Often, a DHM system has a limited SBP, and consequently, there is an inherent trade-off between resolution and FOV. This means that a reconstructed image with a higher resolution has a smaller FOV. Just as an example, a standard 20 × /0.4 microscope lens with a resolution limit of 0.8 μm and a circular FOV of 1.1 mm in diameter, provides a SBP of ~7 megapixels21. However, microscopists always expect to have a higher SBP in the sense of an increasing resolution while maintaining FOV. There are many degrees of freedom, including spatial/temporal resolution, FOV, polarization, spectrum, etc., in an imaging system. We can convert or trade some unused degrees of freedom (e.g., time) for an increase in SBP. In the past few decades, computational microscopy methods have emerged, generating images with high resolution and a wide FOV by using modulated illumination or applying other physical manipulations during the imaging process. By synthesizing apertures using the object information obtained under different modulation/manipulation operations, the SPB limitation of conventional microscopes (including DHM) can be bypassed22, 23.
This paper aims to review the resolution enhancement approaches of DHM, which are classified into three types: 1. Enlarging the NA of illumination via oblique illumination, structured illumination, and speckle illumination; 2. Enlarging the NA of the recording system via hologram extrapolation, hologram expansion, and pixel super-resolution. 3. Artificial intelligence (AI) assistance resolution enhancement approaches for DHM. This paper will cover the basic principles, implementation schemes, and exemplary results of the different approaches. We conclude by providing a summary and future outlook of resolution-enhancement approaches for DHM.
-
A microscopic imaging system is commonly introduced to DHM, which provides a magnified and high-resolution image of the sample. A plane wave is often used for illumination, and only the spatial frequencies diffracted by the sample up to ~ NAimag/λ can be transmitted through the limited aperture of the microscope lens (Fig. 3a, upper part), resulting in an upper limit for the spatial resolution in terms of 0.82λ/NAimag. Therefore, using oblique illumination, structured illumination, or speckle illumination to provide a NAillum is an effective method for further improving the resolution.
-
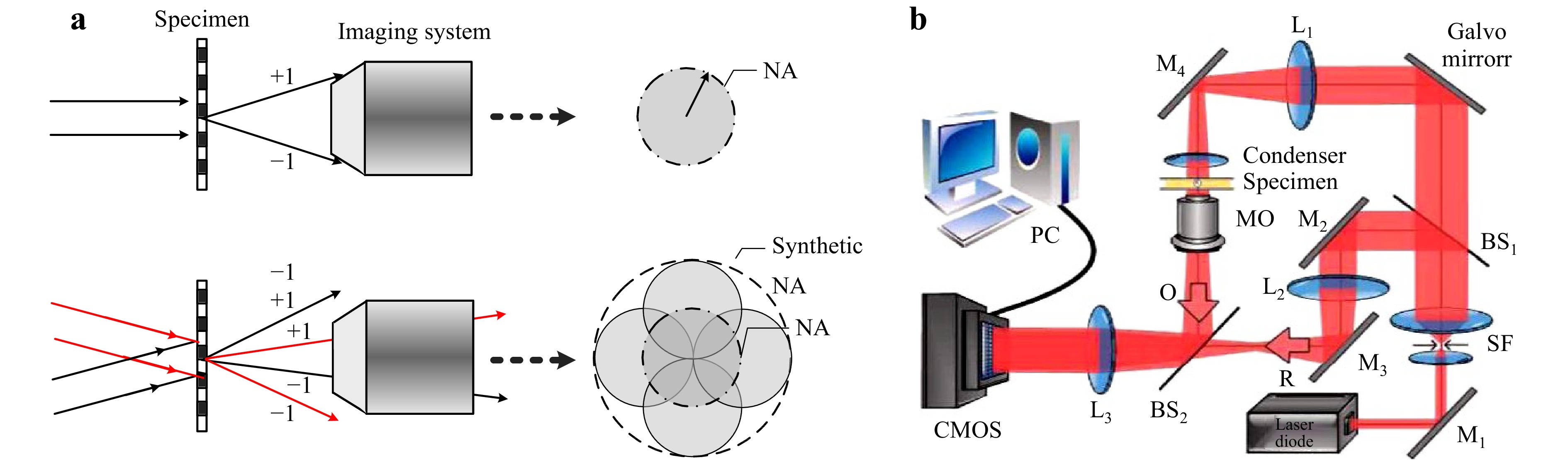
Since the first implementations of oblique beam illumination in DHM in the 1970s24-27, many approaches have been extensively reported on for replicating a larger aperture28-48. When a sample is illuminated by an oblique wave, the high spatial frequency of the object wave in the opposite direction of the oblique illumination will be downshifted and, thus, will pass through the limited aperture of the imaging system (Fig. 3a, lower part). The downshifted frequencies are back-assembled to their original positions in the spectrum of the object, thus, synthesizing a wider spectrum than that of the NA-defined aperture31. The final resolution-enhanced image is obtained by an inverse Fourier transform (FT) of the synthesized spectrum. In comparison with conventional lens-based DHM with a resolution limit of 0.82λ/NA, DHM with oblique beam illumination has an enhanced spatial resolution, as described in Eq. 1.
Kuznetsova et al. and Schwarz et al. used oblique beam illumination to downshift the high-frequency components of the spectrum of the object, and introduced a conjugate carrier phase to upshift the spectrum content back to its proper region28, 50. This process was repeated sequentially for both the x- and y-illumination directions, thus allowing for the transmission of extended frequency bandwidths of the 2D object, yielding a resolution gain with a factor of three. Mico et al. utilized a vertical-cavity surface-emitting laser (VCSEL) array to generate multi-directional oblique illumination of DHM and retained a resolution gain with a factor of five47. The use of scanning elements has also been reported as a technological improvement for providing more flexible oblique beam illumination28, 33, 37, 51, which has also been validated29, 31, 52 in comparison with the tilting of the illumination direction. For instance, Cheng et al. used a 2D Galvo-scanner to generate oblique illumination for DHM (Fig. 3b), achieving a two-fold isotropic resolution enhancement. 49 Oblique beam illumination for resolution enhancement has also been implemented using a spatial light modulator (SLM) 53-55 or a fiber bunch56-60. Meanwhile, single-shot synthetic aperture DHM was realized by using an SLM to generate multiple non-coplanar illumination beams, and using coherence gating to avoid self-interference between these non-coplanar beams53. Moreover, wavelength multiplexing techniques34-36 were utilized to perform multiple oblique illuminations during a single exposure. Oblique beam illumination techniques have recently been implemented in a commercial upright Olympus microscope39. Notably, the maximum synthetic numerical aperture is limited by NA<1 in imaging systems with dry objectives, and further resolution improvements to λ/3.7 were demonstrated using evanescent waves29. In addition, axial rather than transversal resolution improvement has also been validated by SA generation61, and an application of the technique to edge processing was also reported62. It is interesting to mention that oblique illumination has also been applied to differential interference contrast (DIC) microscopy63 and Zernike phase contrast microscopy64.
Recently, oblique illumination was also applied to obtain 3D refractive index (RI) tomographic images of transparent or translucent samples via optical diffraction tomography (ODT)49, 65. ODT enables the probing of 3-D RI maps of a sample by recording the complex wavefront diffracted while rotating the sample66, 67 or varying illumination angles68, 69. Kim68 adapted DHM to ODT by using a 2D galvanometric mirror to generate different illumination directions and consequently, reconstructed a 3D RI distribution of the samples with high lateral and axial resolutions. Ozcan70 presented an on-chip ODT scheme that enables the imaging of a large volume of approximately 15 mm3, with a spatial resolution of < 1 μm ×1 μm × 3 μm. In 2020, Wang et al.71 reported a mechanical-scanning-free ODT configuration using self-accelerating Airy beams that are tilted along the beam path direction, providing a 3D volumetric view of the cells. Recently, Kus et al.72 proposed a real-time ODT system for recording a complete set of projections in a single hologram in a multiplexing manner by using a microlens, with which the tomographic images of living cells and flow cytometry could be observed clearly. In addition to advances in ODT hardware, artificial intelligence (AI)-based reconstruction algorithms have been reported to reduce the recording time and improve the quality of the reconstructed images73.
-
Structured illumination microscopy (SIM) is a super-resolution optical microscopy technique that has the merits of being fast, minimally invasive, and has no requirement for fluorescent labeling74, 75. Compared with conventional wide-field (WF) microscopy, SIM provides two-fold spatial resolution enhancement by illuminating the sample with a periodic pattern and recording the generated moiré pattern. Because of the moiré effect, the high spatial frequency components of the sample, which are not accessible in conventional microscopy, are shifted into the detectable domain and thus can be observed. However, the application of SIM has been limited to fluorescent samples. In 2010, Mudassar and Hussain60 applied it to non-fluorescent scattering imaging, for which fringe patterns were generated by the interference between the beams carried by two fibers.
A DHM with structured illumination generated by an electric modulation device has been proposed. The fringe patterns were generated by a spatial light modulator (SLM)76 in 2013 and by a digital micromirror device (DMD)77 in 2015, whereby fringes with different orientations and phase shifts were projected without mechanical motion. In the implementation, four binary phase gratings rotated by m×45° (Fig. 4a) and generated by an SLM or a DMD are projected onto the sample, so that the sample is illuminated sequentially by four sinusoidal fringe patterns. After passing through a telescope system comprised of the microscope objective MO and lens L, the object wave interferes with a tilted reference wave R, and the generated holograms are recorded by a CCD camera, as shown in Fig. 4b. We denote with Ψmn the object wave generated by illuminating the sample with the grating as having the m-th orientation and n-th phase shifting. Thus, the recorded hologram can be described as Imn = |R+ Ψmn|2. From this intensity, the wave Ψmn can be reconstructed using standard reconstruction methods, as in off-axis DHM. Generally, Ψmn can be decomposed into three components, Am, −1, Am, 0, and Am,1 corresponding to the −1st, 0th, and +1st diffraction orders of the illumination wave. When we assume that the phase shift increment for each shifting of the grating is α, Ψmn can be written as:
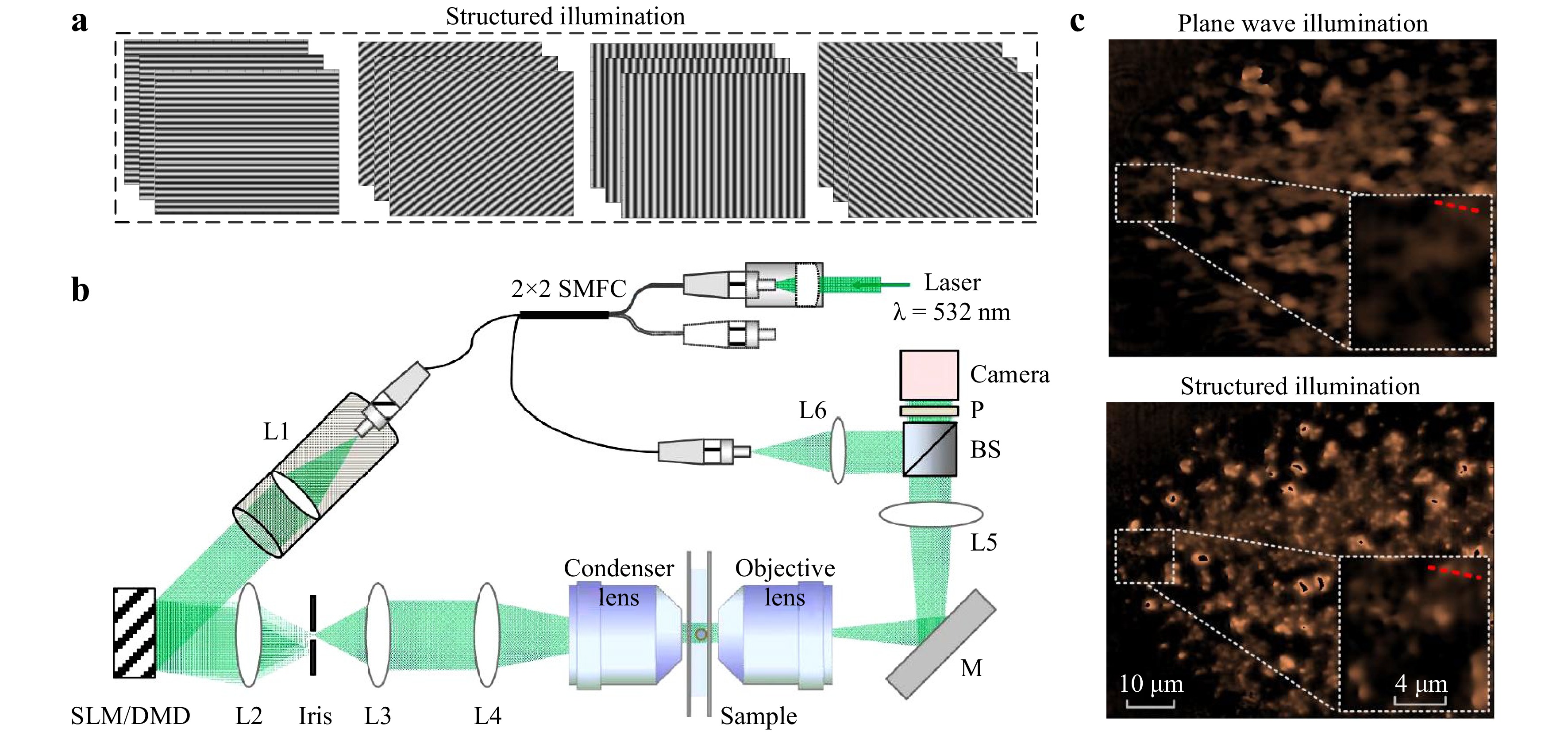
Fig. 4 DHM with structured illumination. a Schematic of structured illumination with different orientations and phase shifts. b Schematic setup of DHM with structured illumination. c Experimental results for resolution enhancement. Reconstructed phase images using plane wave illumination (top) and structured illumination (bottom). b is adopted from Ref. 77. and c is adopted from Ref. 76.
$$ {\Psi }_{mn}={\gamma }_{-1}\mathrm{exp}(-in\alpha ){A}_{m,-1}+{\gamma }_{0}{A}_{m,0}+{\gamma }_{1}\mathrm{exp}(in\alpha ){A}_{m,1} $$ (2) where γ−1, γ0, and γ1 denote the magnitudes of the diffraction orders. From Eq. 2, we can calculate the reconstructed object waves Am, −1, Am,0, and Am,1 from the different diffraction orders:
$$ \left[\begin{array}{c}{A}_{m,-1}\\ {A}_{m,0}\\ {A}_{m,1}\end{array}\right]={\left[\begin{array}{ccc}{\gamma }_{-1}\mathrm{exp}(-i\alpha )& {\gamma }_{0}& {\gamma }_{1}\mathrm{exp}(i\alpha )\\ {\gamma }_{-1}\mathrm{exp}(-i2\alpha )& {\gamma }_{0}& {\gamma }_{1}\mathrm{exp}(i2\alpha )\\ {\gamma }_{-1}\mathrm{exp}(-i3\alpha )& {\gamma }_{0}& {\gamma }_{1}\mathrm{exp}(i3\alpha )\end{array}\right]}^{-1}\cdot \left[\begin{array}{c}{\Psi }_{m1}\\ {\Psi }_{m2}\\ {\Psi }_{m3}\end{array}\right] $$ (3) Then, Am,-1 and Am,1 under each illumination direction are compensated for by the carrier phase due to the tilted propagation direction along the ±1st diffraction orders, and synthesized together with Am,0 in the Fourier plane to yield the synthetic spectrum. Finally, a focused image with enhanced resolution was retrieved by the inverse FT of the synthetic spectrum. Assuming that the angular aperture of the imaging system is NAimag, the synthetic NA of the SI DHM is NA = NAimag+sinθillum. Here, θillum denotes the illumination angle of the +1 or −1 diffraction orders, and the highest value of the sinθillum is, in turn, determined by the NA of the condenser lens. Fig. 4c validates the resolution enhancement of the structured illumination in comparison with on-axis illumination. Of note, the phase image at the bottom (obtained with structured illumination) has a better resolution compared with that on the top, and the two particles separated by 1.4 μm became distinguishable.
Recently, structured illumination has been widely applied to different variations of DHM for the purpose of imaging transparent samples with resolution enhancement76-89. SI-based DHM was extended for resolution enhancement in the axial direction, aside from the lateral directions90. An iterative reconstruction algorithm, as well as a PCA-based algorithm, were employed to obtain resolution-enhanced images using structured illumination with unknown phase shifts or free of phase shifts82-84, 89. In 2021, an end-to-end deep-learning-based method, DL-SI-DHM, was proposed for improving the reconstruction efficiency and accuracy of SI-DHM91. In addition to synthetic-aperture phase imaging, Shin et al. in 2015 and Chowdhury et al. in 2017 utilized DMD- and SLM-based structured illumination to obtain 3D refractive index tomographic images of samples77, 92.
-
Speckle illumination has been known since the invention of the laser in 196093. Speckle illumination often reduces the signal-to-noise ratio (SNR) in coherent imaging. Speckle fields can be understood as a combination of plane waves with various random illumination directions. These oblique plane waves shift the spectrum of the object in the reciprocal plane, allowing for access to additional spatial frequencies. Thus, speckles can be used to enhance the spatial resolution and reduce the coherent noise in DHM or other coherent imaging37, 94-97.
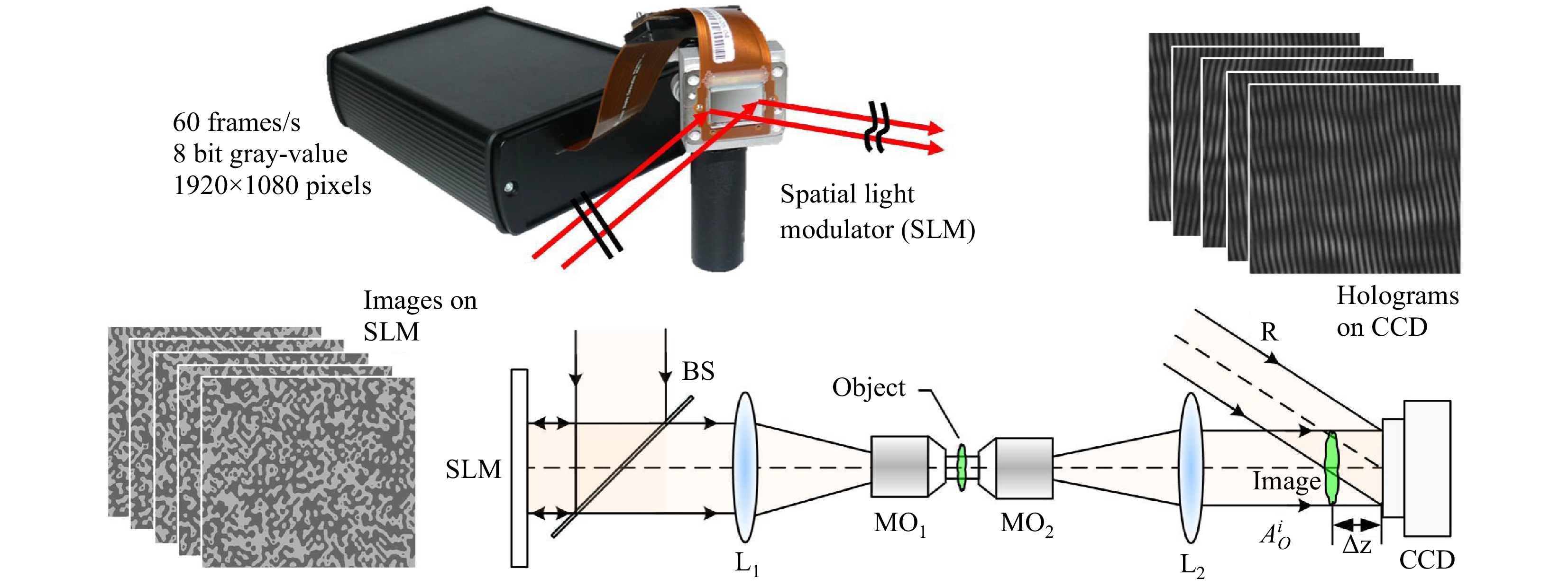
Fig. 5 shows the optical setup of DHM with a speckle illumination according to Ref. 95. The speckle field was generated by an SLM and projected using a telescopic system L1-MO1 in the sample plane, where
$ {A}_{Speckle}^{i} $ is the ith speckle illumination and$ {A}_{o}^{i} $ refers to the complex amplitudes of the object wave when the sample was illuminated with$ {A}_{Speckle}^{i} $ . When$ {A}_{o}^{i} $ interferes with a reference wave R, the hologram can be denoted as$ {I}_{o}^{i}={{|A}_{o}^{i}+R|}^{2} $ . The complex amplitude of the speckle field$ {A}_{Speckle}^{i} $ can be reconstructed from the hologram recorded in the absence of a sample. Often, the holographic resolution-enhanced image can be obtained by averaging multiple angle-dependent E-field images Oave =$ 1/\mathrm{N}· \sum _{i=1}^{N}{{A}_{o}^{i}/A}_{Speckle}^{i} $ 96. It is worth mentioning that the resolution enhancement capability of such an averaging operation will be lower when the speckle field has an unequal weight or power over the entire frequency spectrum.To overcome this limitation, an iterative reconstruction method95 was proposed for synthesizing a larger NA. The key idea of the iteration is to propagate the object wave between the image plane and the CCD plane, updating the speckle illumination in the image plane and the object wave intensity (with the recorded one) in the CCD plane. The iterative method enhances not only the resolution but also the SNR when the reconstructed object wavefronts from different speckle-based holograms are averaged. Utilizing SLM for speckle field illumination avoids mechanical movements and allows for a high repeatability in comparison with dynamic devices. Time-changing speckle illumination is similar to structured illumination. The concept in common is the encoding of an object with an a priori known high-resolution pattern that folds the high spatial frequencies into the low bandwidth range. The decoding patterns should be matched to the time-changing encoding patterns.
Similar to speckle illumination, a scattering medium can also be placed before the sample to enhance the spatial resolution and FOV98, 99. Multiple scattering of the medium is a deterministic process that is described by a transmission matrix (TM) in transmission geometry. TM-based imaging has been introduced in DHM, yielding an improved resolution beyond what an objective-lens-based imaging system can achieve99. Similarly, a single multimode optical fiber was demonstrated for scanner-free and wide-field endoscopic imaging96. Beyond resolution enhancement, Baek et al. demonstrated in 2018 that a high-resolution, long working distance, reference-free DHM can be performed by using a scattering layer to replace the conventional imaging lens100. By exploiting the randomness of a multiple-scattering layer, it allows for holographic imaging of a microscopic object without introducing a reference beam. The authors experimentally demonstrated a high NA (0.7) with a working distance of 13 mm.
-
Compared to DHM with an imaging system, DHM without using an imaging lens (lens-free DHM) possesses three significant advantages. The first aspect is its compactness and low-cost because it does not employ an objective. The second is a large FOV. The third is the high compatibility and ease of integration with microfluidic and on-chip devices. In the following sections, we review the resolution enhancement of lens-free DHM via hologram extrapolation, hologram synthesis, and pixel super-resolution techniques.
-
As a major type of lens-free DHM, lensless DHM can be traced back to an inline architecture proposed by Gabor8. In Gabor, in lensless DHM8, 101, 102 (Fig. 6a) a sample is illuminated by a spherical wave. The wave diffracted by the sample interferes with the non-diffracted wave, which also acts as a reference wave. Direct reconstruction of the generated hologram suffers from overlapping of the DC term and the twin image. Iterative approaches7, 103, 104, and compressive sensing105 have been invented to retrieve phase information from an oversampled diffraction pattern. The achievable spatial resolution is believed to be limited by the size of the hologram8, 104:
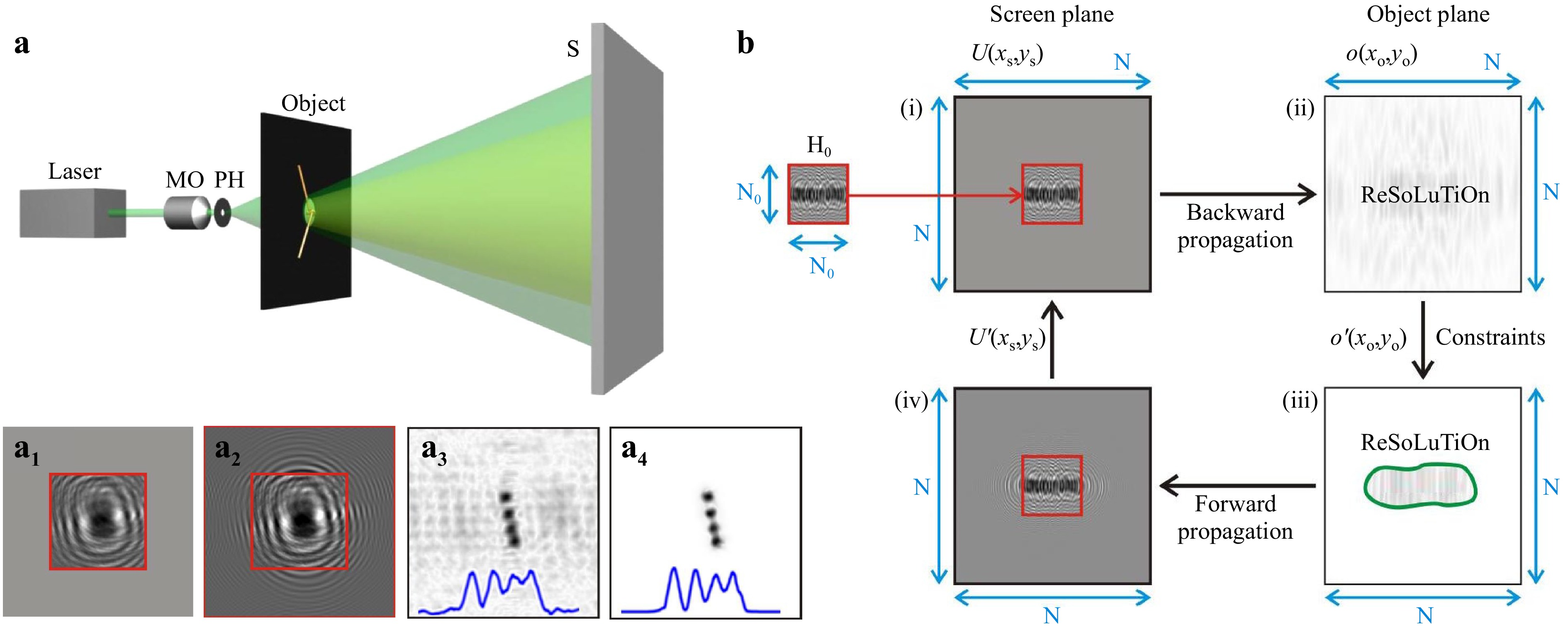
Fig. 6 Resolution enhancement of lensless DHM by self-extrapolation of holograms. a Experimental setup and results. a1, hologram with zero-padding. a2, hologram after 100 iterations. a3 and a4 refer to the reconstructed image without and with self-extrapolation, respectively. b Illustration of iterative reconstruction of a hologram by self-extrapolation. The image is adopted from Ref. 104.
$$ \sigma =\frac{\lambda \text{z}}{N{\Delta }_{S}} $$ (4) where λ is the wavelength, z is the distance between the object and the screen, N is the number of pixels, and ΔS is the pixel size of the detector. In 2013, resolution enhancement of lensless DHM was reported by extrapolation of the hologram104,, and later, this method was applied to terahertz inline lensless holography106, 107. The flowchart of the resolution enhancement routine is shown in Fig. 6b, and includes the following steps:
(1) Initialize the object wave U(xS, yS) in the hologram plane by taking the square root of the hologram intensity H0 of N0×N0 and padding it with zeros to a matrix of N × N with N > N0 (see Fig. 6a1). In contrast, random noise can be added to the padded area.
(2) Propagate the padded wave U(xS, yS) to the object plane by using the propagation integral7, yielding o(xo, yo).
(3) In the object plane, a constraint concerning the finite size and positive absorption of the sample is applied to o(xo, yo), resulting in
$ {o}^{\text{'}} $ (xo, yo).(4) Propagate
$ {o}^{\text{'}} $ (xo, yo) in the hologram plane and replace the amplitude of$ {o}^{\text{'}} $ (xo, yo) with the square root of the hologram intensity H0 within the central N0×N0 area (see Fig. 6a2).Once the above procedures have been repeated over 500 iterations, the complex amplitude of the object wave can be retrieved, which has a resolution of σ = λz/(NΔS) instead of λz/(N0ΔS). It is clear that the image reconstructed with hologram extrapolation (Fig. 6a4) has finer structures than that obtained without using self-extrapolation (Fig. 6a3). Quantitatively, the resolution was enhanced from 5.9 μm to 1.8 μm by padding a hologram with 300 × 300 to 1000 × 1000 pixels108. The reason for the resolution enhancement by hologram extrapolation is that the hologram itself contains a series of wavelets constituting the wavefront, which can be fitted better through extrapolation and yield a larger effective hologram104. This hypothesis is confirmed by a closer look at the intensity distributions ((iv) in Fig. 6a2) in the hologram plane.
-
In addition to inline lensless DHM, DHM, which records the interference between an object wave and an independent reference wave can reconstruct the phase of a sample free of twin-image disturbances. Fig. 7a shows a standard lens-free DHM configuration using an independent reference wave109, 110. Fig. 7b shows a modified lensless DHM configuration by the insertion of an SLM into the classical Gabor architecture102. The SLM is used to perform phase shifting of the DC term of the object wave. The complex amplitude distribution of the object wave passing through a sample can be recovered using a standard phase-shifting reconstruction algorithm. For the two types of lens-free DHM configurations (with and without an independent reference wave), the spatial resolution is limited by the size of the hologram, as shown in Eq. 4. In 2002, resolution enhancement of lens-free DHM was first demonstrated111 by generating an expanded hologram with multiple sub-holograms. Each sub-hologram covers a different frequency spectrum of the input object. When the reconstructed image of each hologram is synthesized, an image with an enlarged FOV and an enhanced spatial resolution can be obtained109, 110. Generally, hologram synthesis of lens-free DHM can be performed shifting the digital camera109 or sample110, 112, using oblique beam illuminations113, or inserting a diffraction grating between the object and digital camera114,115. The above-mentioned three strategies are equivalent and generate the same output, which is a larger synthetic hologram that contains a larger sample spectrum.
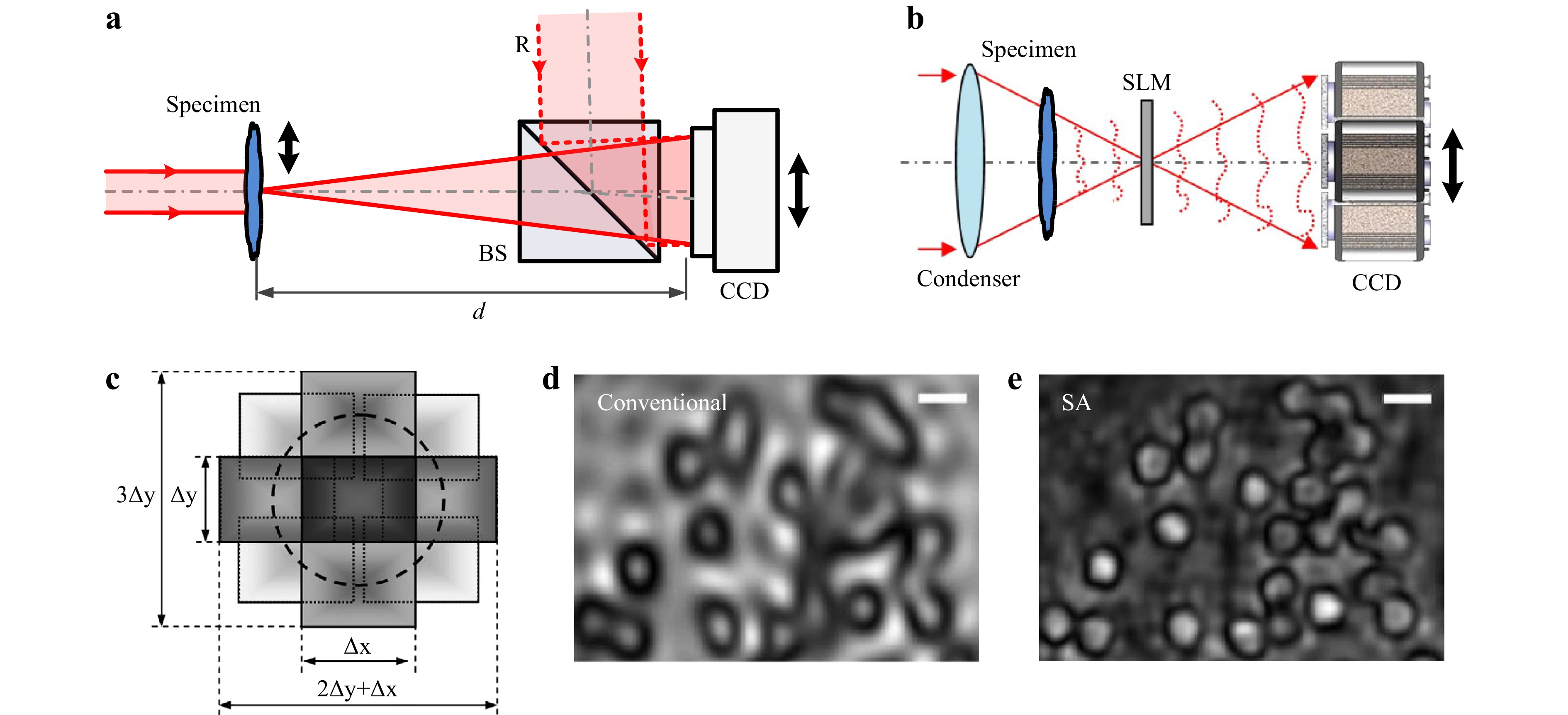
Fig. 7 Resolution enhancement of DHM via synthesizing a larger hologram. a Synthetic aperture of lens-free DHM using an independent reference wave. b Synthetic aperture of lensless DHM102, reproduced with permission © IOP Publishing. c Synthesized frequency spectrum. d and e, Images of blood cells without and with applying synthetic aperture, respectively. The images in (c−e) are adapted from Ref. 113 ©The Optical Society.
Figs. 7c−e show the experimental results of the lens-free DHM based on hologram synthesis. The synthesized spectrum is shown in Fig. 7c, and the resolution-enhanced image (Fig. 7e) can be obtained from the Fourier transform of the synthesized spectrum. It is clear that the SA image of the blood cells in Fig. 7e has much finer structures than that in the conventional image in Fig. 7d. Furthermore, it was found that the hologram synthesis enhanced the effective NA from 0.13 to 0.75.
-
The architecture of a standard on-chip DHM116-119 is shown in Fig. 8a. A partially coherent light source is used for illumination, usually at > 2–3 cm (z1 distance) above the sample. A semi-transparent sample is placed on top of an image sensor with a typical spacing of < 1 mm (z2 distance). As a result, the sample casts an inline hologram, which is directly recorded by a CMOS or CCD image sensor, without using any imaging lenses. The magnification time of the on-chip DHM is defined as M = (z1 + z2)/z1. For z1 much larger than z2, the magnification is approximately 1. The hologram recorded in the on-chip DHM is an in-line hologram (Gabor). The direct reconstruction of object-related holographic information from an inline hologram is often obscured by the twin image and the DC term. Phase retrieval approaches using an iterative approach7 or additional constraints, such as multiple measurements at different heights120-123 or illumination angles124, can be employed to eliminate twin image noise. There are several factors that can limit the resolution of on-chip DHM, including diffraction, pixel size, image chip area, and coherence of the light source. In practice, the primary limitation of lens-free on-chip DHM resolution comes from the pixel size of the sensor (typically 1–2 μm).
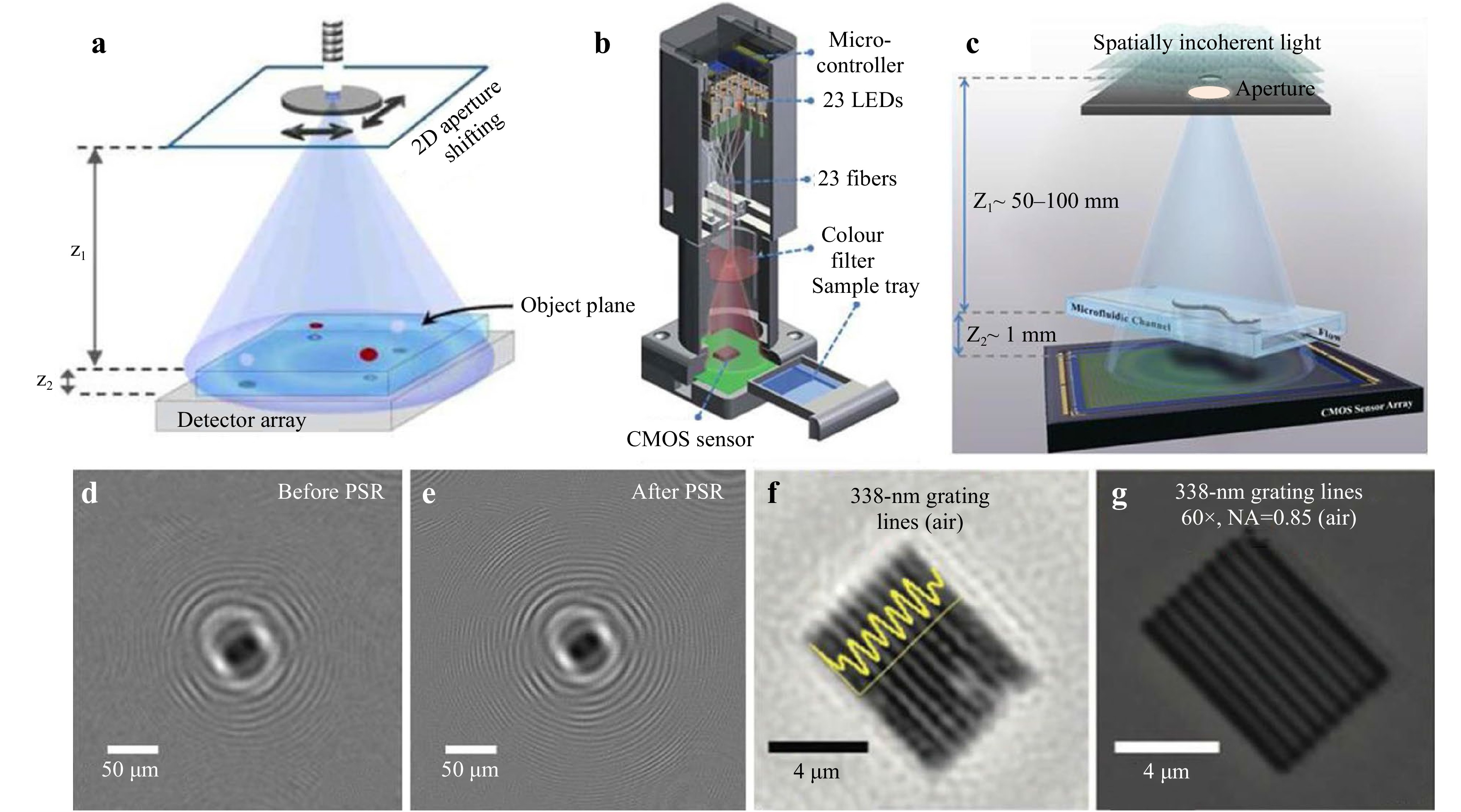
Fig. 8 Pixel super-resolution (PSR) for on-chip lensless DHM. Subpixel shifts in a digital hologram can be achieved through a source shifting, b an array of static light sources, e.g., fiber-coupled LEDs that are individually controllable, sensor shifting, or c sample shifting using e.g., a micro-fluidic flow. d An in-line hologram before PSR. e Pixel super-resolved hologram of the same object. f Reconstructed image of the grating with 338 nm line-width using PSR. g Microscope comparison of the same region of interest. The image is adopted from Ref. 118.
To improve the resolution of on-chip DHM, pixel super-resolution (Pixel SR)125, 126 can be adopted by shifting the hologram along the x- and y-directions in subpixel increments. The relative lateral shift of the hologram with respect to the sensor array can also be performed via shifting of the image sensor127, the illumination source128 (Fig. 8a, b), or the sample129 (Fig. 8c), respectively. A low-resolution hologram is captured at each location of the shifted grid. Then, using multiple LR holograms, a higher-resolution hologram can be digitally synthesized by using a “shift-and-add” algorithm, in which the low-resolution (LR) holograms are upsampled, shifted, and digitally added. Alternatively, iterative methods can be used to upsample a high-resolution image from a series of low-resolution images. For this purpose, a cost function can be used for optimization125:
$$ {x}^{*}=\mathrm{arg}\mathrm{min}{{\displaystyle \sum _{i}\Vert {W}_{i}\cdot x-{y}_{i}\Vert _{p}^{q}}}+\alpha \gamma (x) $$ (5) This equation contains two operations, namely, norm and regulation, where i represents the recording times. yi is a low-resolution hologram, and x is the desired high-resolution image. Wi represents the digital processes of shifting and down-sampling of an image. This synthesis method is equivalent to recording holograms with smaller pixel sizes and higher spatial density detectors. The second part γ(x) is a regularization parameter to maintain/regulate the desired quality in the reconstructed image. By solving this optimization function, an image with a pixel size smaller than that of the digital camera can be obtained by synthesizing a series of sub-pixel-shifted LR images. A comparison of Fig. 8d, e shows that PSR can provide a more refined hologram with high-frequency fringes. PSR yields a high-resolution image (Fig. 8f) of a grating (line-width ~300 nm), whose resolution is equivalent to an effective NA~0.9, as shown in Fig. 8g116. Using the PSR techniques, sub-micrometer resolution over a wide FOV of 20–30 mm2 can be obtained, providing gigapixel throughput with a simple, compact on-chip DHM design130, 131.
Instead of physically moving the image sensor, the light source, or the sample, virtual pinhole scanning completed by deconvolving a hologram with the measured PSF is an alternative way to improve the resolution of an on-chip DHM with an extended light source132. PSR can also be performed by varying the propagation distances (i.e., z2)133, or by varying the illumination wavelengths in small increments (e.g., 2–3 nm)134. To further speed up the sub-hologram recording process by varying the illumination wavelength, color LR holograms can be recorded, where the holograms of the red, reen, and blue illuminations are multiplexed using a sub-pixel shifted Bayer color filter array119. Considering that PSR can only enhance the effective NA of the on-chip DHM to 0.9, a synthetic aperture-based on-chip microscope with which the illumination angle is scanned across the surface of a dome (from −50° to 50°) was proposed, which further increased the effective NA to 1.4, achieving a 250-nm resolution at a wavelength of 700-nm across the very large FOV of 20.5 mm2124.
Theoretically, an effective NA of 1+n can be achieved in a lensless on-chip DHM using the PSR/SA approach, assuming that the medium between the source and the sample planes is air. Here, n denotes the refractive index of the medium that fills the space between the sample and sensor planes. However, none of these techniques can be considered to exceed the diffraction limit of light, as they are entirely based on propagating waves that result from coherent light-matter interactions.
-
Deep-learning135, 136 has been demonstrated as being a powerful tool for solving various inverse problems by training a network with a large quantity of paired images. Deep learning can map the relationship between the input and target output distributions without any prior knowledge of the imaging model. Deep learning has been widely used for holographic image reconstruction137-139, auto-focusing140, 141, and resolution enhancement142, 143.
The deep-learning configuration for the resolution enhancement of DHM is shown in Fig. 9. By training a set of matched LR and high-resolution images, the relationships between them can be learned. Thus, a high resolution can be retrieved from one or multiple low-resolution images captured by a similar setup. The establishment of the mapping function between the high-resolution output image and the LR input images is called the objective function and is expressed as follows:
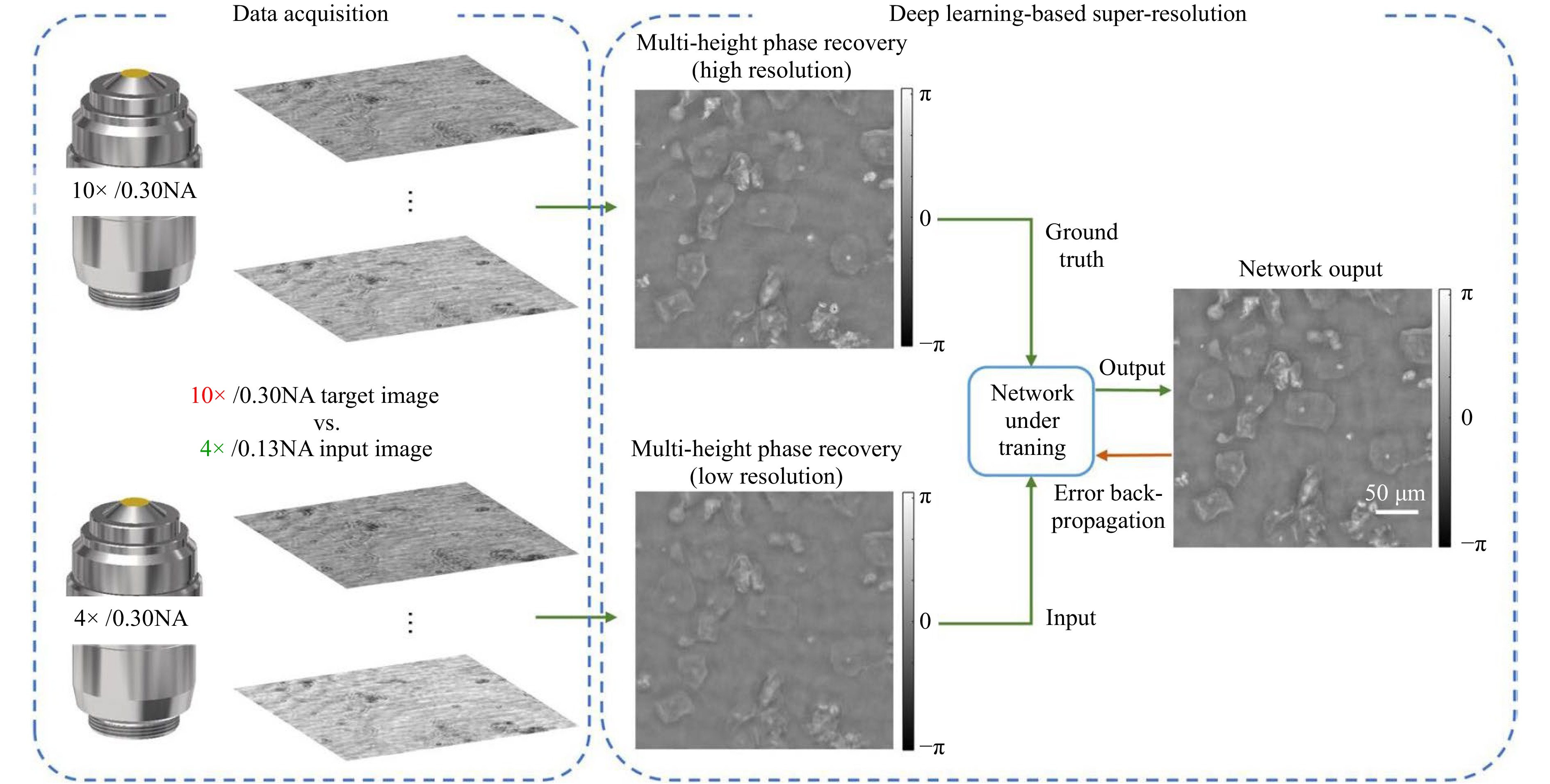
Fig. 9 Schematics of the deep-learning based method for resolution enhancement of DHM. Images were taken from Ref. 144.
$$ {R}_{\text{learn}}\text=\underset{{R}_{\theta },\theta \in \Theta }{\mathrm{arg}\mathrm{min}}{\displaystyle \sum _{n=1}^{N}F\left[{x}_{n},{R}_{\theta }\left({y}_{n}\right)\right]}+g(\theta ) $$ (6) where Rlearn is the optimal solution of the weight parameter of the network, x and y are the training set, F145 is the loss function for appropriate error metrics, and g(θ) is a regularization term for the parameter θ to avoid overfitting146. By continuously adjusting θ, the error between the output Rθ(yn) of the neural network and the target image xn is minimized. Therefore, as long as the establishment of the model is completed through data statistics, it can be applied to solve inverse problems in imaging. Using the network described in Eq. 6, deep learning has also been used to enhance the resolution of data-driven models for the following two systems: (1) lensless DHM and (2) lens-based DHM systems.
In the first case, a deep learning algorithm based on a generative adversarial network (GAN) must be used in an on-chip lensless DHM to achieve sub-pixel resolution147. In this method, the LR reconstructed images are used as inputs and the corresponding high-resolution images of different samples obtained by the “shift-and-add” approach are used as the labels for training the network. A well-trained framework can generate high-resolution images from unseen LR data without an iterative engine and prior knowledge of the system. In 2019, Liu et al. demonstrated that a resolution-improved image could be obtained from much fewer (e.g., 1 or 4 instead of 36 in conventional Pixel SR algorithm) low-resolution sub-pixel-shifted images of the same object by using a neural network, which significantly reduced both the number of hologram measurements and the computation time necessary for reconstruction144.
The network training process for the lens-based microscopic imaging system is shown in Fig. 8. The reconstructed images of the holograms obtained under the low-magnification objective were used as inputs, and the counterparts obtained under the high-magnification objective were used as labels in the network to generate an image with a resolution of the high-magnification objective, but with the same FOV as of the low-magnification objective 144. In this way, the diffraction limit defined by the NA of the objective and the SBP of the system can be broken, so that the holographic reconstruction image has a higher resolution and the reconstruction efficiency is improved as compared with the iterative process for each image. A deep-learning-based upscaling method was proposed for overcoming the trade-off between a large FOV and a high resolution, yielding an enlarged hologram with a smaller effective pixel size (enhanced sample details), for which inline holograms are used as training material for the convolutional neural network148. In this method, the deep-learning method only uses a single image obtained with a low-NA objective for magnification, allowing detailed analysis of a sample with a high resolution and a large FOV. However, considering that LR-input images do not contain high-resolution components physically, the resolution enhancement capability (or the right guessing of unknown details) of the network is limited by the adequacy of the training data149. As a remedy, people tend to integrate deep-learning-based strategies and illumination-modulation techniques to enhance the resolution of DHM. For instance, in 2021, Meng et al. demonstrated that the deep-learning algorithm simplifies91 not only the resolution-enhanced reconstruction process of SI-DHM but also minimizes the recording requirements91.
In general, for both lensless DHM and lens-based DHM, a deep-learning-based framework can enlarge the SBP of coherent imaging systems using image data and convolutional neural networks, and provides a rapid, non-iterative method for solving inverse image reconstruction or enhancement problems in optics. Furthermore, it has a faster imaging efficiency, even with little prior knowledge147, and can reconstruct in real time150. This is because deep-learning methods use large-scale datasets to impose potential constraints on the resolution enhancement problem. A neural network has learned millions of weight parameters from a large amount of training data. These parameters can establish a high-dimensional nonlinear relationship between the input and output, which is difficult to express through simple formulas. Although classical principled algorithms are often outperformed by deep learning models, they also retain key advantages. First, classical algorithms inherently produce outputs that are consistent with their inputs because they rely exclusively on the underlying physics and principles formulated. Second, classic algorithms can be generalized for any valid measurement because they are not limited by the adequacy of the training data. Third, classic algorithms, in contrast to deep learning models, do not produce widely erratic outputs after minute tweaks to their inputs.149. In light of the above analysis, it is our opinion that deep learning results cannot be blindly trusted, something certainly true of any singular piece of evidence. Incorporating physical models into deep neural networks provides a new idea for expanding the generality and reliability of imaging151, which should be a new trend in deep learning-based resolution enhancement.
-
In this review, we summarize resolution enhancement approaches for digital holographic microscopy (DHM). Generally, by trading with other degrees of freedom, the spatial resolution is enhanced, and a large field of view (FOV) is preserved (Table 1). Resolution enhancement approaches can be classified into two categories, namely, lens-based DHM and lens-free DHM, based on whether an objective lens is used. In lens-based DHM, oblique illumination, structured illumination, and speckle illumination were used to enhance the spatial resolution of DHM. In sample-distant lens-free DHM, self-extrapolation of holograms can enhance the physical-aperture-limited spatial resolution. Furthermore, the resolution can be further enhanced by synthesizing a larger hologram by scanning the sample, camera, illumination, or inserting a diffraction grating between the sample and the camera. With a lens-free on-chip DHM, resolution enhancement can be obtained by pixel super-resolution and a synthetic aperture by shifting the illumination beam. Recently, deep learning has also been used to enhance the resolution in DHM. Being trained with plenty experimental datasets obtained under well-controlled imaging conditions, deep neural networks enable the enhancement of the spatial resolution or the SBP of DHM in a rapid, non-iterative manner. It is worth pointing out that the resolution enhancement approaches in DHM can surpass the resolution limited by the geometry (NA) of the imaging system in terms of 0.82λ/NA. However, they cannot surpass the physical diffraction limit λ(2NA)152 in far-field imaging.
Technique/Methods Features/Capabilities References DHM using an
imaging lensOblique illumination
Structured illumination
Speckle illumination● Complex configuration due to the usage of an objective, suffers from objective-related aberration
● Achievable resolution: $ \sigma =\frac{{\kappa }_{1}\lambda }{N{A}_{imag}+N{A}_{illum}} $
● Resolution enhancement factor of 2~5, depending on NAillum/NAimag.
● FOV is limited by the objective design: 1x1 mm2 under a 10× objective, etc.49, 77, 96 DHM without using an imaging lens Self-extrapolation of holograms ● No extra measurement is needed
● Achievable resolution is λz/(NΔS) instead of λz/(N0ΔS), when the hologram is effectively extrapolated from N0ΔS to NΔS.104, 106-108 Hologram expansion by shifting the CCD or the sample ● Achievable resolution: δ=λz/Lhologram
● Effective NA up to 0.3, and FOV: up to 20×16 mm2110, 112, 113 Pixel super-resolution for
on-chip DHM● Subpixel-shifts (e.g.,6×6) of hologram yields an NA of 0.9
● Oblique illumination further enhances NA to 1.4 and improves the SNR.
● FOV up to 20 mm2116, 118, 125, 128, 129124 AI algorithm based techniques Deep-learning ● Relies on large-scale data sets, time-consuming.
● Reconstruction can be wrong if the training data is inadequate.
● Resolution is diffraction limited.144,148 Table 1. Overview of Different Resolution enhancement techniques for DHM
In the past decade, intensive efforts have been made to achieve coherent imaging resolution beyond the diffraction limit. There are two coherent imaging approaches that can achieve super-resolution capability. The first is synthetic-aperture DHM using evanescent waves, which can exceed the diffraction limit in the near-field region. The second is super-oscillation illumination or super-oscillatory lens-based optical microscopy153. We envisage that there will be an increasing number of investigations concerning the physics of DHM resolution enhancement, and these investigations will widen the applications of DHM in different fields.
-
The authors acknowledge the support from the National Key Research and Development Program of China (2021YFF0700300), the National Natural Science Foundation of China (NSFC 62075177, 62175112), the Natural Science Foundation of Shaanxi Province (2020JM-193 and 2020JQ-324), and the Fundamental Research Funds for the Central Universities (XJS210503, XJS210504, JC2112, and JB210513).
Resolution enhancement of digital holographic microscopy via synthetic aperture: a review
- Light: Advanced Manufacturing 3, Article number: (2022)
- Received: 03 September 2021
- Revised: 18 January 2022
- Accepted: 19 January 2022 Published online: 27 January 2022
doi: https://doi.org/10.37188/lam.2022.006
Abstract: Digital holographic microscopy (DHM), which combines digital holography with optical microscopy, is a wide field, minimally invasive quantitative phase microscopy (QPM) approach for measuring the 3D shape or the inner structure of transparent and translucent samples. However, limited by diffraction, the spatial resolution of conventional DHM is relatively low and incompatible with a wide field of view (FOV) owing to the spatial bandwidth product (SBP) limit of the imaging systems. During the past decades, many efforts have been made to enhance the spatial resolution of DHM while preserving a large FOV by trading with unused degrees of freedom. Illumination modulation techniques, such as oblique illumination, structured illumination, and speckle illumination, can enhance the resolution by adding more high-frequency information to the recording system. Resolution enhancement is also achieved by extrapolation of a hologram or by synthesizing a larger hologram by scanning the sample, the camera, or inserting a diffraction grating between the sample and the camera. For on-chip DHM, spatial resolution is achieved using pixel super-resolution techniques. In this paper, we review various resolution enhancement approaches in DHM and discuss the advantages and disadvantages of these approaches. It is our hope that this review will contribute to advancements in DHM and its practical applications in many fields.
Research Summary
Resolution enhancement of digital holographic microscopy: a review
Digital holographic microscopy (DHM) is a wide-field, minimally invasive quantitative phase microscopy approach for measuring the 3D shape or the inner structure of transparent and translucent samples. However, limited by diffraction, the spatial resolution of conventional DHM is relatively low, and therefore, tinny structures of samples can be not seen under conventional DHM. During the past decades, many efforts have been made to enhance the spatial resolution of DHM while preserving a large field of view (FOV). Peng Gao from Xidian University and Cao-jin Yuan from Nanjing Normal University present a comprehensive review of resolution enhancement approaches for DHM, which encompass illumination engineering, hologram extrapolation or synthesis, pixel super-resolution, and artificial intelligence (AI) approaches. They also discussed and summarized the advantages and disadvantages of these resolution enhancement approaches.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article′s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article′s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

























 DownLoad:
DownLoad: