Metasurfaces designed by a bidirectional deep neural network and iterative algorithm for generating quantitative field distributions

Metasurfaces, which consist of predesigned meta-atoms with different shapes or in-plane orientations, have demonstrated unprecedented capabilities in the local manipulation of the amplitude, phase, and polarisation of electromagnetic (EM) waves^{1, 2}. Unlike traditional bulky counterparts that are often dependent on the phase accumulation of light propagation, the fundamental principle of metasurface-based devices relies on abrupt phase changes at planar meta-atom interfaces³⁻⁵. Therefore, metasurfaces provide a robust platform for designing ultracompact components, enabling tremendous advantages in device miniaturisation and system integration. In addition, owing to the ultra-flexibility of the metasurface design, metasurface-based devices possess various unusual functionalities that are extremely difficult or impossible to achieve with natural materials. Empowered by metasurfaces with a delicately designed structure and multifunctional integration properties, a plethora of applications including a beam deflector⁶⁻⁹, vortex beams¹⁰⁻²⁰, holograms²¹⁻²⁸, metalenses²⁹⁻³⁷, wave plates³⁸⁻⁴² and nonlinear photonics^{43, 44} have been demonstrated. Although metasurfaces have presented several advances in tailoring the wavefront of EM waves, the current matasurface-based devices with sophisticated functionalities have an increased structural complexity. The conventional design approach relies on iterative numerical full-wave simulations, such as the finite-difference time-domain (FDTD) method, finite-element method (FEM), and finite integration technique (FIT). Following a comparison between the calculated result and target response, structural parameters are numerically optimised to update the design. Aiming to achieve extreme performances, optimising multiple structural parameters becomes computationally costly, which regularly requires hundreds of thousands, or even millions of simulations to obtain a reasonable design.

Artificial neural networks (ANNs)⁴⁵⁻⁵², which is a data-driven approach, can be trained to assist in the design process with a high-efficiency. Owing to the unprecedented capabilities in recognition, processing, and optimisation, ANNs have gained considerable attention in several areas including computer version⁵³, image recognition⁵⁴, cloaking⁵⁵, deep mapping⁵⁶, among others. In nanophotonics, ANNs can be applied for accurately predicting the resonant spectra and inversely designing the device structures (or vice versa). Differing from the traditional design methods, ANNs enable the capability of automatically learning the hidden relationship between the neurons in different layers (the relationship between the photonic structures and corresponding optical responses) from the training data, which can assist in determining the preconceived functionality, and therefore, significantly accelerating and simplifying the design process. ANNs applied in designing photonics devices are generally divided into the following two categories: forward neural networks and inverse neural networks. For the forward neural networks, structural parameters, such as the geometric parameters of length, width, and height, are assigned as the input to predict the EM response of the device. These type of ANNs can replace the conventional EM simulations in the optimisation loop, leading to a significantly reduced design time^{57, 58}. For the inverse neural networks, the EM response is considered as the input for generating the device structure. The structural design accomplished by this type of ANN can be achieved in a fraction of second without the process of numerical optimisation^{59, 60}. Benefiting from the outstanding design and optimisation capabilities, ANNs have been applied in designing metasurfaces for various applications, such as beam deflectors⁶¹⁻⁶³, metalenses⁶⁴⁻⁶⁷, and functionality multiplexing⁶⁸. However, the current metasurface designs assisted by the ANNs are restricted to generating qualitative phenomena and field distributions, such as beam deflecting, focusing, and holography. A metasurface-based device with quantitative wavefront-modulation functionalities can enable practical applications such as imaging, detecting, and sensing; therefore, the design of metasurface-based devices (assisted by ANNs) with high-accuracy functionalities is significantly desirable.

In this study, we conceptually propose a bidirectional deep neural network combined with an iterative algorithm to accurately design metasurface-based devices that can manipulate incident terahertz (THz) waves with quantitative field distributions. A bidirectional deep neural network called the tandem neural network⁶⁹⁻⁷³, which consists of an inverse design network and a forward-modeling network, is designed to efficiently predict structural parameters and avoid the non-uniqueness issues encountered in the inverse process. In addition, an iterative algorithm is introduced and assisted with the tandem neural network to further optimise the metasurface design, resulting in quantitative field distributions. As proof-of-principle examples, metalenses generating two focal points with identical/orthogonal polarisation states and accurate intensity ratios are predicted by the network architecture constructed in this study. The customised electric-field intensity distributions and intensity ratios between these two focal points are numerically simulated and experimentally demonstrated based on designed metasurface devices. Note, the approach of combining the tandem neural network and iterative algorithm can accurately design metasurface-based devices that can manipulate the incident THz waves with quantitative field distributions, which are different from the prediction of the transmission spectra of the designed structures (or vice versa) and qualitative field distributions in the previous studies⁶⁹⁻⁷³. The unique design strategy and experimental demonstration in this study will promote machine learning in further designing ultracompact devices with high-accuracy and quantitative functionalities.

Fig. 1a presents schematics of the designed multi-foci metalenses that can generate polarisation-dependent multiple focal points with a precise intensity ratio. Under the illumination of the x-polarised THz waves (top schematic in Fig. 1a), the metalens can focus the incident THz waves onto the two x-polarised focal points with a predesigned intensity ratio. For the incidence of THz waves with polarisation along the diagonal direction (bottom schematic in Fig. 1a), the other designed metalens can generate two orthogonally-polarised focal points, that is, one x-polarised focal point and one y-polarised focal point, with an accurate intensity ratio. Fig. 1b, c present the optical images of the fabricated samples where each sample consists of 100 × 100 meta-atoms with different sizes. The meta-atoms in each metalens are delicately designed by our proposed network architecture to accurately modulate the incident THz waves to generate identically (Fig. 1b) or orthogonally (Fig. 1c) polarised focal points with customisable intensity ratios.

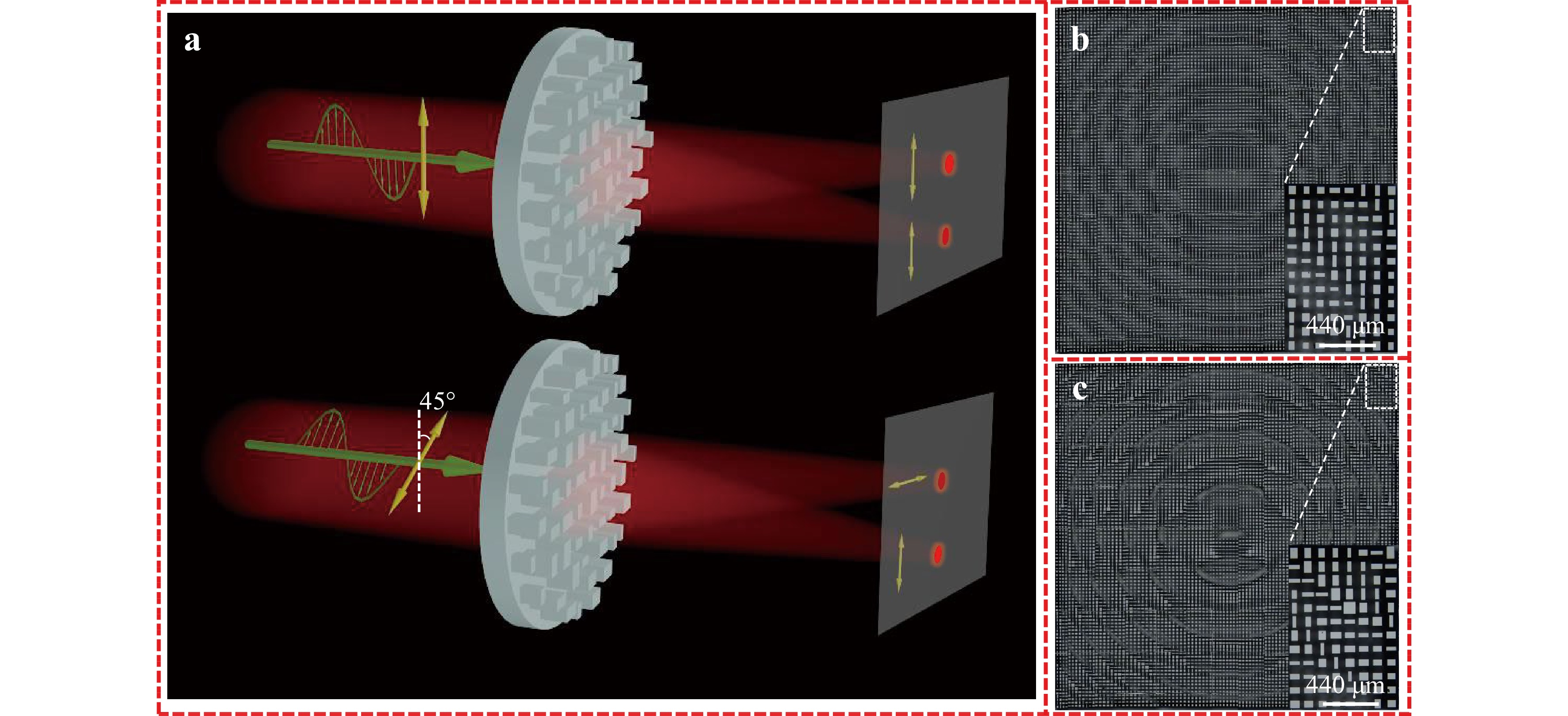
Fig. 1  Schematics and optical images of the polarisation-dependent multi-foci metalenses with a customisable intensity ratio. a Schematics of the metalenses for generating identically (top image) or orthogonally (bottom image) polarised focal points with a customisable intensity ratio. The optical images of metalenses for generating: identically b or orthogonally c polarised focal points with a customisable intensity ratio.

To delicately design the metasurface device with quantitative field distributions, a network architecture consisting of a tandem neural network combined with an iterative algorithm is proposed to predict and optimise the required structure, as shown in Fig. 2a. The tandem neural network shown in Fig. 2b contains the following two parts: an inverse design network and forward-modeling network. The inverse design network is trained to construct a connection between the characteristics (amplitudes and phases) of the focal points and structural parameters (width and length) of meta-atoms. When the four parameters (L₁(1), L₁(2), L₁(3), L₁(4)) are considered as the input, which are two real and two imaginary parts corresponding to the amplitudes and phases of the two focal points, the output is indicated by O₁ and O₂, which are the length and width of the silicon meta-atom. A single inverse design network for predicting the structural parameters will inevitably suffer from a severe non-uniqueness issue that is defined as having several solutions^{62, 64}, that is, several different geometric parameters of the device corresponding to a similar EM response; thus, the neural network would hardly converge. To effectively overcome this issue, a pretrained forward neural network (PFNN) (right part in Fig. 2b) is introduced and connected to the inverse neural network. The PFNN is already independently trained and obtains the structural parameters (generated from the inverse neural network) as the input, and subsequently outputs the amplitudes and phases illustrated by the four parameters of L₂(1), L₂(2), L₂(3), and L₂(4). The weights in the PFNN are fixed, while the weights in such a tandem neural network are trained to further reduce the loss function that is defined as the least-square errors between the output (L₂(1), L₂(2), L₂(3), L₂(4)) and input (L₁(1), L₁(2), L₁(3), L₁(4)) parameters, which is expressed as $ Loss = {1}/{N}\displaystyle\sum\limits_{i = 1}^N {{{({L_1}(i) - {L_2}(i))}^2}} $ (i = 1, 2, 3, 4). Although the aforementioned bidirectional deep neural network enables the functionality of predicting highly accurate metasurface devices to generate a variety of qualitative field distributions, stricter metasurface designs with quantitative field distributions should be designed by further introducing an iterative algorithm (Fig. 2c, d) to assist with the structural optimisation. After numerical simulations based on the structural parameters generated from the tandem neural network, the intensity ratio (η) between the left (I_L-side) and right (I_R-side) focal points is obtained. Subsequently, the iterative algorithm shown in Fig. 2c (or Fig. 2d) is designed to further optimise the ratio of the amplitudes between the left (A/A_x) and right (B/B_y) focal points with identically/orthogonally linearly-polarised (LP) states. When the intensity ratio between these two focal points is optimised and numerically simulated in the region $ {\eta _0} - \Delta \eta < \eta < {\eta _0} + \Delta \eta $ ($ {\eta _0} $ is the target intensity ratio, $ \Delta \eta = 0.005 $ is the tolerance level, and ξ = 0.05 (it is a compensation coefficient, or defined as an iterative coefficient, that can adjust the parameters “B”, “A_x”, or “B_y” to satisfy the condition of “$ {\eta _0} - \Delta \eta \leqslant \eta \leqslant {\eta _0} + \Delta \eta $”)), the optimisation routine is finished, and the final structural parameters are generated from the tandem neural network. Further details regarding the designed method based on our proposed algorithm can be found in the supplementary materials of Section 1.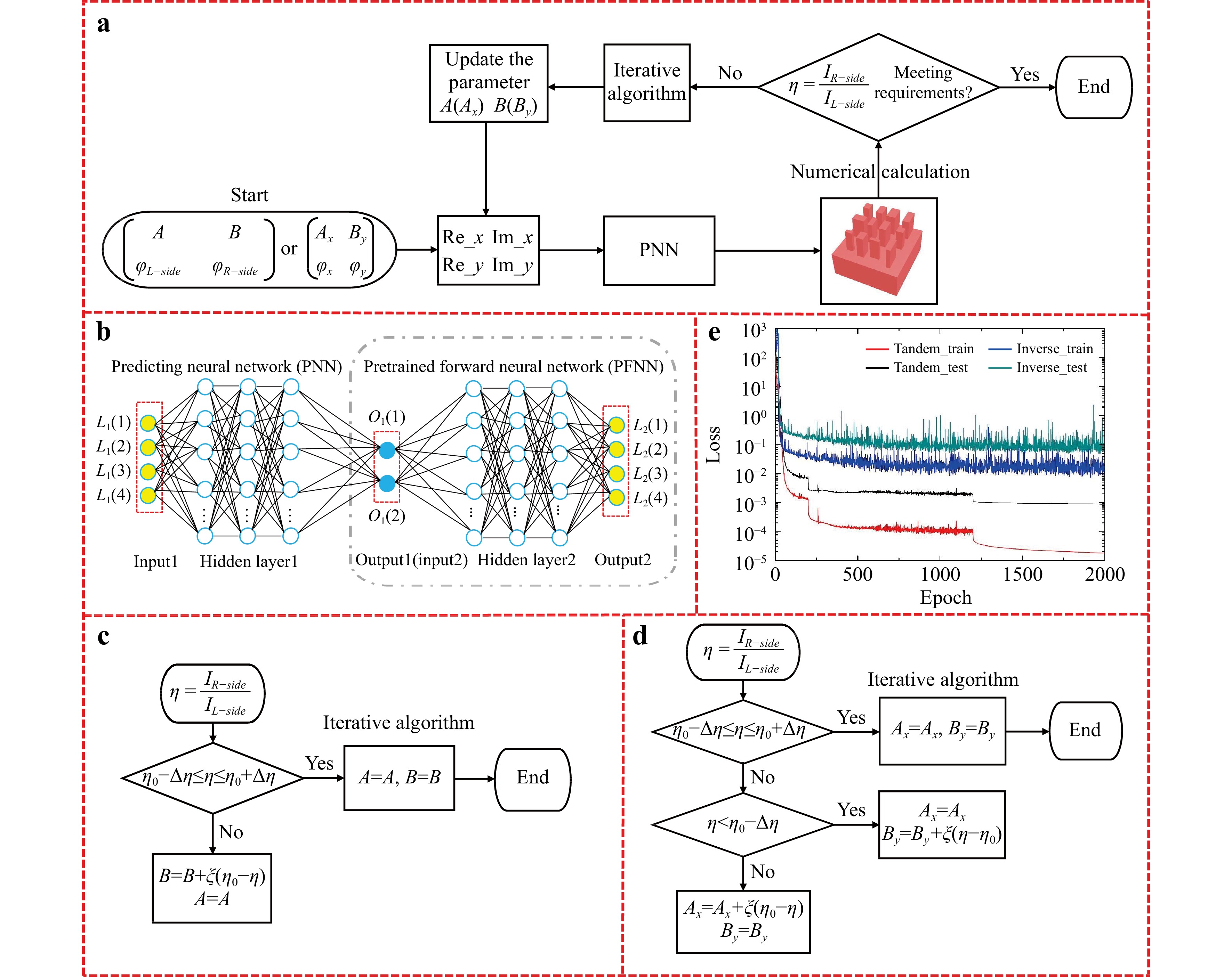

Fig. 2  Flow chart of the network architecture for designing metasurface devices with quantitative field distributions. a Sketch of a metasurface design based on the tandem neural network and iterative algorithm. b Tandem neural network for predicting the structural parameters of metasurface devices. c, d Detailed flow charts of the iterative algorithm to further assist in structural optimisation. e Loss function of the training and test sets for the direct inverse network (cyan and blue curves) and tandem network (black and red curves).

In this study, silicon meta-atoms with a variable width (W) and length (L), but a fixed height of 500 µm (sitting on the silicon substrate with a thickness of 500 µm) are predicted and optimised to achieve the predesigned functionalities. To establish such a tandem neural network, various training instances were simulated in advance to train both the inverse design network and forward-modeling network. The period of the unit cell was 110 µm, and the working frequency of the designed meta-atoms was 0.7 THz. The width of the meta-atoms ranged from 30 to 100 µm, while the parameter sweep of length was also changed from 30 to 100 µm with a scanning step of 1 µm. The finite difference time domain method was applied to calculate 5041 samples, where 80% of instances were used as the training set and the remaining 20% were assigned as the test set. For the inverse design network, four units (amplitude and phase of the meta-atoms) were obtained as the input and directly output two units (width and length of the met-atoms). It possessed three fully connected hidden layers with 200, 500, and 100 neurons, respectively. The forward-modeling network obtained two units (the output of the inverse design network) as the input and predicted the EM response (amplitude and phase) and also has three hidden layers with 100, 500, and 100 neurons. By combining the inverse network with the PFNN, the tandem neural network with the loss rapidly decreased to ~10⁻⁵, while a single inverse network had a loss of ~10⁻² after 1500 iterations (see Fig. 2e). The required metalens with 10000 (100 × 100) meta-atoms can be predicted in 0.67 s by our trained tandem neural network.

To verify the protoptype, we first design and experimentally demonstrate a metalens that can be predicted by our proposed network architecture to generate two focal points with identical polarisation states and a customisable intensity ratio between them. To generate two LP focal points, the metalens with the required phase profile can be expressed as follows: $ {\varphi _{L {\text -} side}} = k({f_{L {\text -} side}} - \sqrt {{f_{L {\text -} side}}^2 + {{(x - {x_{L {\text -} side}})}^2} + {{(y - {y_{L{\text -} side}})}^2}} ) $ and $ {\varphi _{R{\text -} side}} = k({f_{R{\text -} side}} - \sqrt {{f_{R{\text -} side}}^2 + {{(x - {x_{R{\text -} side}})}^2} + {{(y - {y_{R {\text -} side}})}^2}} ) $. $ {\varphi _{L {\text -} side}} $ and $ {\varphi _{R{\text -}side} }$ are two phase profiles introduced in the metalens to simultaneously focus the incident x-polarised THz waves into two focal points located at the two positions of ($ {x_{L{\text -} side}} $, $ {y_{L{\text -} side}} $, $ {f_{L{\text -} side}} $) and ($ {x_{R {\text -} side}} $, $ {y_{R{\text -} side}} $, $ {f_{R{\text -} side}} $). A and B are the amplitudes of these two focal points. The corresponding parameters for focusing are theoretically designed as follows: $ {x_{L {\text -} side}} = - {x_{R {\text -} side}} = - 2\begin{array}{*{20}{c}} {mm} \end{array} $, $ {y_{L {\text -} side}} = {y_{R {\text -} side}} = 0 $, and $ {f_{L{\text -} side}} = {f_{R {\text -} side}} = 6\begin{array}{*{20}{c}} {mm} \end{array} $. The initial values for these two parameters (A and B) are assigned as 1 (A=B=1). Subsequently, the four parameters as the input of the proposed network architecture are ${L_1}(1) = $ $ real(A\exp (i{\varphi _{L{\text -} side}})) $, $ {L_1}(2) = imaginary(A\exp (i{\varphi _{L{\text -} side}})) $, $ {L_1}(3) = real(B\exp (i{\varphi _{R{\text -} side}})) $, and ${L_1}(4) = $ $ imaginary(B\exp (i{\varphi _{R {\text -} side}})) $. The tandem neural network is pretrained to initially predict the structural parameters, while the iteration algorithm is designed to further optimise the ratio between A and B to obtain the accurate device geometry that enables a customisable intensity ratio between two focal points. Fig. 3a1 presents the calculated electric-field intensity distribution of the metalens designed by our network architecture. Under the illumination of the x-polarised THz waves, two focal points with identical polarisation states are observed and symmetrically distributed at (−2 mm, 0, 5.7 mm) and (2 mm, 0, 5.7 mm), respectively. The target intensity ratio (at the focal plane) between these two focal points is 1:1, and the predicted metalens with the calculated intensity ratio (at the focal plane of z = 5.7 mm) is also I_L-side : I_R-side = 1 : 1 (see Fig. 3c1), which is accurately matched with the target value. According to the predicted structural parameters, the corresponding sample is fabricated with traditional photolithography. Fig. 3b1 presents the measured electric-field intensity of the designed metalens based on our near-field scanning THz time-domain spectrum microscopy system. For the incidence of the x-polarised THz waves, two x-polarised focal points are generated. The measured intensity ratio of the two focal points at the focal plane (z = 5.7 mm) is I_L-side : I_R-side = 1 : 0.992, as shown in Fig. 3d1. The measured result sufficiently matches with the numerical simulation except for a slight discrepancy, which can be attributed to the error of the imperfect sample. To further verify the versatility and high performance of our network architecture, metalenses with an unequal intensity ratio between two focal points are designed and demonstrated. Fig. 3a2, b2 present the calculated and measured electric-field distributions following the designed metalens, which can generate two focal points with different intensities. The calculated intensity ratio in this case is I_L-side : I_R-side = 1 : 0.799, which sufficiently agrees with the target value of I_L-side : I_R-side = 1 : 0.8, while the measured intensity ratio is I_L-side : I_R-side = 1 : 0.74. In addition, the target intensity ratio between the two focal points of I_L-side : I_R-side = 1 : 0.6 is also numerically and experimentally demonstrated in Fig. 3a3−d3, where the intensity ratios are I_L-side : I_R-side = 1 : 0.599 (Fig. 3b3) in the simulation and I_L-side : I_R-side = 1 : 0.63 (Fig. 3d3) in the experiment. The optical and SEM (scanning electron microscope) images of the samples are shown in the supplementary materials of Section 2 of Figs. S1 and S2. The corresponding electric-field intensity distributions and predicted amplitudes and phases (for the aforementioned three cases) in the x-y plane are provided in the supplementary materials of Section 3 of Figs. S3 and S4. The ratios between parameters A and B and the corresponding efficiencies (in the experiment) are presented in supplementary of Tables 1 and 3, respectively.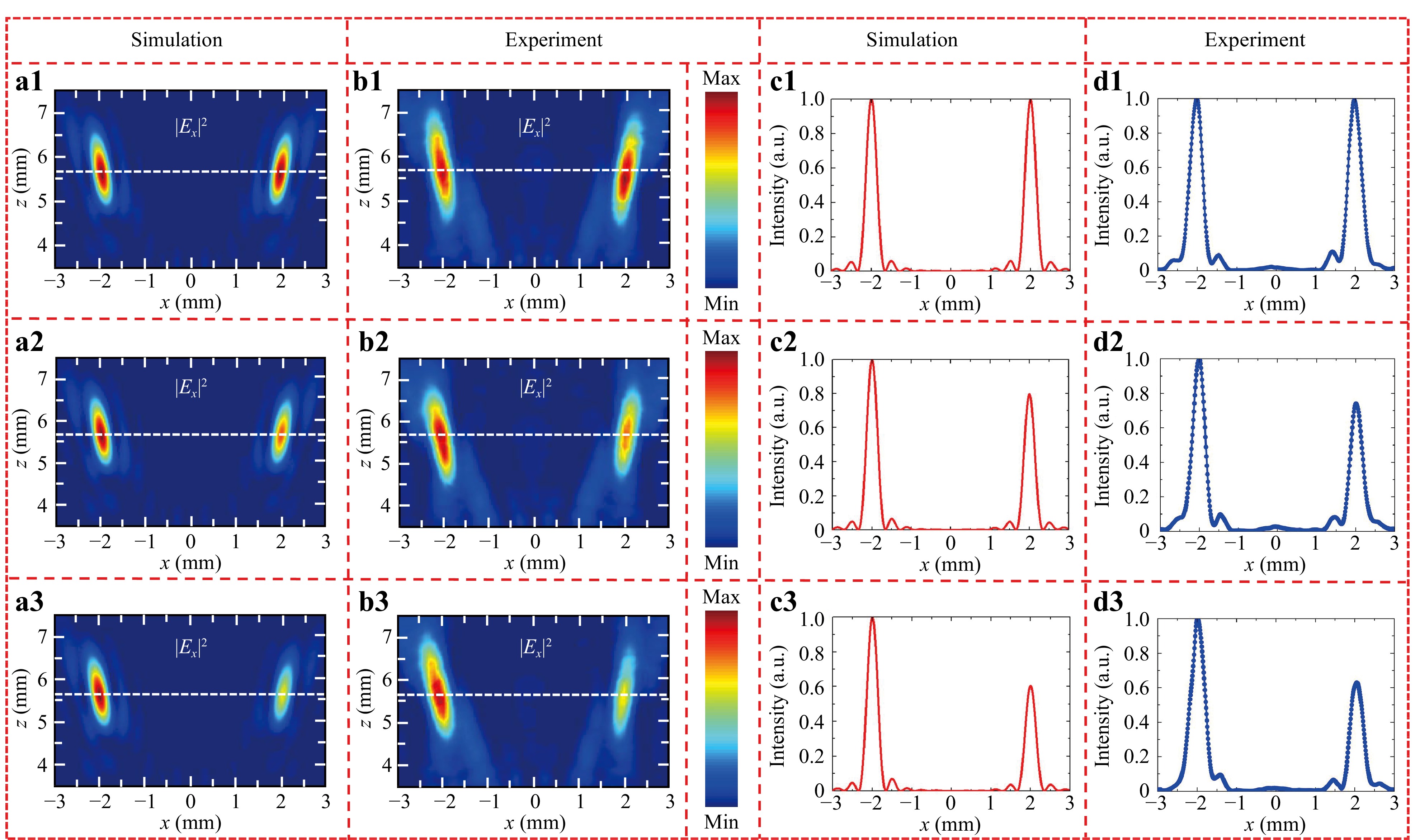

Fig. 3  The calculated and measured electric-field intensity distributions based on the metalenses that can generate two focal points with identical polarisation states and is designed by the proposed network architecture. The calculated a1, c1 and measured b1, d1 electric-intensity distributions at the x-z plane (and z = 5.7 mm) for the target intensity ratio between these two focal points is I_L-side : I_R-side = 1 : 1. The calculated a2, c2 and measured b2, d2 electric-intensity distributions at the x-z plane (and z = 5.7 mm) for the target intensity ratio between these two focal points is I_L-side : I_R-side = 1 : 0.8. The calculated a3, c3 and measured b3, d3 electric-intensity distributions at the x-z plane (and z = 5.7 mm) for the target intensity ratio between these two focal points is I_L-side : I_R-side = 1 : 0.6.

In addition to the modulation of focal points with identical polarisation states and a predesigned intensity ratio, the proposed network architecture can also be extended to design metalens that can generate two focal points with orthogonal polarisation states and a customisable intensity ratio; the polarisation of an incident LP THz wave is along the diagonal direction. The phase requirement (for the metalens) to simultaneously focus the x- and y-polarised THz waves is governed by $ \varphi = \arg ({B_y}\exp (i{\varphi _{L{\text -} side}}) + {A_x}\exp (i{\varphi _{R{\text -} side}})) $, where $ {\varphi _{L{\text -} side}} = k({f_{L {\text -} side}} - \sqrt {{f_{L {\text -} side}}^2 + {{(x - {x_{L {\text -} side}})}^2} + {{(y - {y_{L{\text -} side}})}^2}} ) $ and $ {\varphi _{R {\text -} side}} = k({f_{R{\text -}side}} - \sqrt {{f_{R {\text -} side}}^2 + {{(x - {x_{R {\text -} side}})}^2} + {{(y - {y_{R {\text -} side}})}^2}} ) $. Here, $ {\varphi _{L {\text -} side}} $($ {\varphi _{R {\text -} side}} $) is the phase profile embedded in the metalens to focus the incident y-polarised (x-polarised) THz waves onto y-polarised (x-polarised) focal points. A_x and B_y are the corresponding amplitudes for the x-polarised and y-polarised focal points, respectively. The corresponding parameters for the focal points are selected as follows: $ {x_{L {\text -}side}} = - {x_{R {\text -} side}} = - 1\begin{array}{*{20}{c}} {mm} \end{array} $, $ {y_{L{\text -} side}} = {y_{R{\text -} side}} = 0 $, and $ {f_{L{\text -} side}} = {f_{R {\text -} side}} = 6\begin{array}{*{20}{c}} {mm} \end{array} $. As shown by Fig. 4a1, a2 for the incident THz beams with polarisation along the x- and y-directions, two focal points consisting one x-polarised focal point (in the right side) and one y-polarised focal point (in the left side) are observed. The calculated intensity ratio between these two focal points (see Fig. 4c1) is I_L-side : I_R-side = 0.993 : 1 (the target value is I_L-side : I_R-side = 1 : 1). The measured electric-field intensity distributions are shown in Fig. 4b1, b2, and the corresponding intensity ratio between these two focal points is I_L-side : I_R-side = 1 : 0.98 (see Fig. 4c2). For the case with target intensity ratio of I_L-side : I_R-side = 0.8 : 1 (between the y- and x-polarised focal points), the simulated and measured electric-field intensity distributions are shown in Fig. 4a3, a4 and Fig. 4b3, b4. The calculated and measured intensity ratios in this case are I_L-side : I_R-side = 0.8 : 1, and I_L-side : I_R-side = 0.78 : 1, respectively (see Fig. 4c3, c4). In addition, for the case with the target intensity ratio of I_L-side : I_R-side = 0.6 : 1, both the numerical and measured results shown in Fig. 4a5, a6 and Fig. 4b5, b6 also demonstrate two focal points with orthogonal polarisation states and different intensity distributions. The simulated and measured intensity ratios in the focal plane are I_L-side : I_R-side = 0.6 : 1, and I_L-side : I_R-side = 0.55 : 1 (Fig. 4c5, c6), respectively. The optical and SEM images of the fabricated samples are shown in the supplementary materials of Section 2 of Figs. S1 and S2. The corresponding electric-field intensity distributions and predicted amplitudes and phases (for the three aforementioned cases) in the x-y plane are provided in the supplementary materials of Section 4 of Figs. S5 and S6. The ratios between parameters A_x and B_y and the corresponding efficiencies (in experiment) are presented in supplementary of Tables 2 and 4, respectively.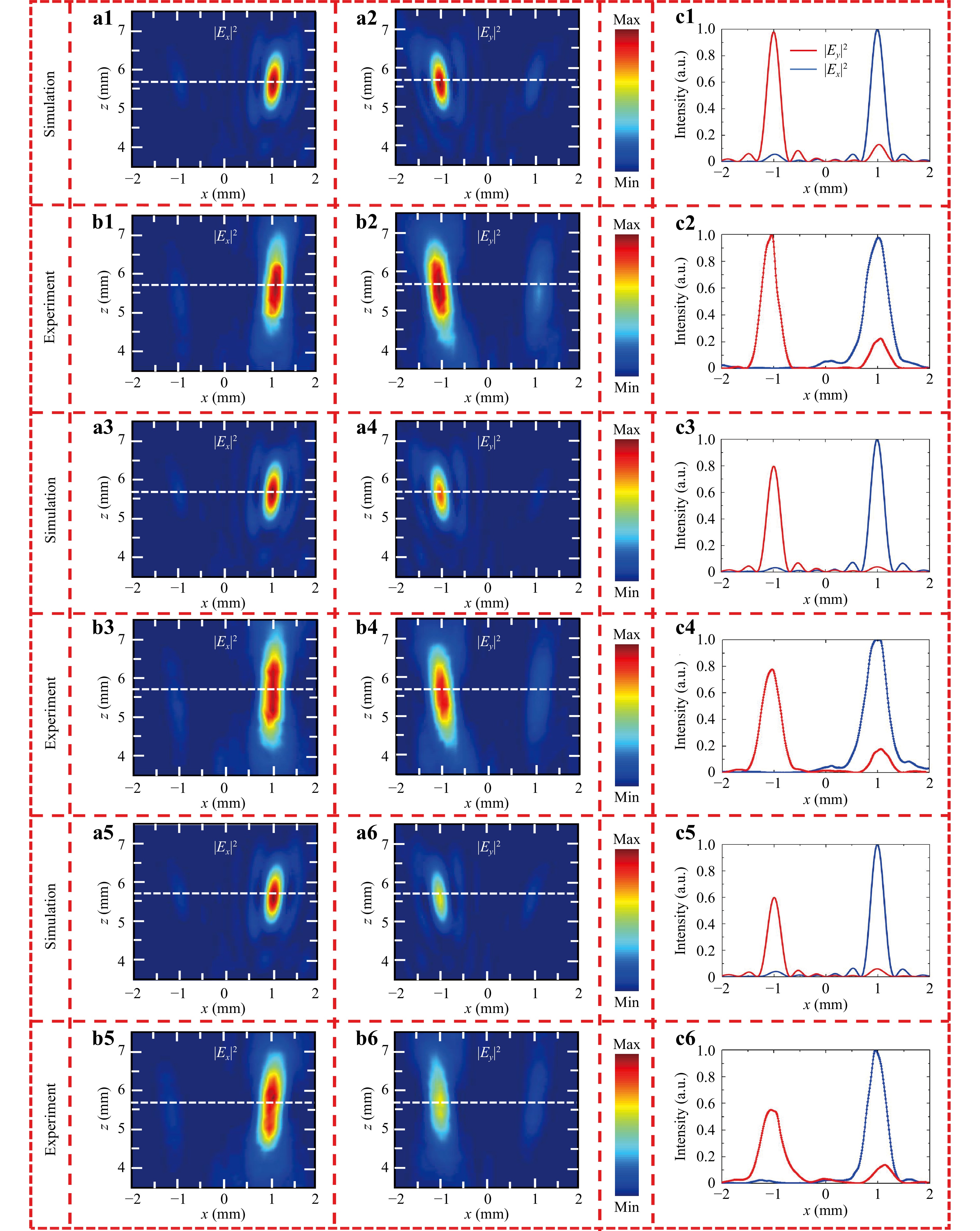

Fig. 4  The calculated and measured electric-field intensity distributions based on the metalenses that can generate two focal points with orthogonal polarisation states and is designed by the proposed network architecture. The calculated a1, a2, c1 and measured b1, b2, c2 electric-intensity distributions at the x-z plane (and z = 5.7 mm) for the target intensity ratio between these two focal points is I_L-side : I_R-side = 1 : 1. The calculated a3, a4, c3 and measured b3, b4, c4 electric-intensity distributions at the x-z plane (and z = 5.7 mm) for the target intensity ratio between these two focal points is I_L-side : I_R-side = 0.8 : 1. The calculated a5, a6, c5 and measured b5, b6, c6 electric-intensity distributions at the x-z plane (and z = 5.7 mm) for the target intensity ratio between these two focal points is I_L-side : I_R-side = 0.6 : 1.

In addition to our proposed network architecture allowing the design of metalens having quantitative field distributions, it also enables the ability to design a metasurface device to harness the THz waves with qualitative field distributions without the assistant of an iterative algorithm. As a proof-of-principle example, a vortex generator that can generate position- and polarisation-dependent converged vortices is designed by the tandem neural network. The corresponding phase profile encoded in the device is $ \varphi = \arg ({B_y}\exp (i{\varphi _{L {\text -} side}}) + {A_x}\exp (i{\varphi _{R{\text -} side}})) $, where $ {\varphi _{L{\text -}side}} = k({f_{L {\text -} side}} - $ $\sqrt {{f_{L {\text -} side}}^2 + {{(x - {x_{L{\text -} side}})}^2} + {{(y - {y_{L {\text -} side}})}^2}} ) + {l_1}\theta $ and $ {\varphi _{R {\text -} side}} = k({f_{R {\text -} side}} - \sqrt {{f_{R {\text -} side}}^2 + {{(x - {x_{R {\text -} side}})}^2} + {{(y - {y_{R {\text -} side}})}^2}} ) + {l_2}\theta $. $ {\varphi _{L {\text -} side}} $ and $ {\varphi _{R {\text -} side}} $ are the phase profiles for converting the incident LP THz waves into one y-polarised and one x-polarised converged vortex in different positions. The polarisation of an incident LP THz wave occurs diagonally. The theoretically designed parameters for such a vortex generator are $ {l_1} = {l_2} = - 1 $, $ {x_{L {\text -} side}} = - {x_{R {\text -} side}} = - 1\begin{array}{*{20}{c}} {mm} \end{array} $, $ {y_{L {\text -} side}} = {y_{R {\text -} side}} = 0 $, $ {f_{L {\text -} side}} = {f_{R {\text -}side}} = 6\begin{array}{*{20}{c}} {mm} \end{array} $, and $ {A_x} = {B_y} = 1 $. The structural parameters are predicted by the tandem neural network according to the phase profile (φ); subsequently, the geometry of the device is created for the numerical simulation. Fig. 5a1, a2 present the electric-field intensity distributions of the designed vortex generators under the illumination of x- and y-polarised THz waves. For the incidence of the x-polarised THz waves, a converged vortex with polarisation along the x-axis is observed at 1, 0, and 5.7 mm, whereas the other converged vortex with polarisation along the y-axis is observed under the illumination of the y-polarised THz waves and located at –1 mm, 0, and 5.7 mm. The corresponding phase distributions are shown in Fig. 5b1, b2; there is only one phase jump from –π to π for each converged vortex, which demonstrates that the topological charge of each converged vortex is –1. The experimental demonstration of such a designed vortex generator is shown in Fig. 5a3−b4. The x-polarised (y-polarised) converged vortex is experimentally observed when the sample is under the illumination of the x-polarised (y-polarised) THz waves (Fig. 5a3, a4). The corresponding phase distributions shown in Fig. 5b3, b4 also demonstrate that the topological charge of each converged vortex in the experiment is -1. The optical and SEM images of the fabricated samples are shown in the supplementary materials of Section 2 of Figs. S1 and S2. The corresponding electric-field intensity distributions in the x-z plane, and the predicted amplitudes and phases for the vortex generator are provided in the supplementary materials of Section 5 of Figs. S7 and S8. In addition, the simulated vortices with various topological charges and orthogonal polarisation states are presented in the supplementary materials of Section 6 of Figs. S9 and S10.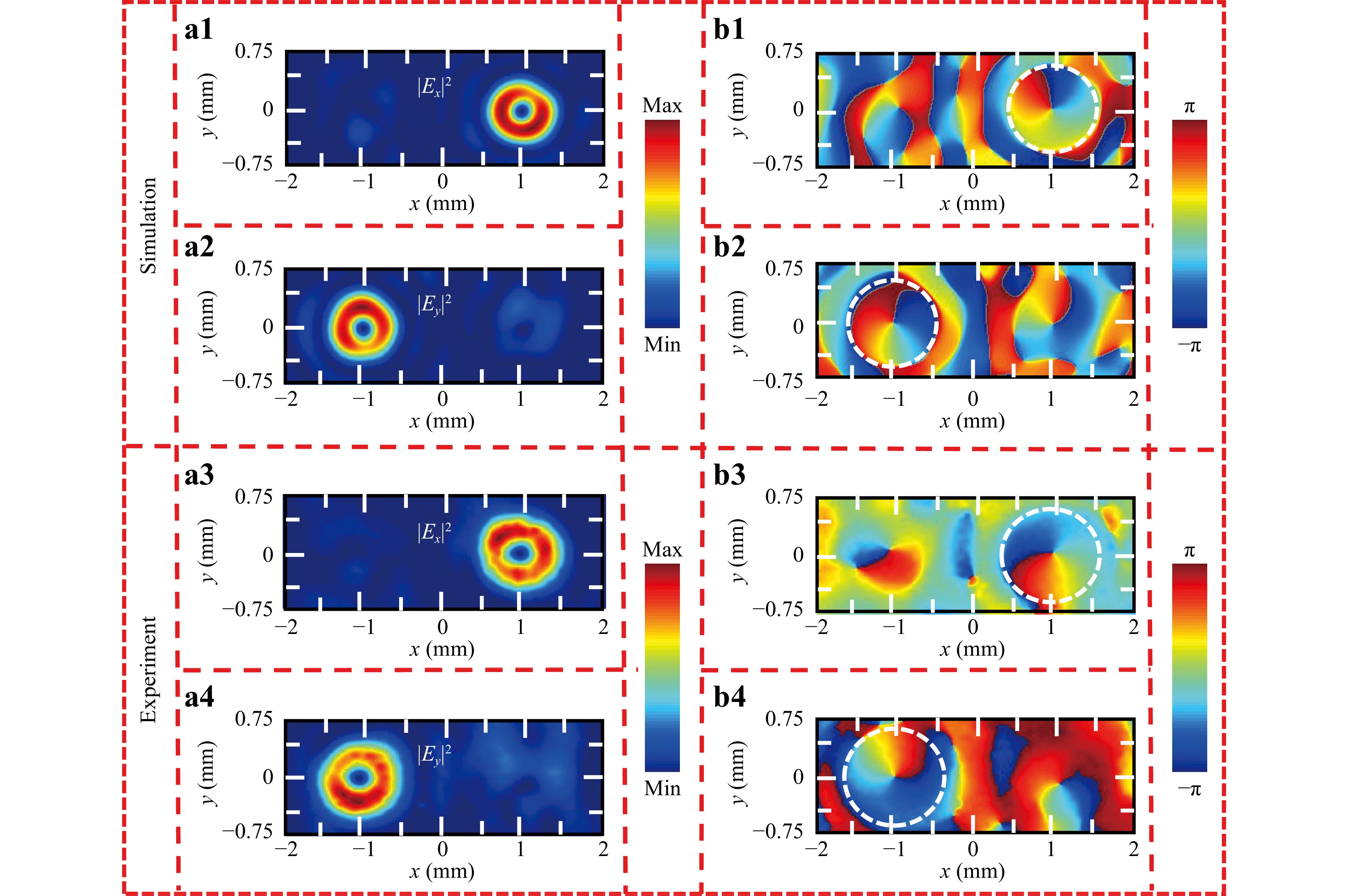

Fig. 5  The calculated and measured electric-field intensity and phase distributions based on the metasurface devices that can generate two converged vortices with orthogonal polarisation states and are designed by the tandem neural network. The calculated electric-field a1, a2 and phase b₁, b₂ distributions at the focal plane z = 5.6 mm. The measured electric-field a3, a4 and phase b3, b4 distributions at the focal plane z = 5.6 mm.

A critical advantage of our proposed algorithm is the combination of the tandem neural network and iterative algorithm to automatically and intelligently optimise the ratio between A (A_x) and B (B_y), thus globally optimising all the amplitudes and phases that can be applied to predict the structural parameters for designing appropriate metasurfaces. The detailed advantages of our proposed algorithm are as follows: (1) In the traditionally forward design, the ratio between A(A_x) and B(B_y) needs to be manually altered, which is time-consuming and unintelligent. However, the proposed iterative algorithm can automatically optimise the ratio between A(A_x) and B(B_y), and subsequently input the ratio into the tandem neural network to predict the structural parameters. The automatic optimisation of the ratio between A(A_x) and B(B_y) based on the iterative algorithm is faster and more intelligent than that of the manual method. (2) Designing a meta-atom with a significantly small transmission amplitude is highly complex, which is required in a traditionally forward design. For example, it cannot obtain a meta-atom with a transmission amplitude-requirement of zero. Namely, the required amplitudes and phase are fixed for each meta-atom in the traditionally forward design; therefore, the meta-atoms with a transmission amplitude, or amplitude and phase, cannot be obtained with certain inexistent values, that is, near zero. In contrast, the tandem neural network is not subjected to the amplitudes and phase requirements in the traditionally forward design. The tandem neural network enables the functionality for automatically and globally optimising all the amplitudes and phases to avoid sudden changes in the amplitude requirement (or non-selectable meta-atoms simultaneously matching the target amplitude and phase requirements in the traditionally forward design). As shown in Fig. S4 (see the supplementary materials of Section 3), when obtaining the two x-polarised focal points with an intensity ratio of 1 : 1 (based on the tandem neural network), there is a slight fluctuation in the transmission amplitudes for each meta-atom, while the phase is varied in [–π, π]. Therefore, it is easy to predict the structural parameters for designing metasurfces with quantitative field distributions based on our proposed tandem neural network combined with the iterative algorithm.

Beam splitters, which are indispensable tools, are widely used in various optical systems. For a utility THz system, it not only is determined by the high-efficiency source and detectors, but also depends on high-quality functional-devices. The pursuit of flexible and ultra-compact THz beam splitters is desirable for (THz) system integration and device miniaturisation⁷⁴. Therefore, seeking effective THz beam splitters based on metasurfaces is a popular topic owing to the lack of natural materials with the desired properties⁷⁵. Our designed metalenses predicted by a bidirectional deep neural network and iterative algorithm enable splitting the incident THz waves into two or more focal points with arbitrary energy ratios, which can be extended to design flexible and ultra-compact THz beam splitters that can split the incident THz waves into multiple beams with accurate energy ratios, leading to significant applications in coherent THz measurement systems, such as THz splitters with arbitrary energy ratios for controlling the two-beam interference⁷⁶. Such an approach not only enables the split of the incident THz waves into multiple beams with identical polarisation states, but also splits the incident THz waves into multiple beams with orthogonal polarisation states. Furthermore, our proposed method for designing meta-devices can be extended to design other ultra-compact THz components, such as THz filters, couplers, modulators, and switches.

In conclusion, we proposed a network architecture that consists of a tandem neural network and an iterative algorithm to accurately predict metasurface-based devices to manipulate THz waves with customisable/quantitative intensity distributions. The tandem neural network composed of an inverse design network, and a forward-modeling network was trained to predict the device geometry with a high-efficiency and to avoid non-uniqueness issues; meanwhile, an iterative algorithm was introduced and combined with the tandem neural network to further optimise the structural parameters of the devices, generating the quantitative electric-field distributions. Various examples such as the metalens for generating two focal points with identical/ orthogonal polarisation states and accurate intensity ratios and vortex generators for generating position- and polarisation-dependent converged vortices were numerically and experimentally demonstrated. The unique approach for predicting the metasurface devices with quantitative field distributions will introduce the design of ultracompact devices with high-accuracy functionalities.

Sample fabrication The 1000 μm intrinsic silicon wafers (<100>, Ω > 5000 ohm) were prepared for the fabrication of metasurface devices with quantitative field distributions. The silicon wafers were cleaned in an ultrasonic bath; subsequently, the AZP4620 photoresist (with a thickness of 7～8 μm) was spun (with spin speed of 6000 RPM) onto the silicon wafers. Then, the photoresist film was placed on a hotplate and baked at 100 °C for approximately 1 min. The resist film was exposed based on a mask aligner (IMP SF-100). Following the development process, the resist film with micro-pillars was baked at 100 °C for 2 min, and then etched using the DRIE (Bosch) process for approximately 95 min. Finally, the designed meta-atoms with different shapes were obtained after removing the photoresist by using acetone.

Near-field scanning THz time-domain spectrum microscopy system (NSTM)—The NSTM was built based on a traditional THz time-domain spectrum system (THz-TDS). The traditional detector in the THz-TDS in our NSTM was replaced as a THz tip that can be scanned in three-dimensional space. The incident femtosecond laser with a centre frequency of 780 nm was split into two parts: one part of the femtosecond laser was impinged on the photoconductive antenna to radiate the THz waves that interacted with the fabricated samples, while the other part of the femtosecond laser was coupled into a single-mode fiber and shined onto the THz tip that was mounted on a three-dimensional translation stage. The metasurface devices were fixed after the photoconductive antenna, and the THz tip was scanned inside the focusing region to reveal the electric-field intensity and phase distributions of the samples. The optical setup is shown in the supplementary materials of Section 7 of Fig. S11.

This work is supported in part by the National Key Research and Development Program of China (2017YFA0701005), National Natural Science Foundation of China (62271320, 61871268), “Shuguang” Program of Shanghai Education Commission (19SG44), and the 111 Project (D18014).