Fine 3D control of THz emission in air with dual femtosecond laser pre-pulses at tunnelling ionisation regime

Two-pulse experiment with pre- and main pulses²⁷ revealed the required timing and spatial separation for the shocked-compressed air by the pre-pulse to be pushed into the position of the main pulse at $ (x,y) = (0,0) $ for the maximum emission of THz radiation. Pre-pulse had to arrive 9.7 ns earlier to the focus of the main pulse from the position $ \Delta y\sim 33\; {\text{μm}} $ away for the maximum THz emission. Polarisation of THz radiation was found aligned along the direction of focal positions of pre-pulse and main pulse²⁷. Here, we add a second pre-pulse of the same 0.2 mJ energy, which arrives at the same time as the first pre-pulse, with the possibility of placing it freely in 3D space $ (x,y,{\textit z}) $. Fig. 1 shows the scheme of the experiment and the diagnostics. Details of the experimental setup and the measurement methodology are described in Sec. “Materials and methods”. The effect of placement of the second pre-pulse on polarisation and intensity of THz radiation was systematically studied. Due to short 35 fs pulse (~120 μm in length) and z-position (along the beam propagation) change only tens-of-micrometers. Hence, the timing of both pre-pulses can be considered simultaneous, regardless of the actual z-coordinate of the pre-pulse 2 within an error of ~0.1 nm, which is by an order of magnitude smaller than the shockwave thickness.

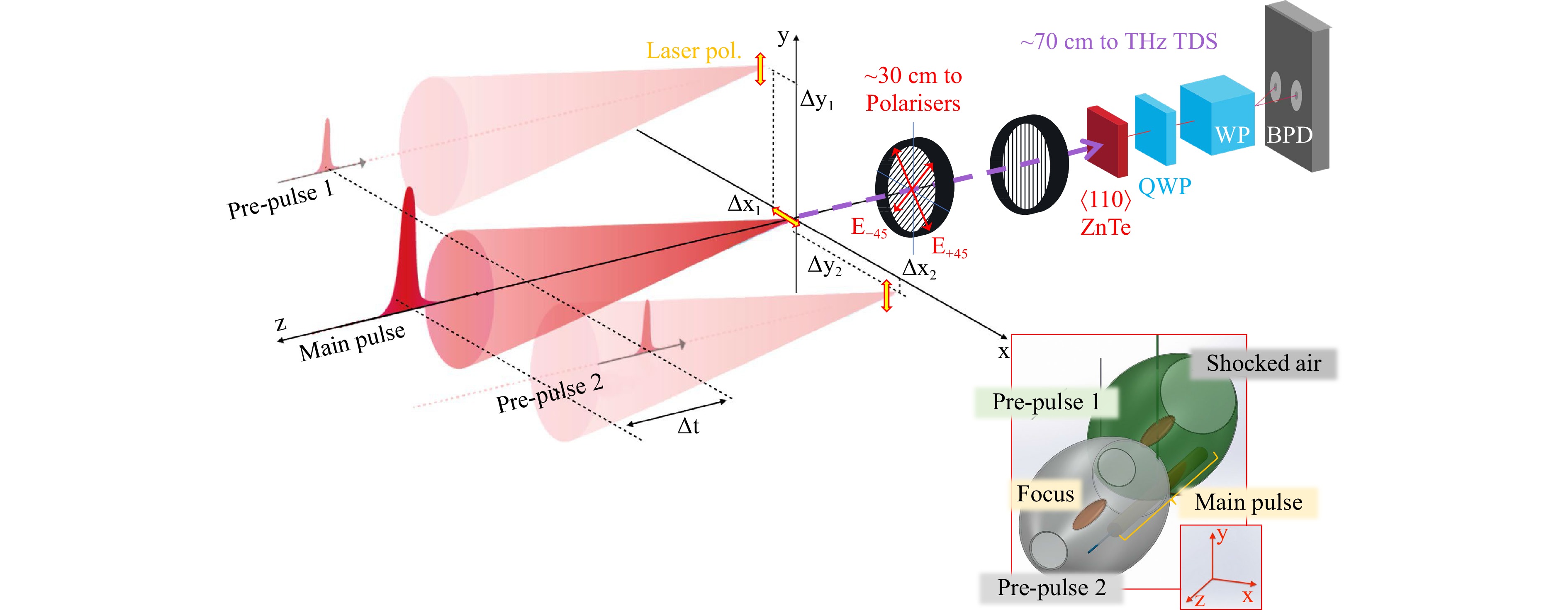
Fig. 1  Schematic diagram of the experimental setup with temporal ($ \Delta t $ = 9.7 ns) and spatial offsets of the the pre-pulse 1 ($ \Delta x_1 $, $ \Delta y_1 $, $ \Delta {\textit z}_1 $), and the pre-pulse 2 ($ \Delta x_2 $, $ \Delta y_2 $, $ \Delta {\textit z}_2 $) irradiation positions. THz electrical fields $ E_x, E_y $ are calculated from $ E_{+45} $ and $ E_{-45} $ measurements, where $ \pm 45^\circ $ is the angle of the polariser wire-grids set out for the polarisation measurement: $ E_x=E_{+45}+E_{-45} $ and $ E_y=E_{+45}-E_{-45} $. The pre-pulse position was also tuned to place focus at the up-stream (positive $ \Delta {\textit z} > 0 $) and down-stream $ \Delta {\textit z} <0 $ locations; see bottom-right inset. The standard polarised THz-TDS detection system was based on a pair of wire-grid polarisers in front of ZnTe crystal, a quarter-wave plate (QWP), a Wollaston prism (WP) and a balanced photo-detector (BPD). Lower-inset shows 3D positions of the focal region of both pre-pulses with shock-wave fronts (geometry is based on optical shadowgraphy imaging).

$ Y $-position of pre-pulse 2 Fig. 2 shows the emission of THz radiation ($ E_y $ component) for the situation when the pre-pulse 1 is focused at $ \Delta y = +33\; {\text {μm}} $. At the same time, the second pre-pulse is focused at other $ (0,\pm y) $ position with respect to the main-pulse focus at $ (x,y)=(0,0) $; see Fig. 1. Change of $ E_y $ field orientation was observed over the measured range of THz frequencies as shown by the time domain transients in Fig. 2a. When two pre-pulses were simultaneously irradiated at opposite (with respect to $ y=0 $) positions, the cancellation of THz $ E_y $ components occurred. This confirms that the air density gradient induced by the shock front is more important than the air mass density, which is increased by two colliding shocks.

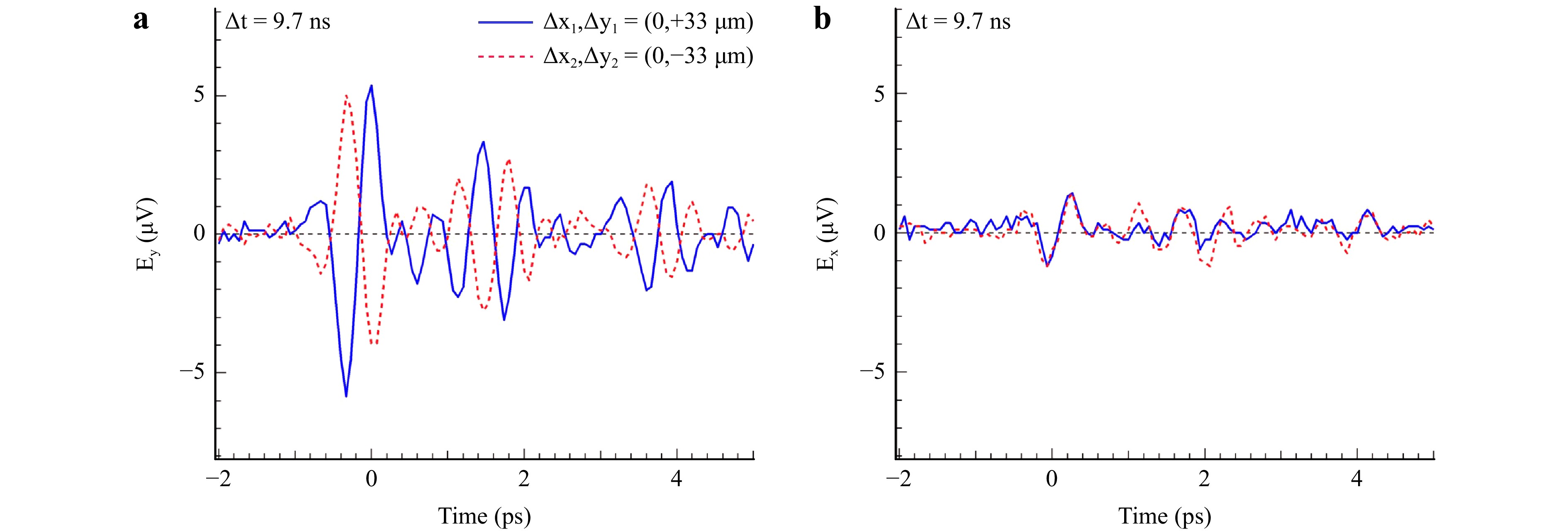
Fig. 2  The THz-TDS waveforms of a $ y $-component $ E_y $ of the single pre-pulse when the delay time between the pre-pulse and main pulse irradiation is at 9.7 ns. The spatial offset for the pre-pulse irradiation is ($ \Delta x $, $ \Delta y $) = ($ 0\; {\text μ} $m, $ +33\; {\text μ}$m) for the blue solid line or ($ 0\; {\text μ} $m, $ -33\; {\text μ}$m) for the red dotted line. b The $ x $-component $ E_x $ of the dual pre-pulses when ($ \Delta x_1 $, $ \Delta y_1 $, $ \Delta {\textit z}_1 $) = ($ 0\; {\text μ} $m, $ +33\; {\text μ}$m, $ 0\;{\text μ} $m) and ($ \Delta x_2 $, $ \Delta y_2 $, $ \Delta {\textit z}_2 $) = ($ 0\; {\text μ} $m, $ -33\; {\text μ} $m, $ 0\; {\text μ} $m).

For two pre-pulse experiments, a dependence of THz emission on the offset $ \Delta y_2 $ of the second pre-pulse was determined. The delay of the first pre-pulse of 9.7 ns was optimised, so the THz emission was the most intense. The THz intensity is calculated from the $ (E_x,E_y) $ components as peak-to-peak value (see inset in Fig. 3). A pictorial diagram for each irradiation point is presented by the projection of THz E-field on $ (E_x,E_y) $-plane. The projection shows the overall temporal evolution of THz electric field orientation during emission time.

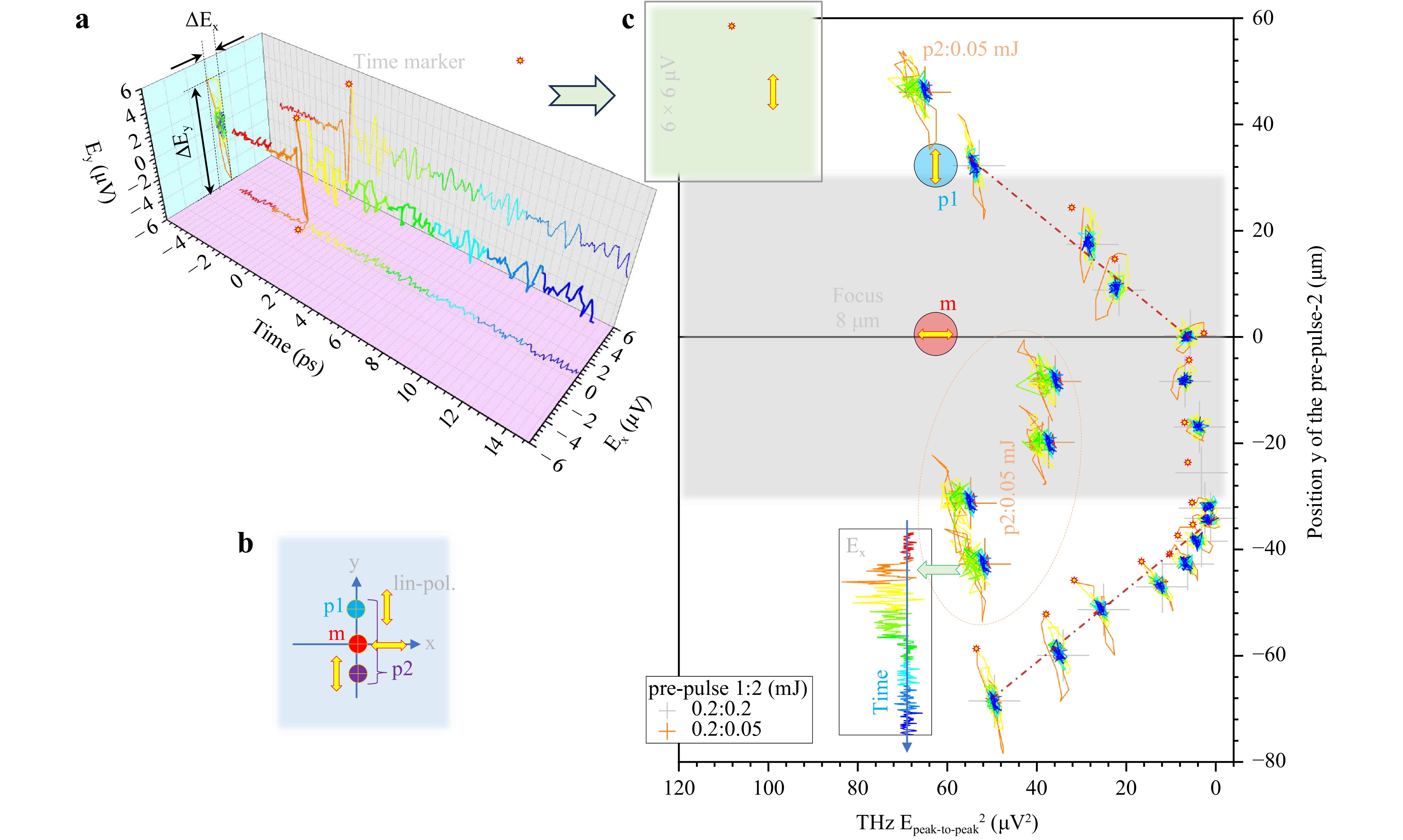
Fig. 3  a THz polarisation evolution in time shown as a $ (E_x,E_y) $ map. b Geometry of main pulse (m) and pre-pulses 1,2 (p1,p2). Pre-pulse 1 and the main pulse were fixed, and pre-pulse 2 was scanned along the $ y $-axis. c The THz-polarisation $ |E_{{\rm{peak}}-{\rm{to}}-{\rm{peak}}}|^2 $ intensity as a function of the vertical offset for the second pre-pulse, $ \Delta y_2 $. $ |E_{{\rm{peak}}-{\rm{to}}-{\rm{peak}}}|^2 $ is as shown in the inset and is equal to $ |\Delta E_x|^2 $ + $ |\Delta E_y|^2 $. The delay time between the pre-pulse and main pulse irradiation is 9.7 ns. The spatial offset for the first pre-pulse irradiation is fixed at ($ \Delta x_1 $, $ \Delta y_1 $) = ($ 0\; {\text μ} $m, $ +33\; {\text μ} $m) while the position of the second pre-pulse irradiation, $ \Delta y_2 $ and $ \Delta x_2 $ was varied from 0 to $ 30\; {\text μ} $m. The blue THz-pol. plot indicates the results from two pre-pulse irradiation with both pre-pulses at 0.2 mJ. The black THz-pol. plot indicates the results from two pre-pulse irradiation with the pre-pulses at 0.2 mJ and the second pre-pulse at 0.05 mJ. The red THz-pol. plot indicates single pre-pulse irradiation condition with the pre-pulse at 0.2 mJ and ($ \Delta x $, $ \Delta y $) = ($ 0\; {\text μ} $m, $ +33\; {\text μ} $m). The main pulse energy is 0.4 mJ. The red dotted line indicates the THz emission from a single main pulse irradiation in air.

One pre-pulse produced enhancement of THz emission by 13 times, i.e., the value $ |E_{{\rm{peak}}-{\rm{to}}-{\rm{peak}}}|^2 = 53\; {\text μ} $V² compared to the value $ |E_{{\rm{peak}}-{\rm{to}}-{\rm{peak}}}|^2 \approx 4\; {\text μ} $V² without a pre-pulse. The $ E_y $ component of the THz field becomes larger for offsets $ |\Delta y_2|>33\; {\text μ} $m compared to the enhancement produced by the first. Conversely, when pre-pulse 2 was closer to the position $ (0,0) $ where the main pulse is focused, the amplitude of THz field was reduced.

The second pre-pulse of four times smaller energy of 0.05 mJ, had no significant effect on the THz emission, regardless of the position at $ y<0 $, opposite side from pre-pulse 1 with respect to the main pulse focus. A different evolution in time for such 0.05 mJ second pre-pulse was observed. It showed a $ \sim 6 $ ps duration of larger negative values of $ E_x $ component (see inset in Fig. 3c and colour asymmetric $ (E_x,E_y) $ markers). This is probably due to a later arrival and shorter contribution of a shock wave triggered by a four times lower pre-pulse energy. Indeed, the radius $ R $ of a cylindrical shock wave created by the laser energy deposition on the axis $ E_p $ increases with time $ t $ as $ R(t)\propto E_p^{1/4}\sqrt{t} $ according to the Sedov–von Neumann–Taylor model²⁹. The major contribution to the THz enhancement was governed by the first pre-pulse with an energy of 0.2 mJ.

Interestingly, when pre-pulse 2 was on the same side as pre-pulse 1 at a distance from the main pulse position larger than 33 μm (pre-pulse-1), the $ E^2 $ enhancement was $ \sim 15 $ times (see Sec. “Theoretical description of light-air interaction and THz emission” for discussion). In this case, the shock-affected volume from the pre-pulse 1 was crossed by the pre-pulse 2. When a shock wave propagates through a region of rarefied density $ \rho_1 $ formed by the other pre-pulse, the same cylindrical explosion model predicts scaling $ R\propto\rho_1^{-1/4} $. When pre-pulse 2 arrived at $ y = 0 $ to $ -33\; {\text μ} $m (the opposite side of the $ y $-axis as compared to pre-pulse 1), it quenched the effect of THz enhancement. However, at even more negative positions of pre-pulse 2, the same enhancement was observed for arriving shocks to the position of the main pulse; see red dot-dashed line drawn as eye guides in Fig. 3c.

$ X $-position of pre-pulse 2 Next, the dependence of THz emission of the $ x $-position of the second pre-pulse was determined, see Fig. 4. The $ (E_x,E_y) $ trajectories indicate the radial influence of the pre-pulse irradiation position with respect to the main pulse (the pre-pulse 1 was always at the $ (0,33)\; {\text μ} $m). The ellipticity of THz polarisation was larger for the pre-pulse 2 locations (larger $ |\Delta x_2| $). This is explained by the optimal timing of 9.7 ns for the pre-pulse position at $ \sim 33\; {\text μ} $m from the main pulse position. This is valid along any direction perpendicular to beam propagation in the $ (x,y) $ plane. When $ |x_2|<33\; {\text μ} $m, the shock arriving along the $ x $-axis does not fit the perfect timing for THz enhancement and alters the effect of the pre-pulse 1 arriving along a perpendicular direction. When $ |x_2|>33\; {\text μ} $m, pre-pulse 2 makes a small contribution to the enhancement determined by pre-pulse 1. The pre-pulses 1 and 2 arriving at perpendicular directions define the ellipticity of the THz radiation and its handedness (see Fig. 4). The duration of the most intense THz radiation lasts approximately one cycle, corresponding to $ 2{\text π} $ rotation in the $ (x,y) $ plane (see a side-view cross-section along the time axis in the inset of Fig. 4).

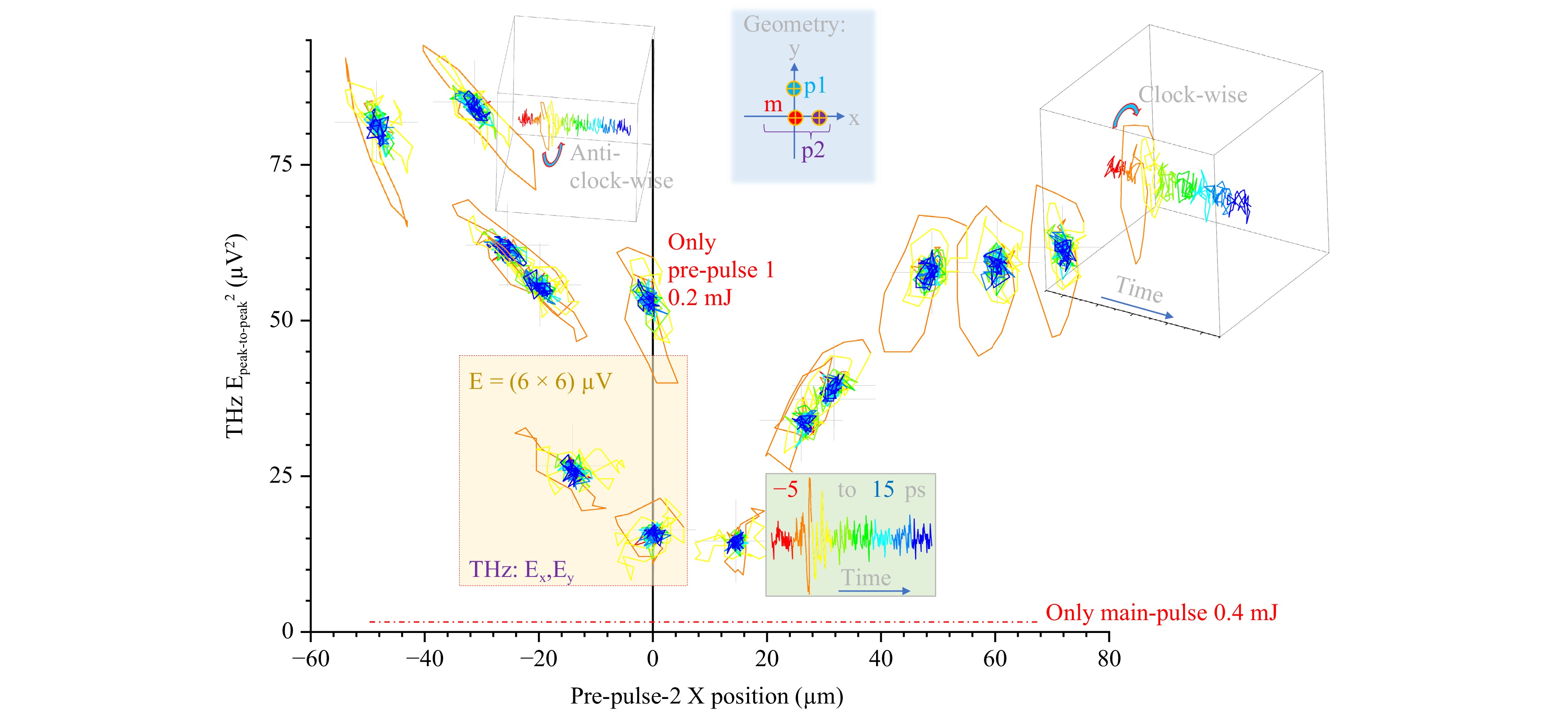
Fig. 4  The THz-polarisation $ |E_{{\rm{peak}}-{\rm{to}}-{\rm{peak}}}|^2 $ [μV²] intensity as a function of the horizontal offset for the second pre-pulse, $ \Delta x_2 $. The delay time between the pre-pulse and the main pulse is 9.7 ns. The spatial offset for the first pre-pulse irradiation is ($ \Delta x_1 $, $ \Delta y_1 $) = ($ 0\; {\text μ} $m, $ +33\; {\text μ} $m), while the second pre-pulse is focused at different $ \Delta x_2 $ position with $ \Delta y_2 $ = $ 0\; {\text μ} $m (see top-right inset for geometry schematics). The RGB projections ($ E_x,E_y $) of THz plots are from two pre-pulse irradiation with both pre-pulses at 0.2 mJ. The THz-pol. plot, when the pre-pulse is at 0.2 mJ and ($ \Delta x $, $ \Delta y $) = ($ 0\; {\text μ} $m, $ +33\; {\text μ} $m), indicates single pre-pulse irradiation condition with the main pulse energy is at 0.4 mJ. The red dotted line indicates the THz emission from single main pulse irradiation in air at $ E^2\approx 4\; {\text μ} $V². The boxed-area (yellow) is $ 6\times 6\; {\text μ} $V for the $ (E_x,E_y) $-projection maps located at the cross-markers, at which the total intensity $ |E_{{\rm{peak}}-{\rm{to}}-{\rm{peak}}}|^2 = E_x^2 +E_y^2 $ is plotted after power calibration. The 3D projection insets illustrate RGB time evolution over a span −5 ps to 15 ps and reveal the sense of polarisation rotation (looking into the beam or time axis); it is plotted for the closest projection RGB markers, respectively.

The dependence of THz emission on the position of the pre-pulse along the z axis is presented in Appendix “Z-position of pre-pulse 2”.

Laser air ionisation and electron heating Here, a physical scenario of air breakdown by the pre-pulse and main pulse and the dynamics of the plasma formation are analysed. The laser pulse parameters, the air ionisation potentials and the main experimental results are summarised in Appendix “Input parameters and experimental results for theoretical estimations”.

Laser focusing in our experiment was carried out with an off-axis parabolic mirror with an effective numerical aperture $ NA = 0.125 $ as determined from direct imaging of water-jet breakdown³⁰. The focal spot area is estimated from the Airy disk radius $ w_0=0.61\lambda/NA\approx 3.9\; {\text μ} $m, which is close to optical observation by shadowgraphy at low pulse energies. The axial extension of the air breakdown zone in the experiment is $ \sim 120-150\; {\text μ} $m ²⁷. It is close to the depth-of-focus $ 2{\textit z}_R $, where the Rayleigh length $ {\textit z}_R = \pi w_0^2/\lambda \approx 60\; {\text μ} $m. The focusing volume is considered as a cylinder of length $ 2{\textit z}_R $, radius $ w_0 $ and volume $ V_{\rm{las}} =5.7\times 10^{-9} $ cm³.

The energy of the pre-pulse $ E_1=0.2 $ mJ and the main-pulse $ E_m=0.4 $ mJ correspond to the intensity $ 1.2\times 10^{16} $ W/cm² and $ 2.4\times 10^{16} $ W/cm², respectively. Under these conditions, the laser ponderomotive potential is much larger than the ionisation potential of atoms, the air is ionised in the tunnelling regime, and a plasma is created in the focusing volume.

The plasma creation is estimated for the air consisting of 20% of oxygen and 80% of nitrogen molecules. The ionisation rate $ w_i(E) $ as a function of laser electric field $ E(t) $ and atomic charge $ i $ is taken according to the Ammosov-Delone-Krainov (ADK) theory³¹. For the sake of simplicity, we assume a consecutive ionisation from unperturbed atomic levels.

Electron ionisation and heating are described by the kinetic equation for the distribution function of free electrons, $ f_e=\sum\limits_j f_{e,j} $, where $ f_{e,j} $ is the electron partial distribution function corresponding to the atom ionisation from the $ j $-level:

where $ f_{e,j} $ is normalised by the density of neutral atoms, $ n_a $, $ E(t) $ is the laser electric field, $ n_{e,j}= \int dv\,f_{e,j} $ is the probability of ionisation from the level $ j $, $ \delta({\bf{v}}) $ is the delta function and $ {\bf{v}} $ is velocity. In the case of linear polarisation, non-relativistic electric field, and neglecting electron collisions, the electrons are moving in the direction of the laser field, and the distribution function is one-dimensional.

This equation describes the production of free electrons and their energy increase. The energy is taken from the laser field; therefore, the laser absorption and atom ionisation proceed simultaneously. Integrating kinetic equation, one obtains equations for the three moments of electron distribution function, $ n_{e,j} $, $ n_{e,j} v_{e,j}=\int dv\,v\,f_{e,j} $ and $ n_{e,j} v_{e,j}^2 =\int dv\,v^2 f_{e,j} $:

These equations are solved numerically using Wolfram Mathematica package for each ionisation level and each atom separately, and the average ionisation and the average residual electron energy are evaluated as

Two examples of numerical solutions are shown in Fig. 5 for $ j=2 $ (left) and $ j=5 $ for the main pulse and the nitrogen atom. The electron residual energies are on the order of ionisation potential and significantly smaller than the ponderomotive energy. This is in agreement with the theoretical analysis³².

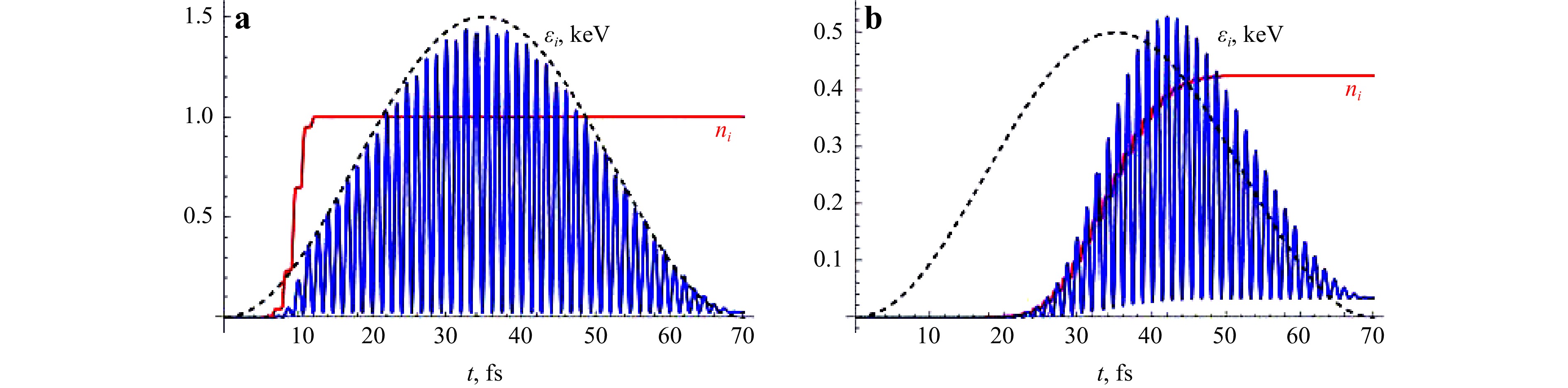
Fig. 5  Ionisation probability (red) and the electron kinetic energy for the parameters of the main pulse interacting with the nitrogen ion and liberation an electron from the level $ j=2 $ (left) and 5 (right). Pulse duration is 35 fs at FWHM; it is shown with the dashed lines.

The total ionisation energy per atom (assuming 80% nitrogen + 20% oxygen), the number of free electrons per atom, and the residual average electron energy are: for the pre-pulse $ \varepsilon_{\rm{ion}}=127.2 $ eV, $ Z_e=4.06 $, and $ \varepsilon_e=35.7 $ eV; for main pulse $ \varepsilon_{\rm{ion}}=244.8 $ eV, $ Z_e =4.85 $, and $ \varepsilon_e= 74.0 $ eV. Multiplying the total energy loss per ion, $ \varepsilon_{\rm{tot}}= \varepsilon_{\rm{ion}}+ Z_e\varepsilon_e $, by the ion density and the focal volume, we obtain the free electron density and the laser energy loss for ionisation and electron heating. For the pre-pulse propagating in the air at normal conditions, the electron density is $ n_e=Z_e n_a= 2.2\times 10^{20} $ cm⁻³ and the energy loss is $ \varepsilon_{\rm{tot}} n_a V_{\rm{las}}= 13.4\,{\text μ} $J. The main pulse is propagating along the shock front in compressed air. The compression factor $ C_r = 5.4 $ was measured in Ref. 27. Therefore, the electron density in the focal zone is $ n_e = 2Z_e C_r n_{\rm{air}} = 1.4 \times 10^{21} $ cm⁻³, and the laser energy loss is $ \varepsilon_{\rm{tot}} C_r n_a V_{\rm{las}} = 160.9\,{\text μ} $J.

Laser collisional absorption In addition to the ionisation energy loss, the laser pulse transfers its energy to electrons due to the electron-ion collisions. As it is a weaker effect, we account for it as an addition to ionisation using standard expressions for the electron collision frequency $ \nu_e $ and Coulomb logarithm $ \Lambda_e $³³:

where the $ n_e=Zn_{a} $ is the electron density in cm^-3 and electron temperature is in eV. For estimates of the collision frequency during the laser pulse, we account for the electron quiver velocity being larger than the electron thermal velocity. According to Ref. 34, under such conditions, the electron-ion collision frequency depends on the electron ponderomotive energy instead of the electron temperature. Conversely, after the end of the laser pulse, the electron energy is strongly reduced, and the collision frequency increases. The electron distribution is isotropized on a time scale of less than 1 ps. Since that time is shorter than the time of THz emission, we assume that electron energy is equally distributed in three directions and take $ T_e $ as two-thirds of the residual electron energy.

For the pre-pulse, the electron collision frequency $ \nu_e =0.95 $ ps⁻¹, and the fraction of laser energy lost is 0.4%, which corresponds to the electron energy gain of $ 0.84\,{\text μ} $J. For the main pulse, assuming that air is compressed 5.4 times, the electron collision frequency $ \nu_e=2.5 $ ps⁻¹, the fraction of laser energy lost is 7.2% and the electron energy gain is $ 28.7\,{\text μ} $J.

Combining the ionisation energy, residual electron energy, and collisional heating for the pre-pulse, we estimate the total energy loss of $ 14.3\,{\text μ} $J, electron density $ 2.2\times 10^{20} $ cm⁻³ and electron temperature of 26.6 eV. Collisional heating contributes about 10% to the electron temperature at the end of the laser pulse. The electron collision frequency is 72.6 ps⁻¹, so isotropisation proceeds very rapidly after the end of the laser pulse.

For the main pulse, the total absorbed laser energy is $ 189.6\,{\text μ} $J, the electron density is $ 1.4\times 10^{21} $ cm⁻³, and the electron temperature is 64.1 eV. Collisional heating contributes about 23% to the electron temperature at the end of the laser pulse. The electron collision frequency is 147.4 ps⁻¹.

Propagation of the heat wave and shock formation After the laser pre-pulse, the thermal energy in plasma is $ 8\,{\text μ} $J. It is larger but comparable to the shock energy measured in the experiment. The plasma pressure is 9.3 kbar. It leads to plasma expansion and the formation of a cylindrical shock on a time scale of a few hundred ps. According to the measurements²⁷, the shock propagates a distance of $ 33\,{\text μ} $m in 10 ns, and the air compression in the shock front is $ \rho/\rho_0\simeq 5.4 $, which is slightly less than the maximum compression $ (\gamma+1)/(\gamma-1)=6 $ for the air adiabat $ \gamma=1.4 $.

The parameter that defines the shock formation is $ \kappa_{e0}/c_{s0}w_0 $ where $ \kappa_{e0}= 4500 $ cm²/s is the electron heat conductivity, and $ c_{s0}= 13 $ km/s is the sound velocity. (See details of derivation in Appendix. "Propagation of the heat wave and shock formation". The shock formation time is 650 ps, and the initial shock position is $ 8.7\,{\text μ} $m. The initial shock velocity is $ c_{s0} (\kappa_{e0}/c_{s0}w_0)^{-1/5}=7 $ km/s, which corresponds to the Mach number $ M\simeq 20 $. These values are the initial conditions for the cylindrical shock that can be described by the Taylor-Sedov formula: $ r(t) = r_s (t/t_s)^{1/2} $. The Mach number decreases as a square root of time.

The thickness of the shock front is needed for further analysis of mechanisms of electromagnetic emission. A general theory of shock waves predicts the front width on the order of a few molecule mean free paths²⁹. A more detailed analysis³⁵ of the shock in air evaluates the front thickness as $ 2.5-3 $ mean free paths for the shock Mach number $ M\gtrsim 3 $. The mean free path of a molecule in air at normal conditions is $ 0.066\,{\text μ} $m. Consequently, we take the shock front thickness $ d_{\rm{sh}} = 0.2\,{\text μ} $m as a reference value.

The authors of Ref. 36 have reported on the studies of shock excitation in air under conditions similar to our experiment. They used a 0.5 PW/cm², 360 fs pulses at 1030 nm wavelength focused by $ NA = 0.4 $ objective lens and showed initiation of air breakdown along $ \sim 10\; {\text μ} $m long focus. A shock wave formation started 0.1 ns after the shot. The experimentally determined threshold intensity of the air breakdown was 80 TW/cm². Experimental results of shock wave propagation are well fitted by the equation of state of air $ P=(\gamma-1){\cal{E}}_{in} \rho/\rho_0 $, where $ {\cal{E}}_{\rm{in}} $ is the internal energy per unit volume, which is driving explosion. Initial pressures reaching kbar level were reduced to tens of bar after propagation of a few micrometers; the Mach number $ \sim30 $ and velocity of shock wave were determined from a side view imaging. This paper also shows that a tighter focusing can localise the shocked region to small volumes within cross-sections of tens-of-μm³⁶ and are promising for sub-wavelength sources of THz radiation. These conditions are similar to our study.

Diffusion currents Since the electromagnetic emission is produced on a time scale larger than the electron collision time, the electron inertia can be neglected, and Ohm's law describes the current excitation after the end of the laser pulse:

where the first term on the right-hand side describes the electric resistivity due to electron collisions, $ \eta_e=m_e \nu_e/e^2 n_e $, and the second term represents the source related to the gradient of the electron pressure $ n_eT_e $.

The main laser pulse propagates parallel to the shock front, along the z-axis, and it is perpendicular to the direction of shock wave propagation, which is along the $ x $-axis, see Fig. 6. The density profile in the shock front $ n_{e0}(x) $ is asymmetric: it has a fast rise at the front side and a slow decrease at the rear side.

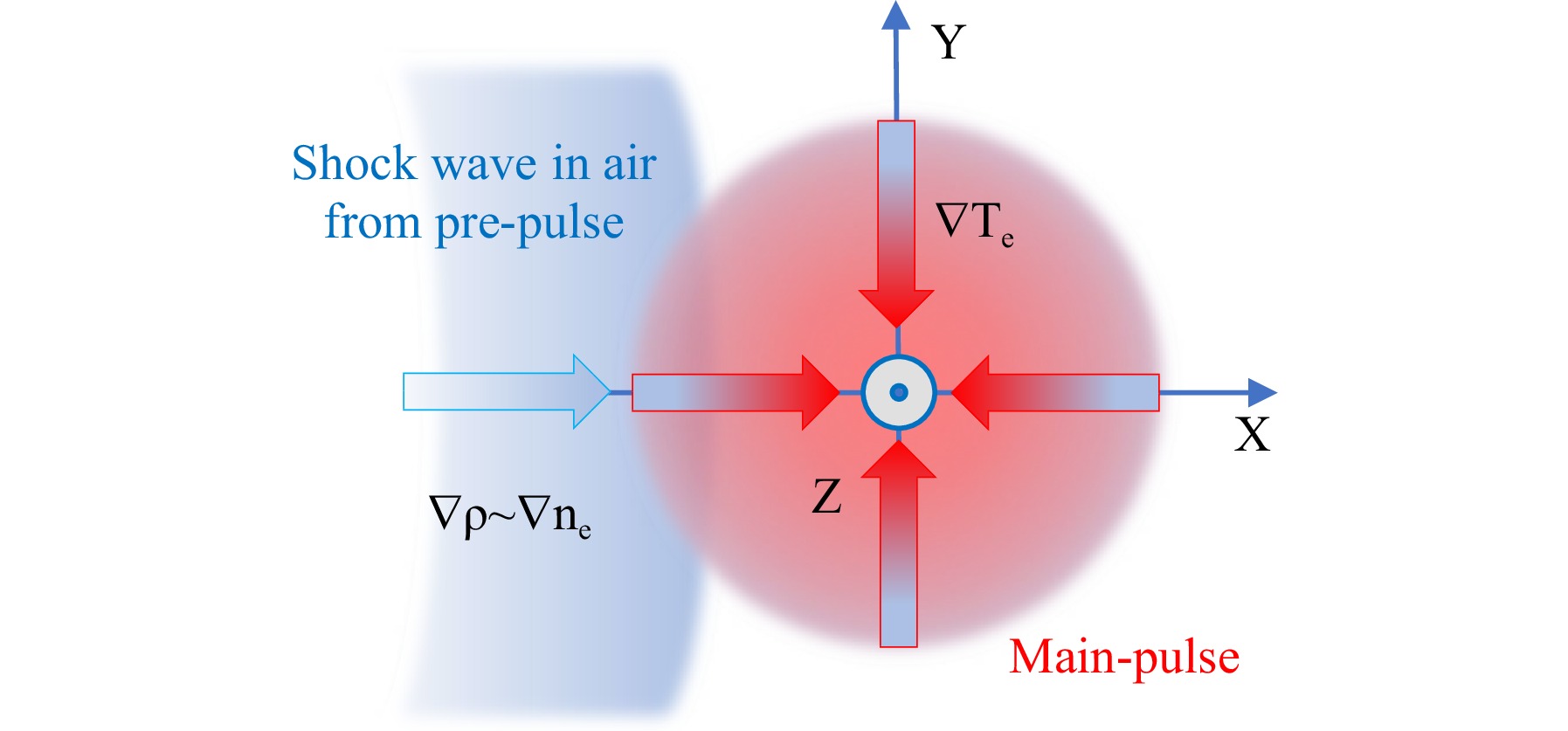
Fig. 6  Two-pulse enhancement of THz generation in air by the spontaneous magnetic field $ B_{\textit z} $ due to coupled non-parallel gradients of $ \nabla T_e $ and $ \nabla n_e $.

The electron temperature is also inhomogeneous; it is larger on the laser axis and decreases with the radius $ r =\sqrt{x^2 +y^2} $ in the plane $ (x,y) $ perpendicular to the laser propagation direction. Since the electron density and temperature gradients are non-parallel, the electric current has two components: an electrostatic component in the direction of the pressure gradient and a rotational component, which generates a magnetic field perpendicular to the density and temperature gradient. These currents are considered in the next two sections.

Electrostatic diffusion current. The electrostatic current is associated with the charge density perturbation described by the continuity equation $ e\partial_t n_e=\nabla\cdot {\bf{j}} $. Inserting in this equation expression for the current from Eq. 5 and using the Poisson equation for the electric field, $ \epsilon_0 \nabla\cdot {\bf{E}}=e(n_i- n_e) $, we obtain the following equation for the electron density:

where $ D_e =T_e/m_e \nu_e $ is the electron diffusion coefficient and $ \omega_{\rm{pe}} $ is the electron plasma frequency. This equation describes the generation of an electrostatic field due to the diffusion of electrons heated by the laser pulse, which is similar to the photo-Dember effect in semiconductors^{37, 38}. Before the laser pulse arrival, the air is neutral. The laser pulse creates free electrons and heats them. Under the pressure gradient, the electrons start moving, while the ions are left behind because of their large mass. Therefore, the electron mobility creates an electric current, which induces the charge separation and electric field. Eventually, the electron diffusion stops when the pressure gradient is compensated by the electrostatic field.

We neglected in Eq. 6 excitation of plasma oscillations assuming that the time of electron heating equal to the laser pulse duration (about 30 fs) is much longer than the plasma wave period, $ 2\pi/\omega_{\rm{pe}} $, which is about 3 fs. The value of the charge separation, $ \delta n_e=n_e -Z_en_i $, is estimated by comparing the second term on the left-hand side, $ D_e n_{e0}/d_{\rm{sh}}^2 $ with the term on the right-hand side. The value of charge separation is $ \delta n_e/n_{e0} \simeq \lambda_{\rm{De}}^2/d_{\rm{sh}}^2 $, where $ \lambda_{\rm{De}}= (\epsilon_0 T_e/e^2n_e)^{1/2} $ is the electron Debye length. Since the Debye length in the experiment is on the order of 1 nm, about two orders of magnitude smaller than the shock front thickness, the charge separation of very small, about four orders of magnitude smaller than the plasma density. Therefore, Eq. 6 can be linearised and written for $ \delta n_e=n_e -Z_en_i $:

The second term on the right-hand side drives the charge separation because the diffusion coefficient increases with time during the laser heating. The first term on the right-hand side accounts for the charge relaxation due to collisions. This time of the charge relaxation can be estimated by comparing the term on the left-hand side of Eq. 7 with the first term on the right-hand side. This time is much shorter than 1 ps. So, the time derivative on the left-hand side can be neglected; that is, the charge separation is almost instantaneously accommodated to the laser heating and $ \delta n_e = \lambda_{\rm{De}}^2 \nabla^2n_{e0} $. The strength of the saturated electric field is $ E_s \simeq T_e/e d_{\rm{sh}} \simeq 3 $ MV/cm is quite large, but no current is created.

This analysis confirms that electron diffusion cannot produce electromagnetic emission in the experiment.

Rotational diffusion current. The mechanism of generation of the rotational component of electric current is illustrated in Fig. 6. It is called the Biermann battery effect^{39, 40} in plasma physics. The crossed gradients of temperature and density induce a rotational electric current, which is not related to the charge separation and evolves on a longer timescale. The current is related to the magnetic field by Ampere's equation, $ {\text μ}_0{\bf{j}}=\nabla\times{\bf{B}}_s $. The equation for the magnetic field is obtained by taking the curl of Ohm’s Eq. 5 and using Faraday's equation for the curl of the electric field:

(We assume here a constant resistivity.) Since the gradients of the temperature and density on the right-hand side are in the $ (x,y) $ plane, the diffusion proceeds in that plane, and only z-component of the magnetic field is generated.

The characteristic time of magnetic field generation, $ t_{\rm{dif}}=w_0^2{\text μ}_0/\eta_e $, is found by comparing the two terms in the left-hand side of this equation. The value of the magnetic field after the saturation is estimated by comparing the second term on the left-hand side with the term on the right-hand side: $ eB_0=T_e {\text μ}_0 w_0/d_{\rm{sh}}\eta_e $, and the estimate of the current follows from the Ampere equation: $ j_x \simeq T_e/e d_{\rm{sh}}\eta_e $.

The magnetic field is approximated in the polar coordinates $ (r,\varphi) $ as $ B_s= B_0 \sin\varphi\, b(t,r) $ where $ b(r,t) $ describes the radial profile of magnetic field:

This equation is obtained from Eq. 8 by multiplying it by $ \sin \varphi $ and integrating over $ \varphi $ from 0 to $ 2{\text π} $, assuming that $ w_0 \gg d_{\rm{sh}} $. Eq. 9 is solved numerically using Wolfram Mathematica package with the initial condition $ B_s(t=0)=0 $ by considering a Gaussian distribution for the temperature, $ T_e(r)=T_{e0}\exp(-r^2/w_0^2) $, and an exponential density profile, $ n_e(x) =2n_{e0}/[1+\exp(x/d_{\rm{sh}})] $. The coordinate origin corresponds to the axis of the main pulse. The left panel in Fig. 7 shows the dependence of the dimensionless function $ b(r,t) $ on the radius and time. The magnetic field increases linearly with time for $ t\lesssim t_{\rm{dif}} $, and then it is saturated at the level $ b_{\max}\simeq 0.14 $. The radial profile has a maximum at $ r\simeq w_0 $. The spatial distribution of the magnetic field in the plane $ (x,y) $ perpendicular to the laser propagation direction is shown in the right panel in Fig. 7. It has a dipole structure with a positive lobe for $ y>0 $ and a negative lobe for $ y<0 $. So, the average magnetic field is zero. The lines of constant magnetic field correspond to the current streamlines. The current is directed along the $ x $ direction near the axis, and the current loops are closed. An approximate analytical expression for the magnetic field is given in Appendix. “Approximate solution for the magnetic field generated at the shock front”.

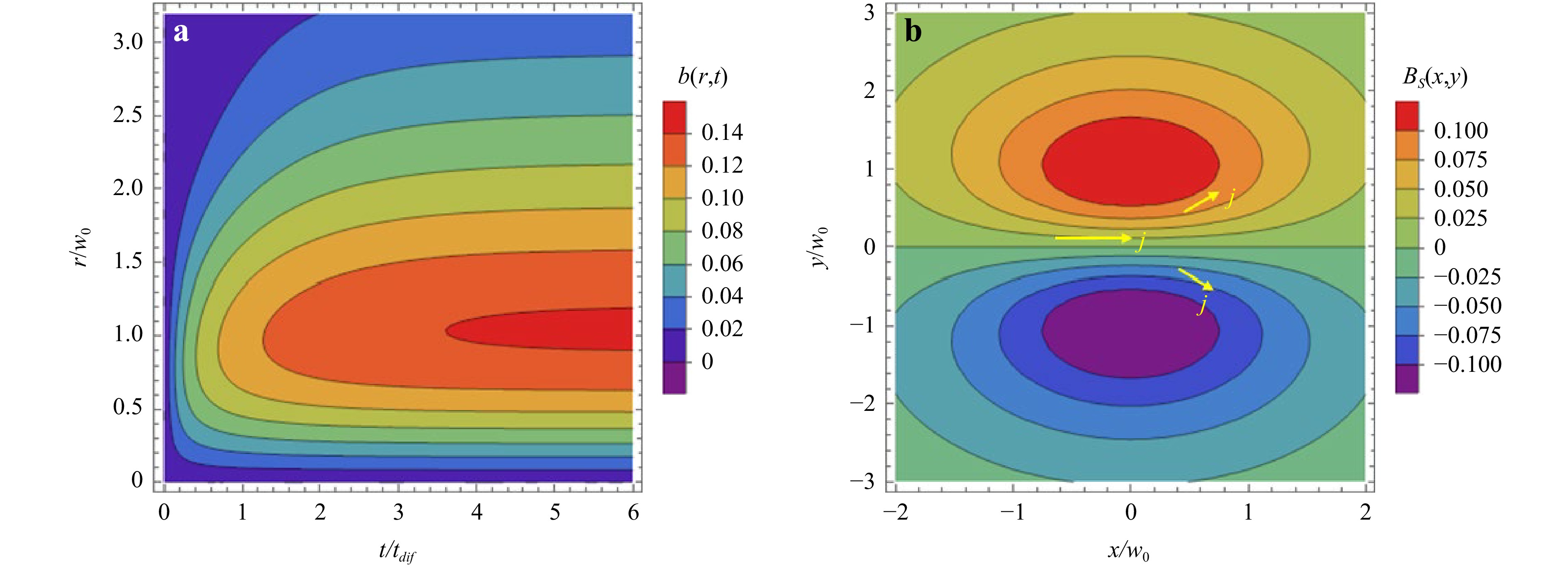
Fig. 7  a Time and radial dependence of the dimensionless function $ b(r,t) $ obtained from a numerical solution of Eq. 9. b Distribution of the magnetic field in the plane $ (x,y) $ obtained from the solution of Eq. 8 at time $ t=t_{\rm{dif}} $. Arrows show the direction of the electric current. The origin $ x=0 $ and $ y=0 $ correspond to the laser beam axis and the maximum of the plasma density gradient.

For the parameters of the main pulse and for the air compression $ C_r=5.4 $, we find the diffusion time $ t_{\rm{dif}} = 4.7 $ ps, the maximum value of the magnetic field $ B_{\max}=b_{\max}B_0=54 $ T and the maximum current density $ j_{\max}=1.2 $ GA/cm². The lifetime of that current and magnetic field is limited by heat diffusion. It is evaluated in the preceding section to be on the order of a few hundred ps. Performing integration over the focal volume for $ t\gg t_{\rm{dif}} $, we obtain the energy of the magnetic field after the saturation: $ W_B\simeq B_{\max}^2 V_{\rm{las}}/2{\text μ}_0 $. For our parameters, the total magnetic energy is about $ 6.6\,{\text μ} $J. This sets the upper limit of the emitted electromagnetic energy.

Electromagnetic emission Electromagnetic emission can be deduced from the general formula for the vector potential induced by the time-dependent current,

where $ t'= t-|{\bf{r}}-{\bf{r}}'|/c $ is the delayed time. Considering the radiated field in the far field zone, $ |{\bf{r}}-{\bf{r}}'|\approx r - {\bf{n}}\cdot{\bf{r}}' $, where $ {\bf{n}} $ is the unit vector in the emission direction, and performing the Fourier transform in time, we have then the following expression for the vector potential

where $ {\bf{j}}_\omega $ is the Fourier component of the current and $ k=\omega/c $ is the wave number of emission. Since the emission zone is smaller than the wavelength of emission, $ kz_0 \ll 1 $, we develop the exponent under the integral in Taylor series, $ {\rm{e}}^\xi=\sum\nolimits_j \xi^j/j! $, and the terms in this series correspond to multipole expansion.

The terms $ j=0 $ and $ j=1 $ do not contribute to the radiation because $ \int d{\bf{r}}'\, {\bf{j}}({\bf{r}}')=0 $ and also $ \int d{\bf{r}}'\, {\bf{j}}({\bf{r}}') \,{\bf{n}}\cdot{\bf{r}}'=0 $. The first relation is evident since the current is a derivative of magnetic field: $ {\text μ}_0 j_x=\partial_y B_s $ and $ {\text μ}_0 j_y=- \partial_x B_s $. The second relation is obtained by integrating by parts the left-hand side and knowing that the integral of the magnetic field over $ y $ is zero. Thus, a non-zero contribution comes from the quadrupole term $ j=2 $, which is written as:

where $ {\bf{z}} $ is the unit vector in the laser propagation direction, and $ B_\omega $ is the Fourier component of magnetic field $ B_s $. The integral over the magnetic field at the source can be performed using the analytic approximation for the magnetic field Eq. S.6. Taking then a curl of the vector potential, we have the magnetic field in the far field zone:

where $ b_\omega= t_{\rm{dif}}/(2+i\omega t_{\rm{dif}}) $ is the Fourier component of the time-dependent factor in Eq. S.6. The last factor accounts for the suppression of the emission because of a small ratio of the emission zone to the emission wavelength, $ kw_0 \ll 1 $.

Knowing the magnetic field in the far field, we calculate the electric field as $ {\bf{E}}=-c {\bf{n}}\times{\bf{B}} $ and obtain the emission power in the solid angle $ d\Omega $:

Integrating the emission power over time, we obtain the total emitted energy. Using the theorem of Parceval, $ \int f^2(t)\,dt= (2{\text π})^{-1} \int |f_\omega|^2d\omega $ we replace the integral over time with the integral over frequency and obtain the spectrum of emission:

In the spherical coordinate system with the polar axis along the z direction and azimuthal angle $ \varphi $ in the $ (x,y) $ plane with respect to the $ x $ axis, we have $ n_{\textit z}=\cos\theta $ and $ n_y=\sin\theta \sin\varphi $, so the angular dependence of the emission power is

Since both electric and magnetic fields are proportional to $ n_y $, the maximum of emission is in the $ y $ direction. The polarisation is in the $ {\bf{n}}\times{\bf{z}} $ direction; that is, the polarisation is perpendicular to the observation direction in the plane defined by the observation direction and the $ x $ axis. The function under the integral represents the emission spectrum:

Divergence of the spectrum at high frequencies is due to the discontinuity in the time dependence of the magnetic field $ B_s $ at time $ t=0 $ corresponding to the shock ionisation by laser and electron heating. There are several options to introduce the switch-on time of the magnetic field generation: the laser pulse duration, the electron collision time, and the time of laser pulse propagation along the focal volume. Among the three options listed above, the longest one is the latter: $ {\textit z}_R/c\simeq 0.2 $ ps. Since $ ct_{\rm{dif}}\gg {\textit z}_R $ the integral over the spectrum is dominated by the cut-off frequency $ \omega_{\rm{cut}}\simeq c/{\textit z}_R $, corresponding to the cut-off wavelength of $ 60\,{\text μ} $m and frequency of 5 THz.

Integrating the emission power over the angles and spectrum, we obtain the total emitted energy:

Comparing the radiated energy $ W_{\rm{rad}} $ with the energy stored in the magnetic field in the focal zone, $ W_B=B_{\max}^2 V_{\rm{las}}/2{\text μ}_0 $, the factor $ (w_0/{\textit z}_R)^4= ({\rm{NA}}/0.61{\text π})^4=1.8\times 10^{-5} $ defines the emission efficiency. For the magnetic field energy of $ 6.6\,{\text μ} $J, the radiated energy is 81 pJ, and the radiation power is about 400 W. That estimation is about four times larger than the measured emitted energy of 22 pJ, which can be considered as a reasonable agreement.

The theoretical estimates for the frequency cut-off and the emitted energy are compatible with the observations. The analytical expressions for these parameters show the way of further improvements. The conversion efficiency of the magnetic field into radiation can be increased either by increasing the ratio $ w_0/{\textit z}_R $ with a tighter laser beam focusing or by creating a non-zero average magnetic field in the plasma. This will increase the conversion efficiency by a factor of $ ({\textit z}_R/w_0)^2 \sim 100 $. The structure of the magnetic field given by Eq. S.6 corresponds to the circular laser beam interacting with a planar shock. To produce a non-zero average magnetic field one may consider an elliptic laser beam with the ellipse axis at an angle (not equal to 0 or 90°) with respect to the $ x $ axis.

Another possibility of increasing emission consists of increasing the magnetic field energy. According to the analysis of Eq. 8, the generated magnetic field depends effectively on two plasma parameters: electron temperature $ T_e $ and shock front width $ d_{\rm{sh}} $. The magnetic field energy depends on electron temperature with the fifth power. So, even a modest increase in electron temperature by a factor of 1.5 will increase the emission energy by 10 times. This can be achieved by increasing the energy of the main laser pulse.

In conclusion, the theoretical analysis of THz emission in air with two laser pulses confirms the hypothesis proposed by Huang et al.²⁷ that the emission is produced from a plasma created by the main pulse in the shock front. The theoretical estimates of the plasma and shock parameters are in agreement with the measurements. However, the mechanism of electromagnetic emission is different from the diffusion current in semiconductors³⁸. An electrostatic current related to the charge separation cannot be excited in plasma. Instead, a rotation current is created by non-parallel gradients of electron density and temperature. This current induces a magnetic field and produces a magneto-quadrupole electromagnetic emission. The emission wavelength is controlled by the length of the laser focal region and can be varied by changing the numerical aperture.

By using two pre-pulses with the same timing at focal spots placed at different 3D locations with respect to the focus of the main pulse, it is possible to engineer air density gradients arriving at the main irradiation site. An addition of two perpendicular air density gradients $ \nabla_y\rho $ and $ \nabla_x\rho $ allows one to control the ellipticity and intensity of the emitted THz radiation. A single cycle circular polarisation THz radiation can be produced. By placing $ d\sim 10\; {\text μ} $m-diameter focal spots in 3D space with separations of $ (3-5)\, d $ in space and $ \sim 10 $ ns in time, it is possible to synchronise the arrival of shock wave fronts travelling at high Mach $ (3-10)\; {\text μ} $m/ns speeds in the air for THz emission enhancement and polarisation control at the laser pulse intensities of a fully deterministic tunnelling ionisation $ 10^{16} $ W/cm².

The origin of THz emission is the current induced at the crossed plasma density and temperature gradients, called the Biermann battery effect ⁴⁰. This study clarified that the electrostatic current related to the charge separation cannot be excited in plasma. A coalescence of two shocks at the position of the main pulse produces stronger air compression than a single pulse, thus generating a stronger THz emission at a shorter wavelength. Since the electron current is proportional to the electron temperature and inversely proportional to the shock thickness, the way to increase the power of THz emission would be the increase of electron temperature and the strength of the shock.

After the collision of two shocks created by two pre-pulses, the interaction of the main laser pulse with the compressed air creates a plasma with asymmetric density distribution, which affects the intensity and polarisation of the THz emission in a two-fold way. First, the three-dimensional density asymmetry produces the anisotropy of pressure force and permits the current circulation on a picosecond time scale. Second, the shock density gradient is defined by the angle of collision of two shocks created by two pre-pulses. It is not necessarily aligned along the line connecting the pre-pulse and the main pulse, which affects the polarisation of the THz signal. The privileged direction of THz emission is in the plane perpendicular to the laser pulse propagation. This is the theoretical prediction that is verified in the experiment.

An example of a high-density micro-target for the generation of an extreme UV emission at 13.5 nm for the next generation of photolithography is realised by irradiation of 20-μm diameter Sn micro-spheres by a focused 10 μm wavelength CO₂ laser⁴¹. Similarly, micro-jets of Ga produced by laser pulse showed a strong enhancement of X-ray generation⁴². In water, micro-droplets and micro-sized gradients of compressed air serve the same purpose of delivering more material into laser pulse/beam, which results in plasma with higher density and temperature^{43, 44}.

All the experiments were conducted in air under atmospheric pressure (1 bar) at room temperature (RT; 296 K). The experimental setup is described in detail elsewhere³⁰. A pulsed femtosecond laser (35 fs, transform-limited, $ \lambda = 800 $ nm, 1 kHz, Mantis, Legend Elite HE USP, Coherent, Inc.) was used and the output pulses were split into the main pulse (linearly-polarised parallel to the $ x $-axis, $ x $-pol., 0.4 mJ) and the pre-pulse, then the pre-pulse was further split into a pre-pulse 1 (linearly-polarised parallel to the $ y $-axis, $ y $-pol., 0.2 mJ) and a pre-pulse 2 (linearly-polarised parallel to the $ y $-axis, $ y $-pol., 0.2 mJ). THz emission is induced by tightly focusing the main pulse with an off-axis parabolic mirror (1-inch diameter, focal length $ f = 50.8 $ mm, 47-098, Edmund Optics) into air with a time-delay, $ \Delta t = 9.7 $ ns, between the main pulse and both of the pre-pulses arrival. Under the main pulse focusing condition with effective numerical aperture $ NA= 0.125 $, the laser focus area was estimated to be about $ 8\; {\text μ} $m in diameter and $ 120\; {\text μ} $m in length along the axial direction (depth-of-focus)³⁰.

Splitting and spatial offsets of the two pre-pulses along the $ x $- and $ y $-axes, $ \Delta x $ and $ \Delta y $, were made possible with a Liquid Crystal on Silicon-Spatial Light Modulator (LCOS-SLM, X15213, Hamamatsu Photonics). The homemade program used computer-generated holograms (CGHs) that form multiple focal points and display them on the LCOS-SLM. CGHs were optimised by the weighted Gerchberg-Saxton (WGS) algorithm⁴⁵ for the uniform intensity of the focal points. The pre-pulse 1 was set stationary at ($ \Delta x_1 $, $ \Delta y_1 $, $ \Delta {\textit z}_1 $) = ($ 0\; {\text μ} $m, $ +33\; {\text μ} $m, $ 0\; {\text μ} $m) while the pre-pulse 2 was scanned in three dimensions along the $ x $-, $ y $-, or z-axis using 3D holographic focusing⁴⁶.

The detection of the THz wave emission is achieved by the standard electro-optic sampling method (see Appendix “Electro-optical sampling”), THz time-domain spectroscopy (THz-TDS), in the transmission direction along the z-axis with a $ \langle 110\rangle $-oriented ZnTe crystal (1-mm thick, Nippon Mining & Metals Co., Ltd.)^{9, 30, 47}. The measurements of the THz polarisation were carried out with a set of wire grids before the detection $ \langle 110\rangle $-oriented ZnTe crystal following the standard procedure⁴⁸⁻⁵⁰. Both polarisations of the THz emission $ (E_x,E_y) $ were determined from the event of laser irradiation by the main pulse via calculation of the measured fields $ E_{\pm 45^\circ} $ using $ \pm45^\circ $ orientated wire-grid polarisers in respect to the $ x $-polariser (high transmission) placed just before the ±45° polariser. The effective repetition of the laser excitation is at 0.5 kHz to restore the same air conditions for subsequent laser shots. Two laser pulses (main) were required to determine $ E_{-45} $ and $ E_{+45} $ components separately. Transient of THz emission was established from separate laser shots for the −5 to 15 ps $ (E_x,E_y) $-projections.

This research was funded by the National Science and Technology Council (NSTC, formerly known as MOST) of Taiwan 107-2112-M-001-014-MY3,110-2112-M-001-054 (K.H. and H-H. H.) and partly funded by the Australian Research Council Linkage LP 220100153 grant (S.J.). We are grateful to Prof. Eugene G. Gamaly for the critical comments.