-
Photon, with its characteristics of long coherence time, ease of manipulation, high-speed operation, suitability for long-distance transmission, and tolerance for a wide range of operating temperatures, is considered an ideal carrier for quantum information processing1–3. As a result, pioneering work in fields such as quantum nonlocality verification4, quantum teleportation5, quantum communication6, and quantum computing7 have largely been achieved using photonic systems. After decades of development, photonic-based quantum communication systems have expanded to satellite-ground scales8,9, and metropolitan-area quantum communication networks have been established10,11, indicating that quantum communication is gradually entering the practical stage. Photon entanglement has also progressed from initial two-photon, two-dimensional entanglement12,13 to multi-photon, high-dimensional entanglement, providing a robust platform for quantum information processing14–17. Notably, in quantum computing, the Jiuzhang experimental platform based on multi-photon systems demonstrates that quantum advantage can be achieved using photonic systems18. However, compared to other solid-state systems, photonic-based quantum information processing platforms are often relatively large. Although advancements in photonics integration continue, realizing large-scale photonic quantum computing devices still faces technical challenges. Therefore, achieving integration and miniaturization of the photonic platform has become imperative.
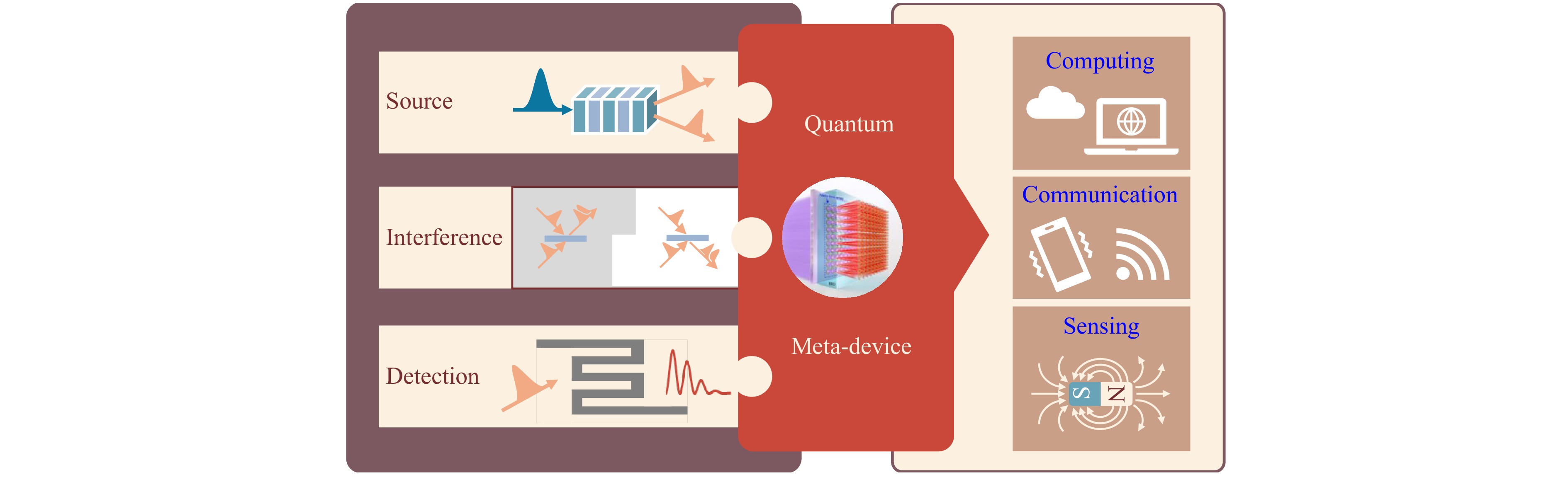
In recent years, there has also been a growing interest in replacing bulky optical elements with ultrathin meta-replicas19–21. Thanks to the capability of flexible control over multiple degrees of freedom of light at subwavelength scales, a single metasurface optical device can often integrate multiple functions traditionally performed by separate optical components. Additionally, due to compatibility with CMOS fabrication processes, metasurfaces can be integrated with other photonic integrated platforms22–24. Thus, optical metasurfaces have become a promising candidate for building miniaturized quantum information processing platforms. On the other hand, some counterintuitive light-matter interactions at subwavelength scales can also provide unexpected functionalities for quantum information processing25. Metasurfaces can solve important problems in quantum optics platforms in the following three aspects3: First, scalable multi-photon sources, which are essential for demonstrating quantum advantages, necessitating reliable generation of non-classical states including single photons and entangled pairs; Second, controllable large-scale interference network devices which are crucial for quantum information processing, extending beyond traditional beam splitter functionality to enable manipulation of multiple degrees of freedom, including orbital and spin angular momentum states; Third, high-efficiency detection systems capable of single-photon-level sensitivity with minimal recovery time. These detectors must achieve near-unity detection efficiency to capture photons, which is crucial for quantum state reconstruction and information recovery.
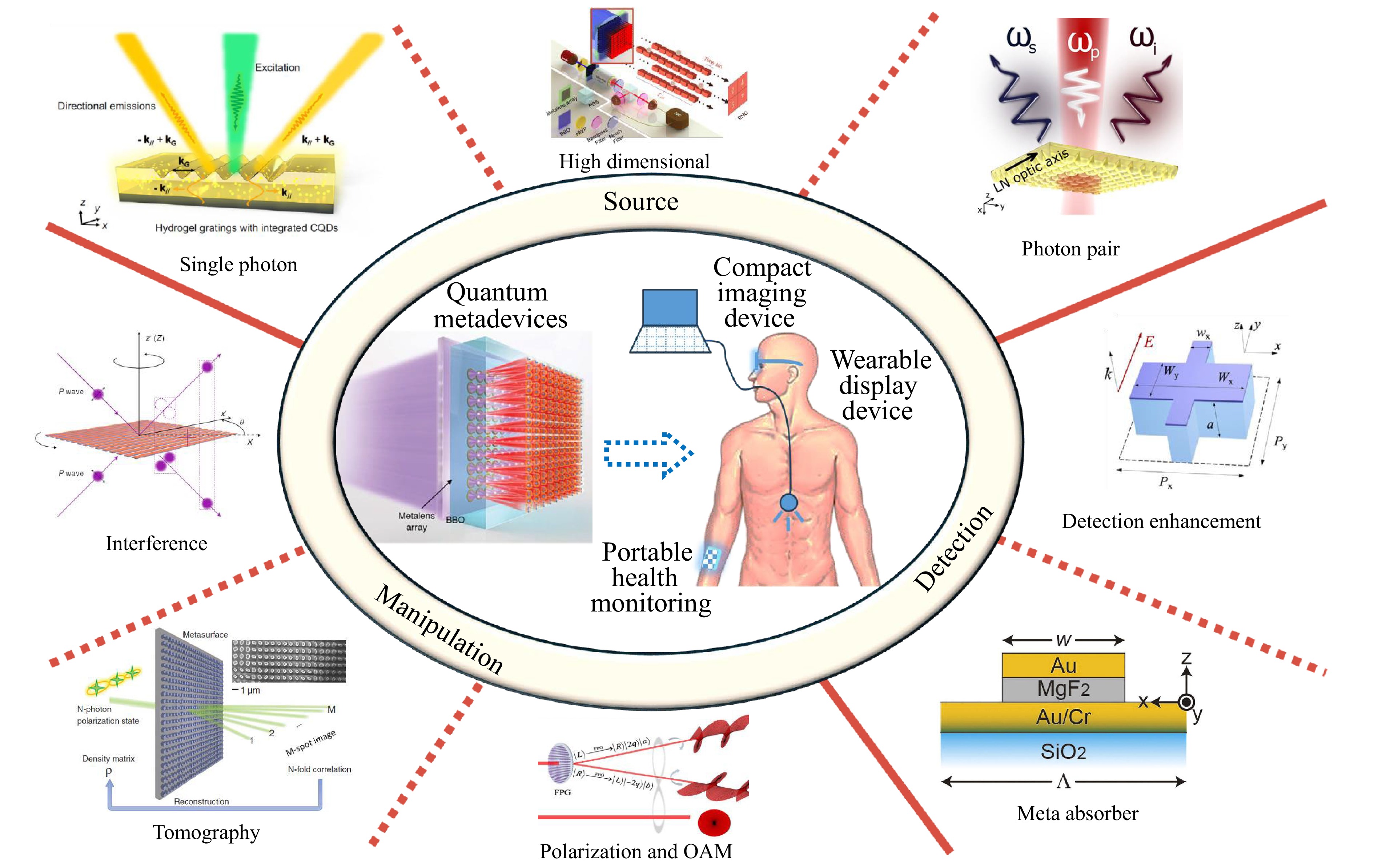
In this review, we provide a detailed analysis of the convergence between metasurfaces, meta-devices, and quantum photonics, highlighting how these innovative fields are advancing quantum optical technologies. We begin by exploring the evolution and significance of quantum technologies in contemporary photonics, and we assess how the inherent capabilities of metasurfaces and meta-devices contribute to the advancement of quantum development. Next, we present illustrative case studies that showcase examples of metasurfaces and meta-devices in quantum systems, demonstrating the straightforward implementation of typical quantum experiments using metasurface platforms. Finally, we share our insights and perspectives on the future development of quantum meta-devices. Fig.1 presents the overall structure of this review and outlines the main topics discussed.
-
Recent advances in nanofabrication techniques have enabled the development of metasurfaces. These two-dimensional (2D) planar artificial electromagnetic structures are composed of subwavelength-sized metallic26, dielectric20, and their hybrid resonators. The reduced dimensionality of metasurfaces, compared to their three-dimensional metamaterial counterparts, offers significant advantages, including enhanced integration density and simplified fabrication processes, while maintaining efficient control over multiple independent optical degrees of freedom, including wavelength, polarization, amplitude, and phase.
Metasurfaces exhibit distinct resonant behavior through their subwavelength scales than traditional diffractive flat optics, enabling selective mode control for specific optical functionalities. These subwavelength structures support different operation modes: phase manipulation of free space propagating modes27–29, and local/non-local resonances and their hybrid modes that facilitate in-plane structural interactions. The local modes encompass Integrated-resonant unit21,30, Mie scattering31, and Moiré flat bands32, while non-local modes manifest as periodic lattice resonances described through Bloch theory33. Hybrid modes show superiority in specific functions, such as enhancement of field34,35 and efficiency36. The most representative application is achromatic Metalens37,38. This sophisticated interplay between different modes of behaviors makes metasurfaces particularly versatile for precise manipulation of electromagnetic fields, offering a powerful platform for controlling light-matter interactions at the subwavelength scale and introducing unprecedented control dimensions for quantum technology.
The exploration of quantum applications of meta-devices initially centered on plasmonic platforms, leveraging their unique bosonic nature39. Despite their potential for seamless integration with electronic circuits through electron-photon hybridization, plasmonic face fundamental challenges in achieving quantum advantages at macro scale. The inherent trade-off between loss and mode confinement presents a critical bottleneck: low-loss plasmonic modes require larger mode volumes, while highly confined modes suffer from substantial losses40, thereby limiting both scalability and quantum coherence. This dilemma prompted a paradigm shift towards dielectric platforms, which demonstrated breakthrough scalability in quantum network devices on on-chip Silicon photonics. The success of dielectric-based quantum meta devices, particularly exemplified by the work on large-scale integrated quantum networks41, has catalyzed rapid advancement in dielectric quantum photonic technologies.
The subwavelength structures of metasurface enable precise manipulation of multiple degrees of freedom, including wavelength positioning of quantum sources17,42, polarization dimensionality43, emission intensity44, and phase control45,46. All of them are crucial for quantum state engineering. Through manipulation behavior in various eigenmodes, metasurfaces can deterministically enhance both emission and detection efficiencies. Their inherent subwavelength architecture facilitates miniaturization and integration, making them particularly attractive for scalable quantum technologies.
The upcoming sections will address several key aspects: an examination of the differences between quantum and classical light, an exploration of the mechanics behind quantum light sources and quantum interference, and a highlight of important quantum applications enabled by meta-devices. As depicted in Fig. 2, The discussion will begin with an introduction to quantum light sources, including photon pair generation by spontaneous parametric down-conversion (SPDC), single-photon generation and high dimensional entangled photons generation. This will be followed by an in-depth look at quantum interference and photon manipulation. Finally, the critical role of entangled photons will be illustrated through key application areas such as quantum imaging, quantum metrology, quantum communication, and quantum computing.
-
Quantum light is a state of light that has no classical equivalent. Early research of quantum light involves investigations on single photons, squeezed states, twin beams and Einstein-Podolsky-Rosen states47. With the development of quantum optics, the research of quantum light turned into more complex systems involving many modes of spatial, temporal, frequency, and polarization types. The quantum light source is the source that is able to generate quantum light, which includes single photon sources like Nitrogen-Vacancy (NV) color center and quantum dots, entangled photon sources, and squeezed light sources, which mainly rely on nonlinear crystals. In this review, SPDC entangled photon source and single photon source are introduced for their compatibility with optical metasurface.
SPDC is an optical nonlinear process that was initially described as the "decay" of a high-frequency photon, which generates two low-frequency photons through a high-frequency photon48. The SPDC process is typically employed to generate pairs of photons. However, under specialized conditions, such as within superconducting cavities, this process can be extended to facilitate the production of triplet photon states49. The scope of our discussion is confined to the phenomenon of photon pair production. Photons generated through SPDC must comply with the principles of energy (left panel of Fig. 3a) and momentum (right panel of Fig. 3a) conservation. Consequently, the relationships among the frequencies and wave vectors of the pump photon, the signal photon, and the idler photon, which refers to the other photon besides the signal photon in the biphoton generation process, are subject to specific constraints50,51.
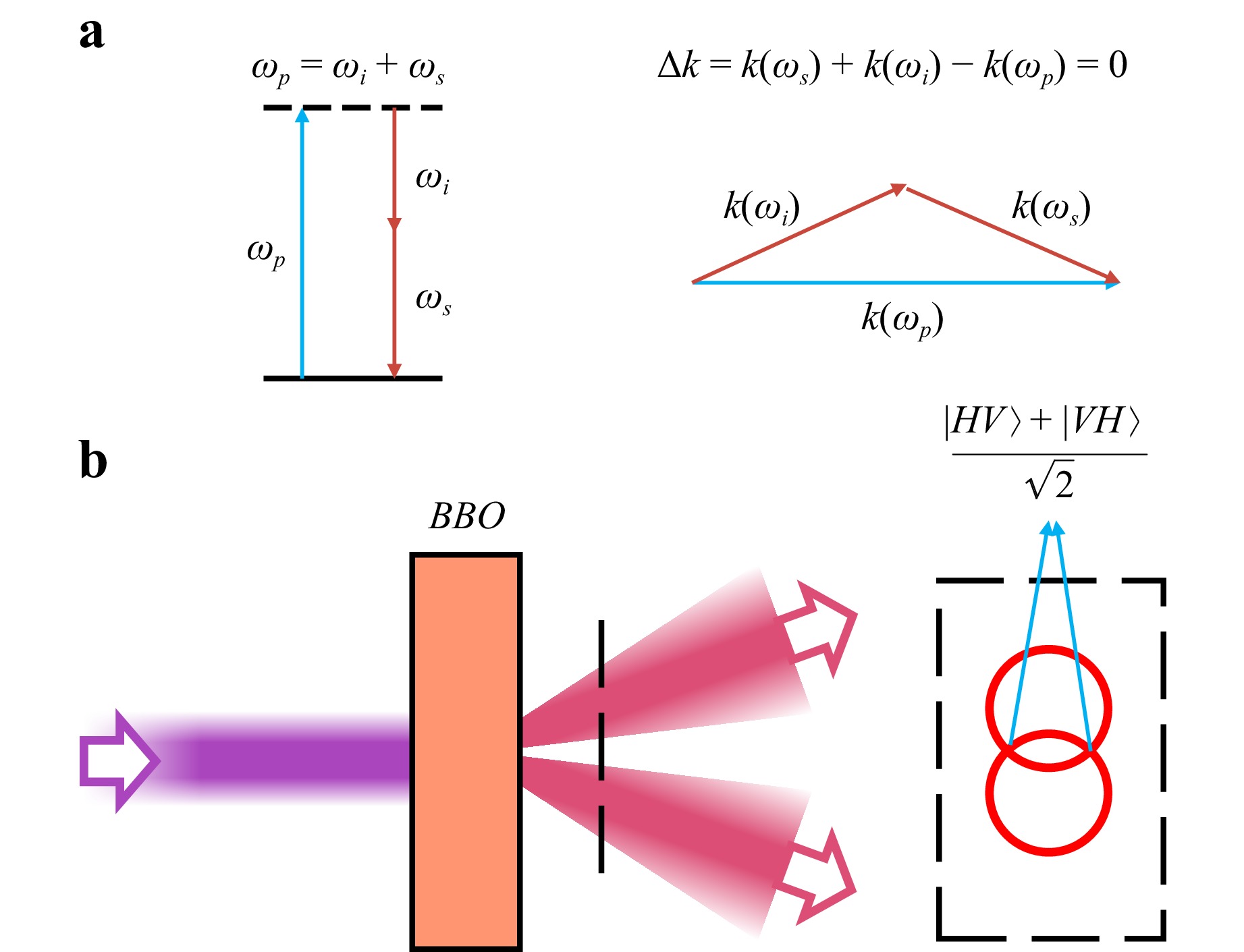
Fig. 3 Schematic drawing of SPDC process. a Energy and momentum conservation in SPDC process. A pump light photon (blue) splits into two down-converted photons (red). The entire process needs to comply with the conservation of photon energy (frequency) and momentum. b Generation of polarization-entangled photons by a Type-II BBO crystal. At the intersection of the two illuminated regions, two polarization modes converge, thereby obscuring the ability to ascertain the specific polarization mode to which a given photon corresponds. This phenomenon leads to the establishment of polarization entanglement.
In many cases, the frequencies of the signal and idler photons are the same, which is beneficial for two-photon interference. However, in some instances, the frequencies of the signal and idler photons can differ significantly, leading to various applications related to quantum imaging. In practical applications, the inherent dispersion of the nonlinear crystal contributes to a non-zero phase mismatch, resulting in destructive interference after a certain propagation distance $\delta_c=2{\text π}/\Delta k $. This phenomenon ultimately leads to a decrease in nonlinear efficiency.
A common solution to this issue is to compensate for the phase mismatch by utilizing the birefringent properties of the material, a method known as quasi-phase matching52. This approach helps achieve a longer coherence length and improves nonlinear efficiency. Different crystals have different application scenarios. Here, we take a Type-II crystal as an example to explain the reason for the generation of entangled photons in the SPDC process, which is illustrated in Fig. 3b.
If a pump light with a Gaussian spatial profile is considered, it will be observed that the mode function of the two-photon state must be satisfied $\Phi(q_s, q_i)\ne \phi(q_s)\phi(q_i) $, indicating that the mode functions of the signal and idler photons are inseparable. In conjunction with the entanglement criterion for pure states involving a few subsystems53, which is defined as a smaller component of a larger quantum system, it can be concluded that the two-photon state generated by SPDC exhibits entanglement.
In addition, photon pairs generated through SPDC display spatial correlations that manifest as anti-correlation in their wave vectors and consistency in their generation location. When observing a photon pair in the near field, it is guaranteed that the photons originated from the same location, as dictated by the SPDC mechanism. Conversely, in the far field, one can be certain that the two photons will be detected at opposite locations, consistent with the principles of momentum conservation inherent in the SPDC process. It’s worth noting that higher-order nonlinear effects, such as four-wave mixing, can also yield entangled photon pairs. However, for the purposes of this discussion, we will concentrate exclusively on SPDC and its applications.
The three most important parameters of bulk SPDC sources include indistinguishability, collection efficiency, and brightness of the light source54. For collection efficiency, the metasurface-based SPDC source can improve coupling efficiency by controlling the spatial mode of the output light through special design; for the brightness of the light source, by controlling the quality factor of the resonance, the metasurface can confine the field more in the nonlinear crystal to achieve a higher SPDC light brightness. Traditional sources require bulky crystals, which complicate optical alignment and limit the photon generation rate. Given that the probability of the spontaneous emission process is directly related to the quantum state density in the vacuum field, resonant localized modes excited in nanostructures offer a way to boost the efficiency of the SPDC process42,44,55-63. These modes can stably exist, effectively increasing the density of states near the resonant frequency.
As shown in Fig. 4a, Tomás Santiago-Cruz et al56. designed a periodic structure of truncated pyramids on a lithium niobate (LN) thin film. This metasurface supports Mie-type electric resonance with strongly localized fields, where the resonant wavelength is close to twice the pump wavelength, enabling efficient generation of signal-idler photon pairs with frequency degeneracy. Compared to the unetched thin film, the SPDC generation rate was enhanced by two orders of magnitude. Additionally, by altering the detuning between the degenerate wavelength and the electric resonance wavelength, the spectral width of the SPDC process can be further adjusted.
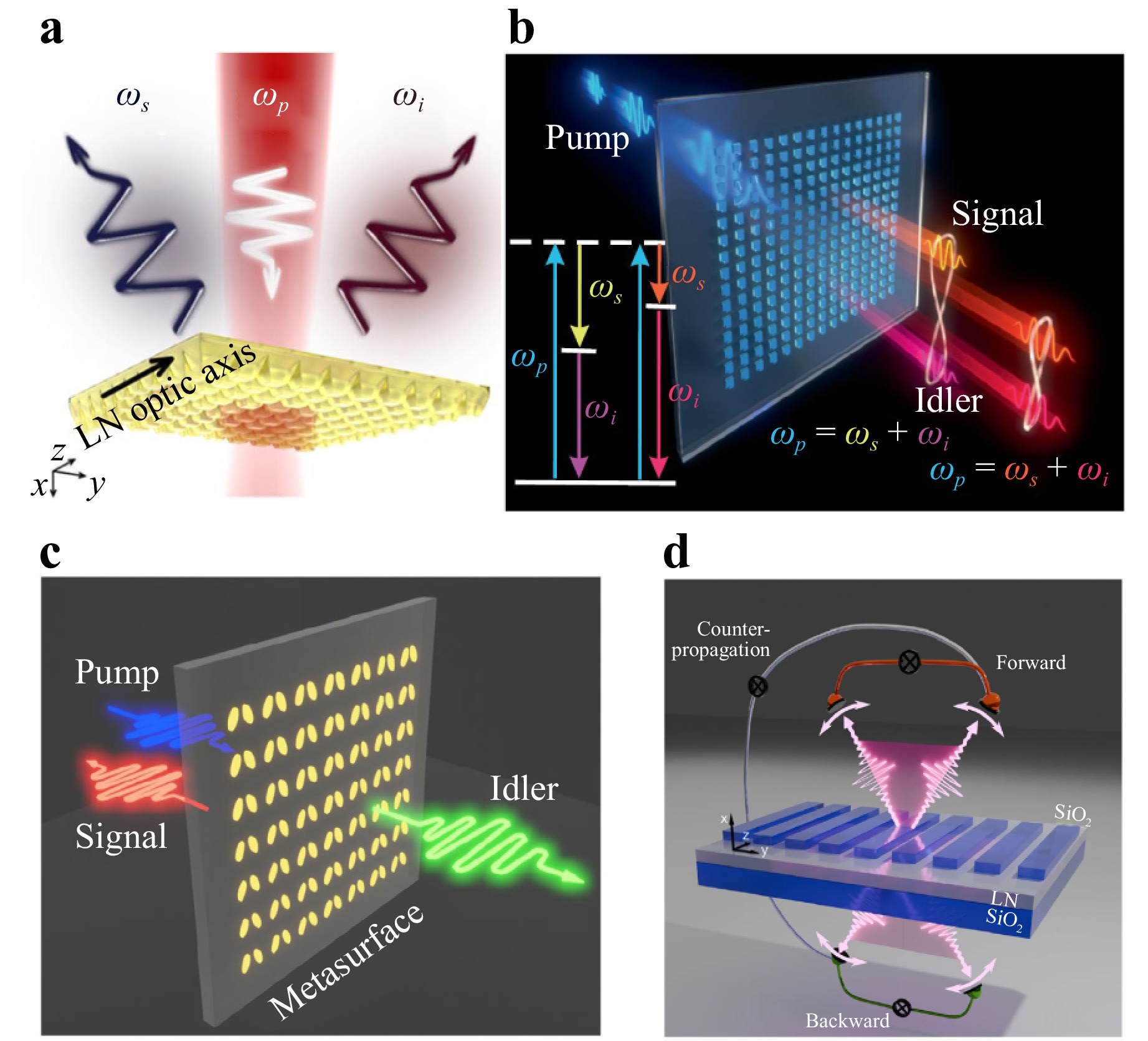
Fig. 4 Controllable SPDC Source Utilizing Resonant Metasurfaces. a Photon pair generation of Lithium Niobate film enhanced by resonances56. b Frequency control of photon pairs42. Metasurfaces are used to adjust momentum matching conditions. c Bidirectional photon pair emission59. Using metasurfaces to achieve SPDC photon reverse emission, which is not possible in general nonlinear crystals. d All-optical control of the photon pair emission angle61.
In general, according to the principle of energy conservation, multiple frequency combinations are possible for photon pairs generated from a given pump frequency. However, due to resonance, the probability of one particular frequency combination is significantly enhanced, corresponding to a resonant frequency and the difference between the pump and the resonant frequencies. This approach enables the generation of non-degenerate photon pairs, with specific frequency combinations accessible over a wide spectral range, by controlling both the pump and resonant frequencies. As shown in Fig. 4b, this concept was effectively demonstrated in the work of Tomás Santiago-Cruz et al42. They designed two types of metasurfaces: one supporting only electric resonance and another supporting both electric and magnetic resonances. Introducing the concept of bound states in the continuum (BICs)64 further enhances this framework. By reducing the net dipole moment of the nanostructures to approach zero, the coupling of resonant modes to free space is significantly weakened. This leads to a much higher Q factor, facilitating stronger electromagnetic field confinement and ultra-narrow emission spectra. Experiments revealed that in the SPDC process, photons consistent with the resonant frequency were observed in both metasurface designs.
The subwavelength thickness of metasurfaces confines photons to a limited thickness. As a result, the momentum uncertainty increases, thereby relaxing the longitudinal phase-matching requirements in nonlinear processes. Nevertheless, the SPDC still exhibits some degree of directionality. Therefore, investigating the directionality of photon pair emission is crucial. Building on the unidirectional scattering characteristics of metasurface resonant modes, Changjin Son et al.59 proposed a metasurface shown in Fig. 4c, where a quasi-BIC resonance is generated, manifested as an extremely narrow peak in the reflection spectrum. The signal photon of the photon pair is located within the resonance peak, exhibiting backward emission, while the idle photon outside the peak has an equal probability of being emitted forward or backward. It was measured that 56% of the photon pairs exhibited bidirectionality, enabling their path demultiplexing with a few nanometers of spectral detuning. Furthermore, a scheme for all-optical control of the photon pair emission angle was proposed by Maximilian A. Weissflog et al61. As illustrated in Fig. 4d, a nonlinear LN material forms a guiding layer, within which the degenerate photon pairs generated by the pump light excite two counterpropagating guided modes. The propagation constants of these modes are determined by the photon frequency, allowing for the adjustment of the photon’s transverse wavevector by varying the pump wavelength. The silica grating fabricated on the guiding layer provides additional transverse momentum, therefore enabling the photon pairs to couple into free space at different angles.
From the summary of SPDC enhanced by resonant metasurfaces in Table 1, it is evident that metasurfaces can effectively improve the performance of photon pair sources.
-
Single photons are another form of non-classical light existence, in addition to entangled photons65. Photon pairs generated through SPDC or four-wave mixing processes can create heralded single-photon sources with a wide range of applications. However, the probabilistic nature of nonlinear processes prevents them from becoming single-photon sources with high generation probabilities and high fidelity. The ideal single-photon source is a light source capable of generating a single photon in a specific mode upon demand. To approach this ideal, extensive research has been dedicated to isolated single-quantum systems that emit only one photon at a time. Current methods for generating single photons include capturing individual atoms or ions followed by optical excitation, harnessing electronic states in isolated molecules and defects in semiconductors, as well as utilizing optical transitions between quantum-confined states, isolated states, and electronic states in semiconductor quantum dots (QDs)66. Metasurface will be able to modulate the phase of the output light, thus approaching the single mode requirement of the on-demand single photon source.
Embedding a single-photon source within an optical cavity with resonant characteristics can substantially enhance the Purcell factor, thereby increasing the spontaneous emission rate67. To efficiently couple single-photon emissions, the surface plasmon polaritons (SPPs) mode is often employed68–75. For example, by placing a single photon source at the center of a spiral grating nanostructure on a metallic thin film, spin angular momentum69 and orbital angular momentum73 can be imposed on the emitted light by controlling the width or distance from the center of the nanoridges at various azimuthal angles. Meanwhile, the collimation of the radiation is ensured by the scattering properties of the spiral gratings.
Although metals have field localization capabilities that exceed the diffraction limit, their intrinsic losses also limit the use of plasmonic metasurfaces. In contrast, dielectric-based metasurface can avoid the loss problem. Therefore, hybrid plasmonic-dielectric metasurfaces76,77 and dielectric resonant metasurfaces78–83 have been explored to enhance single-photon emission by optimizing the interaction between quantum emitters and the local electromagnetic field. Resonances occur when a beam of light strikes nanostructures, causing induced polarization and displacement currents that generate electric dipoles (EDs) and magnetic dipoles (MDs), thereby amplifying the field intensity inside metasurfaces. To improve the coupling efficiency of photons emitted from quantum emitters (QEs) to the free space with arbitrary polarizations, the design by Samuel Prescott et al81. enables simultaneous excitation of both in-plane and out-of-plane EDs at the QE emission wavelength. This approach eliminates the alignment dependence of coupling enhancement for QEs without affecting their intrinsic emission rate. This design builds on their previous work, where they achieved an order of magnitude enhancement in emission intensity using Huygens' metasurface82, which refers to principles of generalized Huygens' wave theory in the design process.
However, the limited Q factor of Mie and Fano resonances imposes a significant constraint on their further development. As previously discussed, BICs facilitate high quantum efficiency. Luca Sortino et al83. integrated defect ensembles within hexagonal boron nitride and q-BIC resonances, achieving a 25 times enhancement in photoluminescence intensity and a narrowed spectrum with less than 4nm linewidth.
Table 2 summarizes the key characteristics of these resonance-enhanced single photon quantum sources.
References QEs Emission Wavelength resonance g(2)(0) Emission Modulation Collection Efficiency(%)/
Enhancement69 Nitrogen-Doped Nitrogen-Vacancy
(ND-NV)665 nm SPP 0.27 SAM 92% 73 ND-NV 670 nm SPP 0.22 SAM, OAM 97% 71 ND-NV 670 nm SPP 0.49 Radial Polarization 74% 82 GaAs QD 750 nm Mie 0.3 − 10 80 InAs QD 1200 nm Fano − − 110 83 hBN-VB− 760~900 nm q-BIC − − 25 Table 2. Resonance-enhanced single photon quantum source
Another remarkable feature of metal and dielectric metasurfaces is their capability to manipulate various parameters of light waves at ultrathin scales, introducing an abrupt interface in the propagation space to alter the spatial, phase, and polarization distributions of the light field. Among these, metalenses can effectively focus the emitted photons84, providing a solution for realizing directed radiation quantum light sources. For example, Tzu-Yung Huang et al.46 proposed a dielectric metalens on the diamond interface to collect photons emitted by the diamond NV centers located 20 μm below it, as demonstrated in Fig. 5a. Therefore, the quantum light source’s utilization efficiency and collimation are significantly enhanced. In the work above, the metalens only collect photons emitted from one side of the QE. If photons from the opposite side could also be collected, efficiency would be significantly improved. To achieve this, as shown in Fig. 5b, Yanjun Bao et al85. introduced a metallic mirror beneath the QD and precisely aligned the QD and its mirror image at the two foci of the upper-layer bifocal metalens. This arrangement allows both the photons emitted upwards and downwards to effectively interact with the nanostructures. Additionally, due to the extra optical path difference introduced when single photons propagate, the geometric phase modulation of left and right circular polarization (LCP and RCP) can be decoupled, enabling spatial separation of collimated photon beams with different spin angular momentum (SAM).
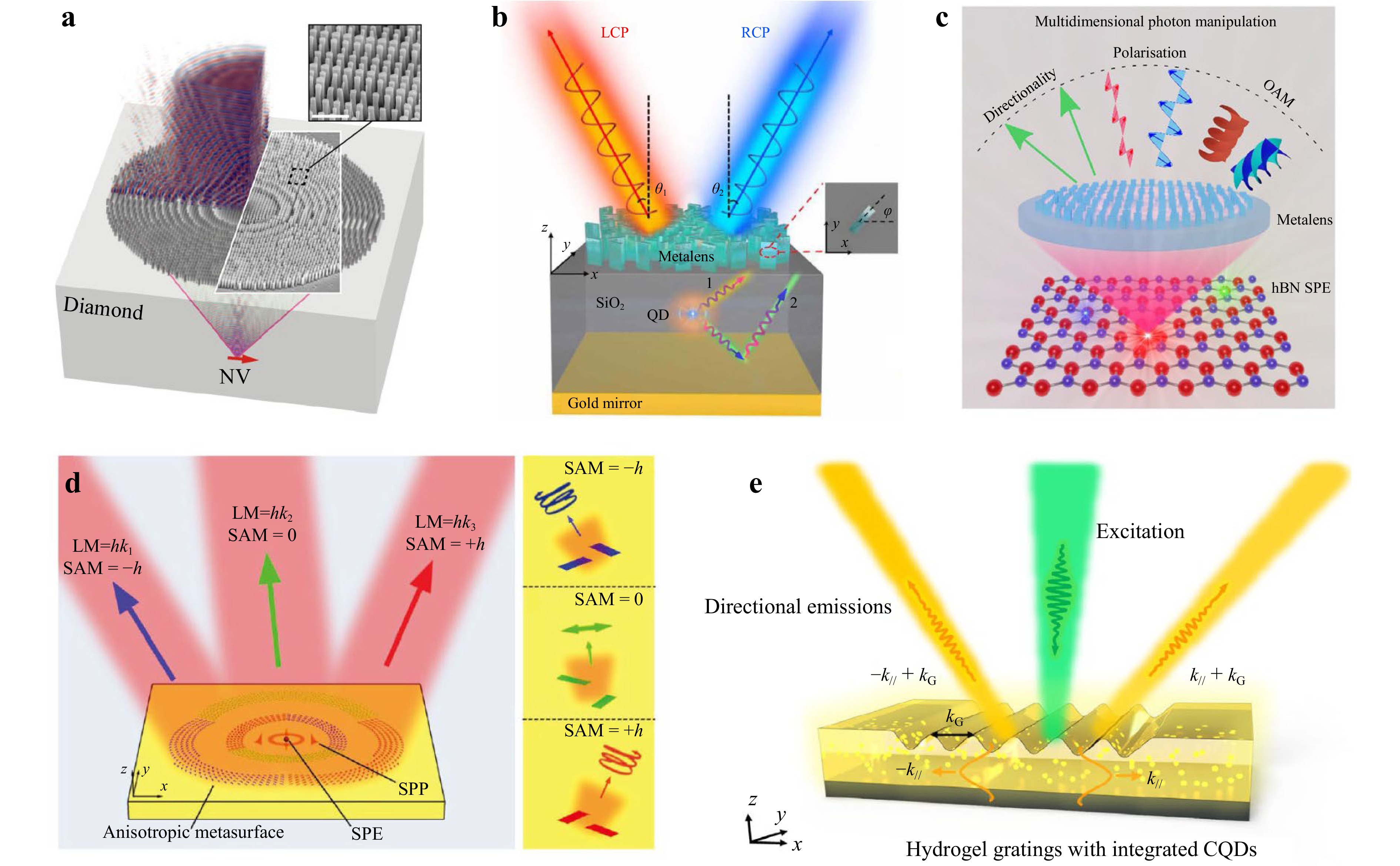
Fig. 5 Single-Photon Source Modulated by Metasurfaces. a Metalens collection and collimation of photons emitting from NV centers46. b Bidirectional photon emission collection and spin-separated beam generation by metalens85. c Metalens' simultaneous control of SAM and OAM86. This allows for directed complex single-photon emission with customized polarization and phase distributions. d Single photon linear momentum modulation97. e Tunable unidirectional single photon emissions based on hydrogel gratings98. The emission divergence angle was decreased to less than 1.5°.
Further leveraging the multifunctional integration advantages of metasurfaces, Chi Li et al86 combined 2D materials with metasurface, which have currently achieved multi-dimensional modulation of light waves including diffraction angle, polarization, and orbital angular momentum (OAM), on top of focusing and splitting functionality, as demonstrated in Fig. 5c. This enables complex single-photon emission directed towards specified directions with tailored polarization and phase distributions. What’s more, with the assistance of 2D materials87–89, more substantial optical nonlinear effects can be achieved in the hybrid structures of 2D materials and metasurfaces90,91. If the Spontaneous SPDC process is involved, it can be utilized to obtain enhanced entangled photon sources92–94. Besides, Xujing Liu et al95. also achieved independent and precise manipulation of single photon SAM-OAM states in an on-chip configuration. Furthermore, by incorporating the design principles of metasurface holography, the same group96 realized multichannel quantum emission with arbitrary SAM and OAM encoding. Momentum is also an important parameter of photons that can carry certain information, manifested as the emission direction. As mentioned in Ref. 85, the QE must be precisely positioned relative to the metasurface to achieve phase modulation without deviation from the designed values. As shown in Fig. 5d. To address this limitation and simplify operation, Shangtong Jia et al97. implemented both phase-independent and phase-dependent schemes to control the photon’s SAM and emission angle separately. In the experimental results, three directional emitting channels offering versatile combinations of polarization (linear, left circular, and right circular) and diffraction direction are enabled by arranging anisotropic nanostructures anisotropically to form a clover-shaped metasurface.
Structured by active materials, active metasurfaces can integrate various modulation functions within a single device in the time domain, enabling the selection of the desired operating mode through appropriate exciting conditions. As shown in Fig. 5e, to achieve active emission control, Chenjie Dai et al98. proposed a quantum dots-hydrogel integrated grating, whose morphology will change according to the alteration of the ambient humidity. the grating is fabricated from a thin film of mixed polyvinyl alcohol hydrogel and carbon quantum dots (CQD) by grayscale e-beam lithography. When adjusting the humidity from 40%-60% to 70%-90%, the grating efficiency will rapidly decrease by more than 7 times due to the swelling of hydrogel. The dynamic switch of unidirectional emission is also demonstrated by pumping the CQD on different sides of the grating. Compared with the real-time emission steering enabled by a spatial light modulator, the work expands the diffraction angle up to 45° and narrows the divergence angle to less than 1.5°, manifesting miniaturization and compactness advantages of metasurfaces.
-
A greater number of entangled photons can provide more functional channels, while higher entanglement dimensions offer greater control flexibility. However, as the number of photons increases, the difficulty of generating entangled photons also rises. Fig. 6a illustrates a solution that integrates an array of 10 × 10 metalenses with a 0.5-mm type II β-barium borate (BBO) crystal and greatly expands not only the number of entangled photons but also the entanglement dimensions, as proposed by Lin Li et al17. Each metalens in the array will create a focal point inside the BBO crystal under illumination and then emits a photon pair with a certain probability. When a photon pair is generated, a state of 100-dimensional path-encoded entanglement is established. The novel advantage of the metalens array lies in the controllable phase difference between each channel, e.g., the relative phase between different terms of the generated quantum state. The experimentally demonstrated two-dimensional, three-dimensional, and four-dimensional entangled states all maintained a fidelity above 0.9, as illustrated in Fig. 6b. Furthermore, the multiphoton source based on the same configuration is analyzed. High-performance four- and six-photon sources are characterized by 86.3% Hong-Ou-Mandel (HOM) interference visibility. Another advantage of the metasurface array lies in its ability to create a multiplicity of emission channels using only a single nonlinear crystal while generating the required quantum states at an exceptionally high spatial density (100 channels/mm2). To further explore the application potential of metalens-array-based quantum source, Yubin Fan et al99. proposed a high dimensional quantum random number generator. The working principle is as Fig. 6c. The randomness of each photon generation is ensured by the Poisson distribution of photon arrival times and the SPDC process. The random numbers are generated by recording the time bin in which a photon arrives and converting the corresponding time bin label into a binary value. Post-randomness extraction is not required in this process, and the generated random number sequence has passed the NIST randomness tests (Fig. 6d) and is resilient to attacks from a Generative Adversarial Network (GAN) .
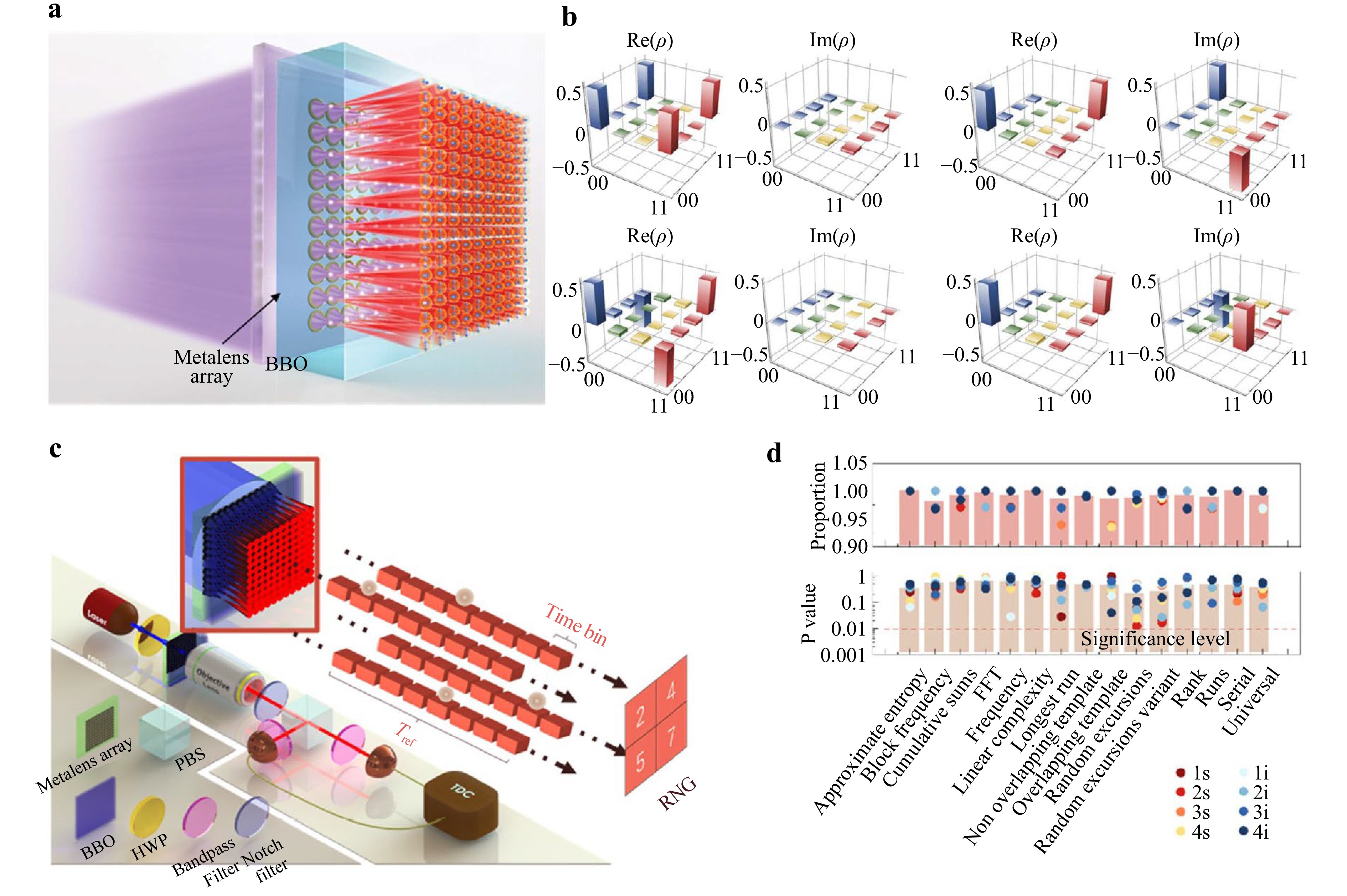
Fig. 6 High dimensional multiphoton quantum source with metalens array: a Metalens array enabled high dimensional and multiphoton source17. The challenge of generating high-dimensional entangled quantum states has been successfully addressed through the utilization of path entanglement. b Entangled quantum states generated by the metalens array represent fidelities larger than 0.9817. c Metalens array enabled high-dimensional quantum random number generator99. d NIST random test results99, which shows high randomness for the random numbers.
-
The primary distinction between quantum and classical systems lies in the many bodies under investigation and the intricate relationships between them. In the quantum realm, even the simplest interactions, such as those between two photons, introduce phenomena that are not addressed in classical physics. In 1987, researchers accomplished two-photon interference with identical photon pairs, which was later named as HOM effect, and the underlying principle is as follows100:
Initially, photon pairs are generated via a nonlinear process, with both photons reaching the beam splitter at the same time and possessing identical polarization. If we designate the two input ports of the beam splitter as a and b, and the output ports as c and d, the two-photon state can be expressed as follows:
$$ \hat a^{\dagger} \hat b^{\dagger}|0,0\rangle_{ab} \to \frac{1}{2}\Big(\hat c^{\dagger}\hat c^{\dagger}+\hat c^{\dagger}\hat d^{\dagger}-\hat d^{\dagger}\hat c^{\dagger} -\hat d^{\dagger}\hat d^{\dagger}\Big)|0,0\rangle_{cd}$$ (1) In the equation, $ \hat{a}^{\dagger} $ represents the creation of a photon from port a, and the negative sign in the formula originates from the phase shift due to reflection. Since the arrival times, polarization directions, and spatial modes of the two photons are identical, it is impossible to distinguish between the cases where the two photons exit through ports c and d separately. Therefore, the middle two terms in Eq. 1 can cancel each other out, leaving only the scenarios where the two photons exit through the two ports separately, which is the HOM effect (Fig. 7).
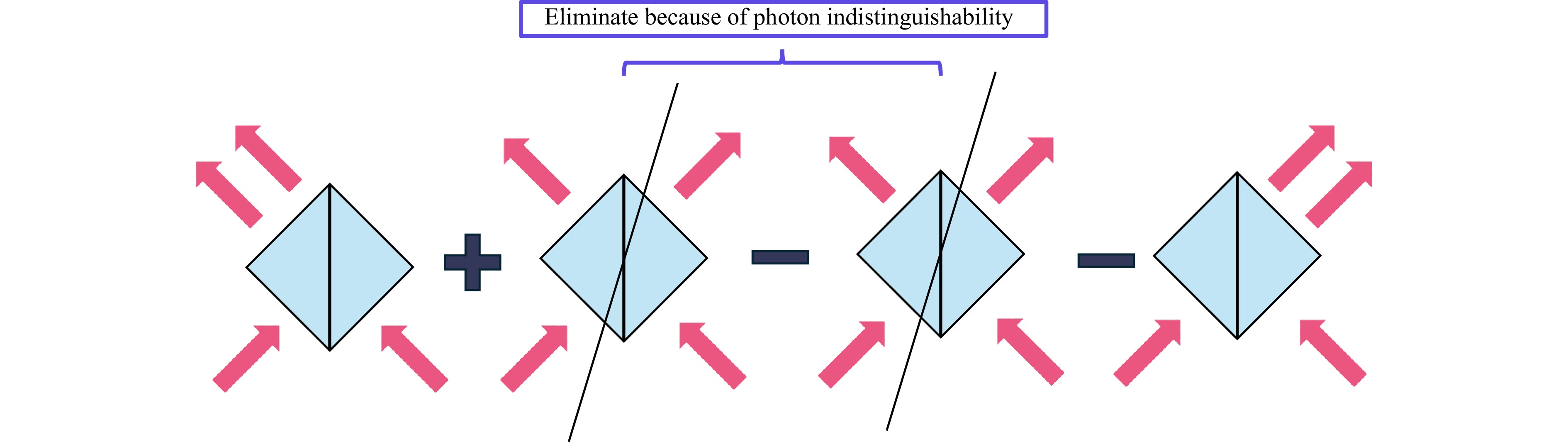
Fig. 7 Principle of HOM effect. After the photons from the two incident spatial modes interfere, the situation where one photon is assigned to each outgoing mode will cancel each other out, leaving only the situation where two photons are emitted from the same spatial mode.
The unique aspect of the HOM effect extends beyond the unusual behavior of photons; it is noteworthy for its capability to deterministically generate a specific quantum state known as the N00N state with N = 2, which means all of the two photons in the system goes to either output port of the beam splitter. When utilized in an interferometer, the N00N state can exceed the classical limits of uncertainty101. Moreover, the HOM effect has a wide range of applications, including measuring time shifts, enhancing high-precision Optical Coherence Tomography (OCT), conducting Bell state measurements, facilitating teleportation and entanglement swapping, enabling device-independent quantum key distribution, and supporting advancements in quantum computing. Notably, the HOM effect has also been observed in systems beyond photons, such as SPPs102 and electrons103.
Metasurface also offers significant advantages in shaping the entanglement properties, which is crucial in quantum communication, quantum sensing, and quantum computing. By tailoring the modulation properties of the metasurfaces, it is possible to generate photon pairs with specific polarization, frequency, and spatial correlations. One application involves inserting a metasurface with polarization-dependent selective transmission in the path of one photon in a polarization-entangled photon pair to enable entanglement distillation, as proposed by Motoki Asano et al104. Subsequently, Di Zhang et al105. extended this design to an all-optical manipulation framework.
The geometric phase arises from the interaction between a photon’s SAM and OAM. Leveraging this mechanism, Tomer Stav et al43. proposed a scheme in which a photon with linear polarization and zero OAM interacts with a metasurface carrying a helical phase, causing its left- and right-circular components to acquire opposite topological charges, thereby entangling SAM and OAM to form a single-photon entangled state, as illustrated in Fig. 8a. Additionally, they demonstrated entangled biphoton states, where the spin of one photon is correlated with the OAM of the other, with a metasurface conversion efficiency of 72%. Furthermore, Zhi-Xiang Li et al106. demonstrated a novel approach for encoding multiple degrees of freedom of the photons, including path, SAM, and OAM information into polarization-entangled photons using a dielectric metasurface designed as a fork-polarization grating (FPG). As depicted in Fig. 8b, when one of the two spin-entangled photons is sent through this metasurface and diffracted into two channels, it undergoes two key transformations: first, a spin conversion due to the geometric phase, and second, the imposition of OAM with topological charges of ± 1. This process can be represented as a four-qubit quantum state, which is promising for high-dimensional quantum information processing. To harness the potential of metasurfaces with multiple diffraction channels, Ya-Jun Gao et al107. employed the configuration shown in Fig. 8c, providing M and N distinct entanglement distribution and transformation schemes for the two entangled photons. This results in M × N possible photon pairs. Through optimization, the modulation of each diffraction order is made equivalent to that of a half-wave plate or quarter-wave plate, enabling the generation of various entangled states with both linear and circular polarization. For the input Bell state ψ+, three other Bell states and their superpositions can be achieved. Experiments confirmed the functionality of the design for 2 × 2 and 4 × 4 channel configurations. This work, realized with a very simple configuration, offers a promising path toward highly integrated solutions for quantum networking.
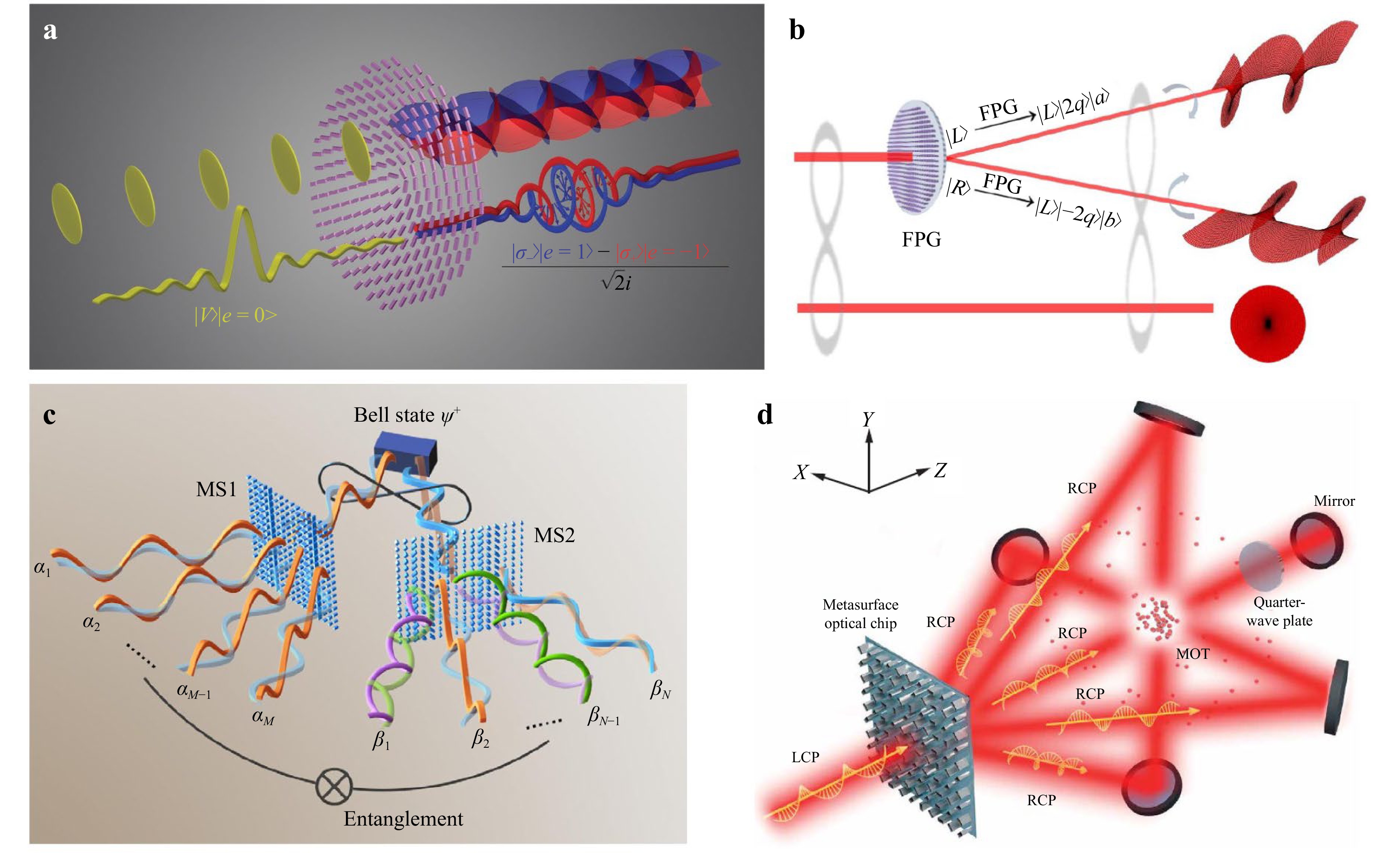
Fig. 8 Compact Light Modulation System Based on Metasurfaces: a Single photon SAM and OAM entanglement43. b Simultaneous encoding of path, SAM, and OAM of photon pair106. By controlling the polarization state of light in one path, a different spatial mode distribution can be obtained in the other path. c Multichannel two-photon entanglement generation107. d Metasurface magneto-optical trapping for cold atom generation108. Laser modulated by the metasurface can effectively reduce the speed of atoms in all directions, thereby achieving a cooling effect.
Metasurfaces present promising advancements in quantum state measurement technologies, offering the potential for system simplification and structural miniaturization and improving scalability and practicability. Apart from photons, cold atoms with precisely controllable quantum states are indispensable key components in quantum information, computing, and sensing systems. The magneto-optical trapping (MOT) is a commonly used method to obtain cold atoms, which requires three orthogonal pairs of circularly polarized counter-propagating laser beams. Lingxiao Zhu et al108. fully explored the ability of metasurfaces to manipulate the optical field with high degrees of freedom, making them a perfect counterpart for generating such directional beams. Fig. 8d demonstrates a metasurface working as a five-path fan-out element. Combining a mirror in each path, a MOT can be created. In the experimental verification, the number of trapped rubidium atoms approaches the theoretical limit of 107 while the temperature is about 35μK. Replacing traditional bulky optical components with metasurface to form a more compact cold atom source further drives the quantum systems towards miniaturization and integration.
Quantum interference serves as a key tool in applications including information processing and entanglement generation. Traditionally, bosons exhibit only bunching effects, while fermions only display anti-bunching effects. However, as shown in Fig. 9a, Quanwei Li et al25. designed a non-unitary metasurface to enable a continuous transition of P-polarization two-photon interference from bunching to antibunching by adjusting its rotation angle θ. In the metasurface design, no phase difference between the reflected and transmitted light when θ = 0, resulting in antibunching. Conversely, a π/2 phase difference is introduced when θ = π/2, resulting in bunching. These two conditions form a set of eigen-operations, and the coincidence detection probability for any value of θ between 0 and π/2 is a superposition of the probabilities corresponding to these eigen-operations. Additionally, this work also investigates the influence of independent polarization states of the two photons on the coincidence detection probability when the rotation angle θ is fixed at 0.
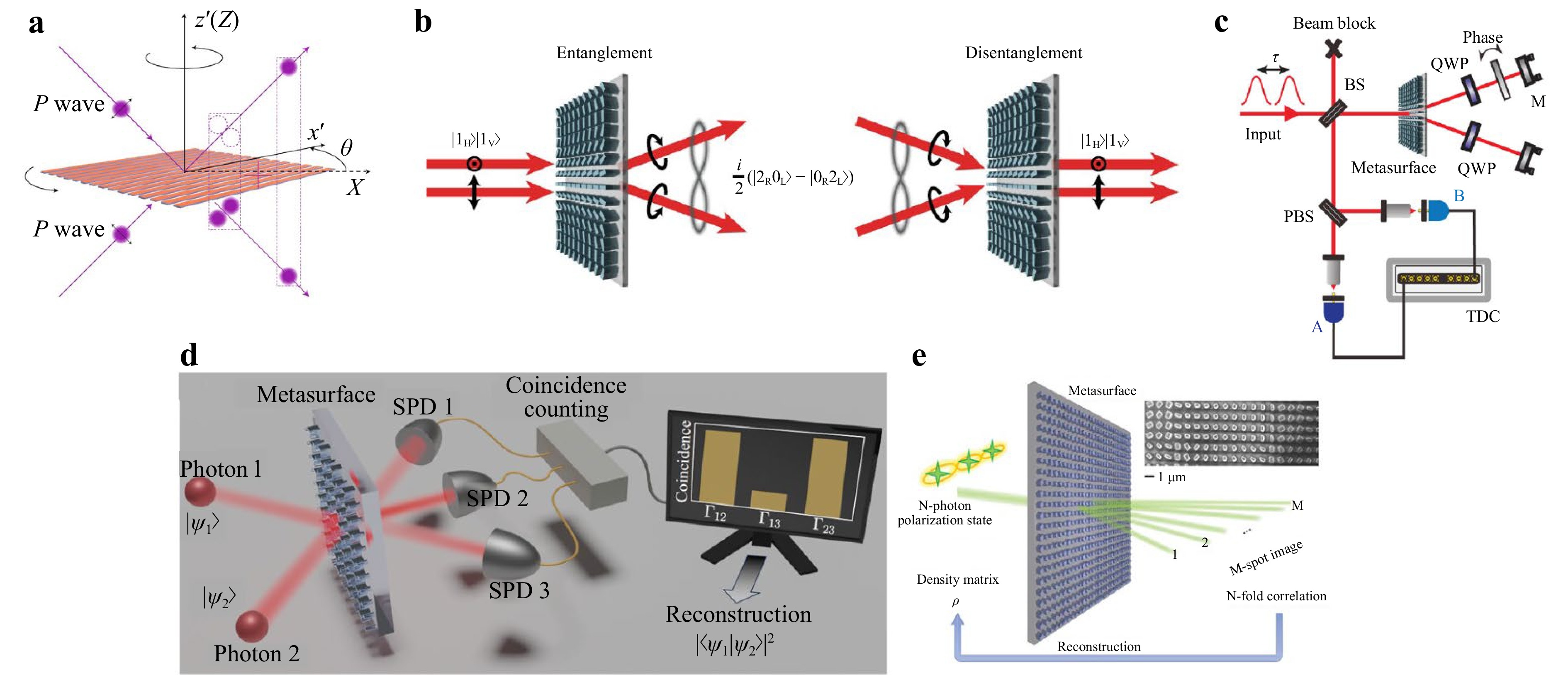
Fig. 9 Novel and Controllable Quantum Interference with Metasurface: a Generation of bunching, antibunching, and intermediate states of photon pairs25. Bunching or anti-bunching properties can be obtained at different incident angles by adding losses. b Generation of path entanglement and disentanglement109. Achieved polarization and path N00N state generation. c Phase measurement based on two-photon interference109. d Detection of photon indistinguishability110. e Multiphoton state reconstruction by polarization multiplexing metasurface112.
The bunching effect in two-photon interference can also be used to generate path entanglement and disentanglement. For example, Philip Georgi et al109. leverage a metasurface of geometric gradient phase, which can diffract LCP and RCP to two symmetric diffractions to the metasurface’s normal since their phase modulations have opposite signs. When the input states are $ {|1\rangle}_{H} $ and $ {|1\rangle}_{V} $, consisting of LCP and RCP components of equal possibility, they become indistinguishable by the metasurface, thus two photons will leave in the same diffraction path according to the HOM effect, which is demonstrated in Fig. 9b. Interestingly, the generated spatially entangled N00N state with nπ phase difference can be also disentangled by the same metasurface. The preservation of the quantum coherence of the generated entangled state is then verified by designing a folded metasurface-based interferometer shown in Fig. 9c. The coincidence between two output ports A and B oscillating with the phase difference $\varphi $ according to a function of $ cos2\left(\varphi \right) $, enabling an advanced quantum phase sensor with double period interference pattern.
The metasurface-enabled quantum interference can also be used to characterize the indistinguishability between photons. Jihua Zhang et al110. designed an interferometer, as shown in Fig. 9d, with two input ports and three output ports. By measuring the coincidences at the output and combining the transmission matrix of the metasurface, the two-photon indistinguishability can be deduced. This method effectively avoids the need for multiple delay-time measurements required in the HOM interference, as well as the multiple phase-delay measurements needed in Mach-Zehnder interferometry. With a single-shot characterization, it enables real-time evaluation of photon indistinguishability with a fidelity greater than 98.4%. Additionally, Zhanjie Gao et al111. proposed a complete measurement scheme for the four Bell states using a pair of binary metasurfaces.
With the ability to independently modulate multiple diffraction orders, metasurfaces provide an efficient platform for realizing multi-photon interference. By incorporating the propagation phase, the metasurface can further spatially separate elliptically polarized light with opposite handedness. Based on this Kai Wang et al112. elaborately selected M/2 elliptically polarization pairs that are as uniformly distributed as possible on the Poincaré sphere as basis vectors. Then their corresponding metasurface grating components are arranged in an interleaved pattern, as shown in Fig. 9e, which projects the input N-photon polarization state to the M channels. By measuring the N-photon correlations from the output beams, the density matrix can be effectively reconstructed. Compared to traditional quantum tomography, this work proposed a novel method to significantly decrease the number of required measurements from 4N to N + 3 for N photons. Later, the same group further bypassed the interleave arrangement design, using only a single metagrating with multiple output ports to achieve N-photon entanglement state measurement113. Each diffraction order acted solely as a near-perfect polarization splitter, thereby improving both compactness and detection efficiency.
-
Metasurfaces-based photodetectors, with their ability to control light at subwavelength scales, enhance light-matter interactions, enabling higher detection efficiency, faster response times, and higher functional integration. For example, Mark W. Knight et al114. fabricated metal nanoantennas on a semiconductor surface to form a Schottky barrier at their interface, effectively integrating the enhanced light coupling capability of the plasmonic resonances with the photoelectric conversion capability into a single miniaturized device. In meta-assisted quantum systems, single-photon detection still relies on traditional detectors. An important research direction is to fully exploit the unique resonant and absorption properties of metasurfaces to develop detectors with enhanced sensitivity and reduced detection loss. Atsushi Ishikawa et al115. achieved three major absorption peaks with 100% efficiency in the 30-150 THz range. This high absorption is realized by an Au/MgF2/Au trilayer structure depicted in Fig. 10a, where localized plasmons in the upper Au ribbon hybridize with their mirror images in the thick Au film to form asymmetric modes. Destructive interference between incident and re-radiated light, caused by out-of-phase charge oscillation, effectively cancels reflection and enhances absorption. Thomas Roger, et al116. experimentally demonstrated coherent perfect absorption at the single-photon level based on metamaterials. Fig. 10b demonstrates the designed perforated thin gold film with a 50% absorption rate for traveling waves. When a photon is split by a 50:50 beam splitter and enters the metasurface from both sides, it forms a coherent superposition state. When the phase difference between the two input channels is π, destructive interference occurs, resulting in 100% absorption. At this point, the photons couple into the localized plasmon modes of the metamaterial with nearly unit probability. The group further reported a scheme for the absorption of a two-photon N00N state with 40% efficiency117, which has the potential to advance applications in fields that rely on multiphoton upconversion but are limited by high peak intensities. As shown in Fig. 10c, Oleg Mitrofanov et al118. utilized subwavelength-sized interconnecting channels to solve the challenge of achieving electromagnetic dipole mode degeneracy and critical coupling for perfect absorption while maintaining electrical conductivity. The designed GaAs metasurface structure can provide perfect absorption for a desired wavelength in the range of 715 nm to 840 nm by simply adjusting the size of the interconnecting channels. This metasurface offers potential for applications in devices such as photoconductive switches and PIN photodiodes, enhancing their performance. Metasurfaces offer considerable potential in photon detection applications. By integrating metasurface absorbers, the coupling of light to photodetectors can be significantly enhanced. The improved efficiency can further accelerate advancements in the field of quantum optics.
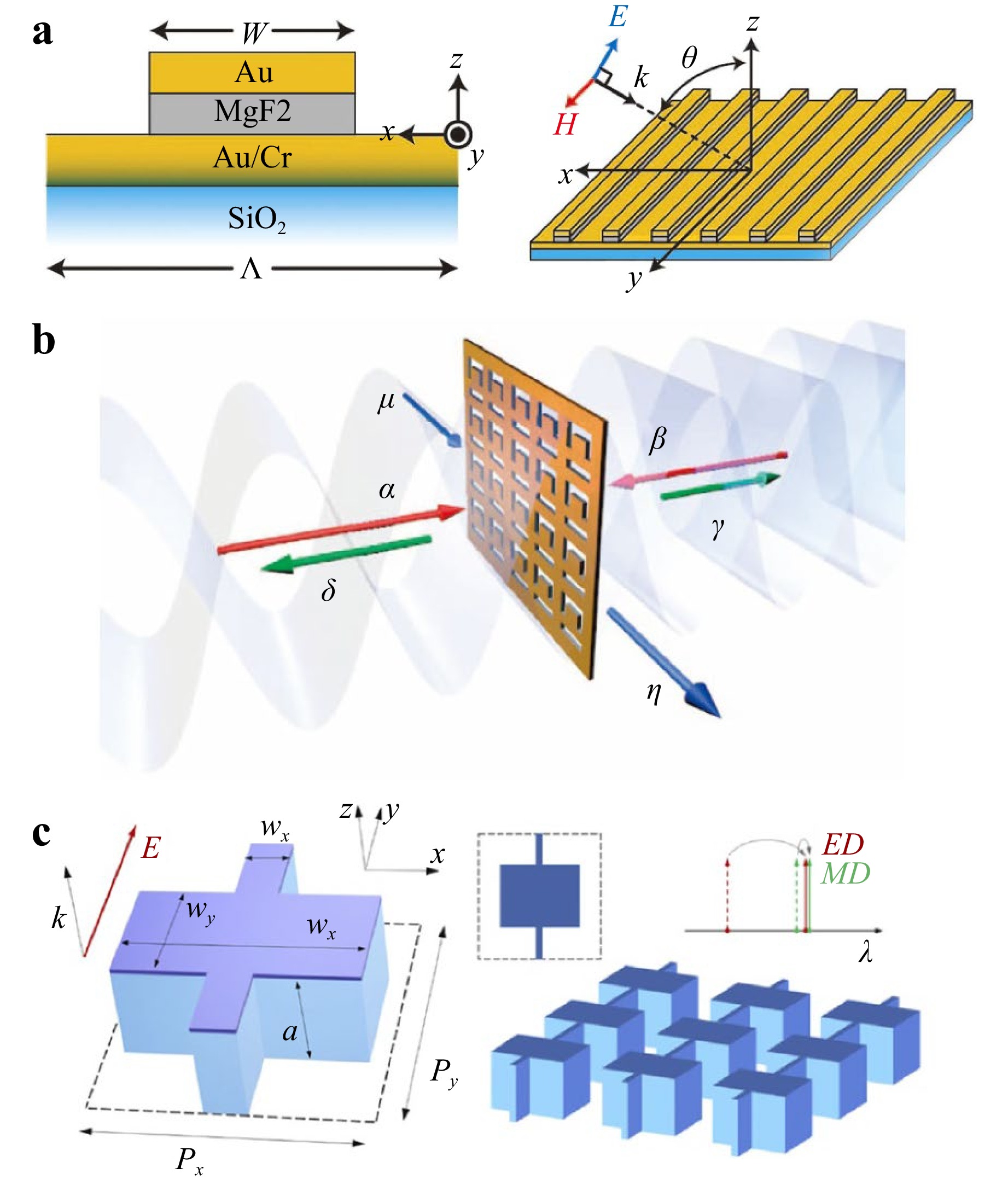
Fig. 10 Metasurface perfect absorber: Absorption enhancement by: a Localized plasmons115. b Single-photon-to-plasmon coupling116. Coherent perfect absorption enables the metasurface to achieve nearly 100% absorption at specific locations. c Degenerate electromagnetic dipole mode118. Broadband absorption achieved by tuning the interaction part of the nano-antenna.
-
In examining the quantum meta-devices, several promising research directions warrant comprehensive investigation. These emerging areas encompass quantum imaging, quantum metrology, quantum computing, and quantum communication, each representing distinct yet interconnected frontiers in quantum technology development. Here, we begin our discussion by focusing on quantum imaging, which serves as a fundamental cornerstone for understanding the broader implications of quantum meta-devices.
-
Quantum imaging exploits the temporal and spatial correlations of photon pairs and has demonstrated the capability to attain performance metrics that surpass those of conventional imaging systems. Grounded in the foundational principles of imaging, contemporary methods employing photon-pair-based quantum imaging can be classified into three categories50:
The first category is interference-based quantum imaging, characterized by the re-convergence of pump, signal, and reference lights in a second nonlinear crystal after passing through the first nonlinear crystal. This results in the indistinguishability of two SPDC processes, allowing light that has not interacted with the object to carry information about the object, which is ultimately reflected in the output interference fringes. The advantage of this method is the ability to use wavelengths that are undetectable for object interaction but detectable for collecting object information119.
The second category is correlation-based quantum measurement, with ghost imaging being a representative method. This approach utilizes the spatial correlation of photons generated by SPDC, which are produced at the same point with opposite transverse wave vectors. Therefore, the signal light can interact with the object, and a single-pixel detector can be used to collect the signal light, triggering the idler photon’s array detector to achieve the effect of taking a photo without the object. The advantage of this method is that it can theoretically achieve infinite angular resolution, thus enabling astronomical photography120.
The third category is entanglement-based quantum imaging, characterized by the interaction of non-classical two-photon states with objects to achieve higher imaging resolution and measurement precision. The N00N state mentioned when introducing the HOM effect is one such form. This method has already demonstrated its unique advantages in the field of biological imaging, namely obtaining clearer images with fewer detected photons121,122.
As an optical device that can perform flexible pattern mapping and phase control, the most direct application of metasurface in the field of quantum imaging is as a hologram123. Polarization entangled quantum imaging can be achieved by utilizing the multi-channel phase control characteristics of the metasurface124,125.
-
Quantum metrology seeks to exceed the precision limits of classical measurements by utilizing non-classical light, particularly through the use of entangled states, such as quantum N00N states126. A higher value of N enhances measurement precision, even when limited to a smaller number of measurements. In contrast to classical light, entangled photons can extract more information upon interacting with objects, leading to more accurate results.
Creating N00N states with N > 2 is challenging. To date, only the N = 2 N00N state can be deterministically generated through the HOM effect. To generate N00N states with N > 2, probabilistic pre-selection or post-selection is required, with success rates that exponentially decay with N127. Additionally, N00N states are susceptible to loss53. The polarization multiplexing property of the metasurface enables it to be used as a special beam splitter and thus can also be used to generate the HOM effect109.
-
Compared to classical computing, the advantages of quantum computing lie in two aspects: inherent parallelism and inherent security128. The first aspect significantly enhances the computational performance of quantum computers over classical ones, while the second ensures data security during extensive computations. Currently, the scalability of quantum computers is limited, and most researchers are dedicated to achieving the integration and coexistence of classical and quantum computing.
Researchers have demonstrated proof-of-principle quantum computations based on diffractive optical principles129. While these initial demonstrations validate the underlying theoretical framework, the transition toward practical applications necessitates substantial scaling of these systems.
-
Compared to traditional communication methods, the advantage of quantum communication lies in its security because one of the postulates of quantum mechanics is that measurement changes the quantum state. Therefore, if the two parties in communication share entangled photon pairs, one party can encode the polarization state of a single photon based on the information in hand and send unconditionally secure information to the other station130. Any eavesdropper’s measurement will disrupt the entangled state, thus being detected by the two parties in communication. Meta-devices, with their exceptional capabilities in wavefront manipulation and polarization control, are poised to make significant contributions to quantum communication applications.
-
In addition to the above, quantum applications also include quantum simulation131, quantum cryptography132, and quantum networks133. Among them, quantum random numbers are an important part of quantum cryptography. Quantum random numbers ensure the true randomness of the generated random numbers through the inherent probability of quantum mechanics and can be used in the encryption process to avoid theft and attacks. The ultra-compact nature of the metalens array makes it an integrable high-dimensional light source which can also be used as a high-density random number generator99.
-
Recent advances in meta-devices have shown promising applications in quantum optics, particularly in light source manipulation and interference control. While significant progress has been made in these areas, current technological limitations still remain challenges for further development. Notably, the fabrication of multilayer quantum meta-devices presents a significant bottleneck, primarily due to the complexity of multi-layer meta-device integration and precise alignment requirements. Furthermore, the implementation of meta-device detectors in quantum applications has been largely unexplored, with only a limited number of studies addressing this critical component. These constraints have impeded the full exploitation of meta-devices’ potential in quantum applications, particularly in achieving integrated quantum computation, sensing, and detection capabilities.
Meta-devices and metasurfaces are two sides of the same coin. Metasurfaces focus more on the physical mechanism, while meta-devices emphasize practical application value. A large number of studies on metasurface ensure the growth potential of meta-device in terms of applications. Currently, the majority of metasurface applications are rooted in quantum information theory; however, the quantum field itself encompasses much richer interpretations. Plasmonic metasurfaces, a traditional research focus within this domain, illustrate the interaction between electrons (fermions) and photons (bosons) and exhibit deeper physical implications compared to all-optical quantum systems. When intertwined with quantum plasma theory, concepts such as quantum size effects and quantum tunneling emerge, leading to potentially complex phenomena that warrant further exploration by researchers. A highly relevant topic in the field of quantum-integrated devices is the comparison between waveguide-integrated devices and metasurfaces. Waveguide-integrated devices offer a distinct advantage over metasurfaces by enabling the complete functionality of tasks ranging from light sourcing to quantum state manipulation and detection all on a single chip. This level of integration is notably challenging to achieve with current metasurface technology. On the other hand, metasurfaces excel in their scalability in terms of dimensions. This is because waveguide-integrated devices necessitate one directional light propagation, limiting expansion to an orthogonal direction. In contrast, light traverses through the thickness of a metasurface, allowing for expansion in any direction within the plane. A prominent application of this capability is the development of high-dimensional quantum light sources utilizing metalens arrays.
Several critical directions can be explored for advancing meta-device technologies. A particularly promising avenue involves the integration of meta-devices with waveguide-integrated platforms for enhanced modulation capabilities. This hybridization could enable precise control over quantum states while maintaining compact footprints. Furthermore, the incorporation of resonant meta-device onto detectors emerges as a crucial strategy for improving quantum efficiency. This approach could significantly enhance detection capabilities through field enhancement, potentially revolutionizing the performance of integrated quantum detectors.
The integration of quantum meta-devices with complementary technological approaches presents a compelling roadmap for next-generation quantum systems. Compared to liquid crystals or other planar optical elements, metasurfaces possess the advantage of having unit structures on a subwavelength scale, enabling flexible resonance control. This allows metasurfaces to achieve functionalities that are superior to other devices. For example, the enhancement effect of resonance on the light field can be utilized to construct entangled photon sources. However, the current drawback of metasurfaces lies in their limited programmability, whereas liquid crystals exhibit certain advantages in this aspect. Presently, some studies are exploring the combination of meta-devices with phase-change materials134,135 or liquid crystals136,137 to enhance the active tuning capabilities of meta-devices. As the field of quantum meta-devices continues to evolve, researchers can choose the meta-device they need based on different requirements. For example, if sensing is required or loss needs to be added to achieve a specific function, plasmonic meta-devices can be considered. If the function needs to be implemented based on phase modulation, dielectric meta-devices can be considered.
By synergistically combining the unique advantages of meta-devices, such as High-density integration, subwavelength manipulation, and precise wavefront control, with other quantum platforms, such as quantum dots138,139, it anticipates significant advances in integrated quantum technologies. This convergence could potentially address current limitations of meta-device while enabling highly compact, multifunctional quantum devices. The resulting hybrid systems are expected to facilitate seamless integration of quantum sources, processors, and detectors on a single platform, marking a crucial step toward practical quantum applications.
-
We acknowledge the support from the University Grants Committee / Research Grants Council of the Hong Kong Special Administrative Region, China [Project No. AoE/P-502/20, CRF Project: C5031-22G; C5078-24G, GRF Project: CityU11305223; CityU11300224; CityU11304925; CityU11305125], City University of Hong Kong [Project No. 9380131], and National Natural Science Foundation of China [Grant No. 62375232].
Quantum meta-devices
- Light: Advanced Manufacturing , Article number: (2025)
- Received: 16 January 2025
- Revised: 30 June 2025
- Accepted: 09 July 2025 Published online: 03 September 2025
doi: https://doi.org/10.37188/lam.2025.059
Abstract: Meta-devices, known for their capability to manipulate light fields at a subwavelength scale, have gained significant traction in the realm of quantum photonics in recent years. They are being utilized in miniaturized applications such as the preparation of quantum light sources and the control and detection of quantum states. In this review, we provide a systematic explanation of the working principles and notable applications of meta-devices in quantum optical information processing, while also outlining potential directions for the future development of quantum meta-devices.
Research Summary
Quantum meta-devices: Towards an integrable quantum optics platform
Meta-devices, prized for manipulating light at subwavelength scales, are emerging as pivotal tools in reducing the scale of quantum systems. While bulk optics are ideal quantum information carriers due to their coherence, ease of manipulation, and suitability for long-distance transmission, bulk optical platforms often suffer from large footprints. Professor Din Ping Tsai and his team detail how the ultrathin meta-devices, compatible with semiconductor processes, enable miniaturization and integration critical for scalable quantum technologies. Their review systematically showcases meta-device principles and applications, enabling key functions like generating scalable multi-photon sources, controlling large-scale interference networks, and building high-efficiency detection systems – all essential for advancing quantum communication, computing, sensing, and state control. This work also charts promising future directions for overcoming integration challenges in quantum meta-devices.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article′s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article′s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.






 DownLoad:
DownLoad: