-
Computer-generated hologram (CGH) provides a convenient approach to recording and reconstructing field information of lightwaves1–7. While conventional CGHs based on bulk materials meet physical bottlenecks in modern information technologies due to limited efficiency, resolution, and capacity, recently, the emerging field of nano-photonics has introduced new opportunities: meta-holograms, which can fundamentally improve CGH functions. The meta-holograms are the CGHs based on the metasurfaces, i.e., 2D arrays of optically thin nanostructures that can engineer light at will8–14. Owing to the signature light-manipulability of the metasurfaces, the meta-holograms present superior flexibility, resolution, and compactness, which can deliver a plethora of applications in virtual reality, data storage, and artificial intelligence15–30.
With the ever-growing demands for high capacity, small size, versatile functions, and secure transmission in modern optical devices, meta-holograms that can only reconstruct a single holographic image tend to become insufficient. Rather, the multiplexing meta-holograms that can simultaneously produce multiple independent holographic images on demand are desired and developed to serve these needs. Existing research efforts have demonstrated multiplexing holography technologies utilizing one or a few physically orthogonal dimensions of light to carry independent holography channels, thereby enhancing the capacity and security of the meta-holograms, including wavelength, linear momentum, orbital angular momentum (OAM), and polarization multiplexing, etc22,26,31–41.
Despite the special features provided by the aforementioned methods, they, however, are still constrained by limited potential for important performances. Indeed, with the increasing demands for higher capacity and better security, it is urgently needed to expand the multiplexing channels using two or more diversified orthogonal physical dimensions of light. Particularly, the previous works use phase-only or phase-polarization metasurfaces to accomplish multi-dimensional multiplexing, such as OAM multiplexing, fully polarization multiplexing, polarization-OAM multiplexing, etc22,42–50. However, on one hand, these metasurfaces still lack the essential capability to construct the ideal exact complex amplitude. Thus, their channel superposition is no longer linear and will suffer from substantial crosstalk and energy uniformity, which significantly constrain the number of operational channels35,51. More importantly, the incomplete spatial light modulation also limits the possible physical dimensions for holography multiplexing, making it challenging to achieve maximum possible multiplexing channels. On the other hand, the previously reported phase-polarization metasurfaces also use the structure parameters to control the transmitted light, so they have relatively narrower bandwidth with poorer fabrication tolerance.
In this work, we propose and experimentally demonstrate multi-dimensional multiplexing and encryption holograms based on dielectric broadband full-modulation geometric-phase metasurfaces. Such full-modulation dielectric geometric-phase metasurfaces are accomplished by the parallel tasking method, which can tailor the spatial amplitude, phase, and polarization of light simultaneously and independently with high robustness in broadband. Using the full-modulation metasurfaces, we employ the full Stokes polarization and the transverse momentum dimensions to multiplex multiple holographic images with deliberated information encryption. Compared to the common single-dimensional multiplexing principle, multi-dimensional multiplexing can significantly improve the capacity of the hologram. Moreover, the fully geometric-phase element design also grants the metasurface a much-desired broadband property with better fabrication tolerance. As a result, our proposed multi-dimensional multiplexing meta-hologram scheme paves the way for new nano-optoelectronic information technology boasting simultaneous high energy efficiency, spatial resolution, and broadband working wavelengths.
-
Our proposed broadband metasurface is accomplished by the parallel tasking method based on the geometric-phase principle52. The geometric-phase principle describes the relation between the phase shift of the transmitted light in the orthogonal polarization component and the in-plane orientation angle of an anisotropic element53,54. In particular, when left-/right-handed circularly polarized (LCP/RCP) light perpendicularly illuminates an anisotropic element with an in-plane rotating angle of θ, the orthogonal (converted) polarization component of the transmitted light relative to the incident polarization receives an additional $ \pm 2\theta $ phase delay53,54. Therefore, the geometric-phase metasurfaces are able to conveniently control the spatial phase of light through an inhomogeneous array, which is independent of the operation wavelength. The analytical derivation of the geometric-phase principle is appended in the Supplementary information.
While the geometric-phase metasurfaces can only tailor the phase profile of the transmitted light, here we present the full-modulation dielectric geometric-phase metasurface using the parallel tasking method. The goal of the full-modulation metasurface is to generate an arbitrary light beam $ {\mathbf{E}}\left( {x,y} \right) $ (arbitrary and customized spatial amplitude, spatial phase and spatial polarization distribution) with a complex profile at the nearfield of the metasurface transmission plane from an incident linear polarization (LP) plane wave $ {{{{\bf E}}}_{{\bf{in}}}} $, which can be expressed as
$$ {\bf E_{in}}=A_0\left[\begin{aligned}\sqrt 2 /2\\ \sqrt 2 /2\end{aligned}\right], {\bf E}(x,y)=A(x,y)e^{i\varphi(x,y)}\left[\begin{aligned}|E_l(x,y)|e^{-i\delta(x,y)/2}\\|E_r(x,y)|e^{i\delta(x,y)/2}\end{aligned}\right] $$ (1) where $ {A_0} $ is the amplitude of the incident LP plane wave, $ A\left( {x,y} \right) $, $ \varphi \left( {x,y} \right) $, $ \left| {{E_l}\left( {x,y} \right)} \right| $, $ \left| {{E_r}\left( {x,y} \right)} \right| $ and $ \delta \left( {x,y} \right) $ are the amplitude profile, phase profile, normalized amplitude profile of the LCP component, normalized amplitude profile of the RCP component, and relative phase difference profile between the LCP and RCP components of the produced arbitrary light beam, respectively. Note that, for mathematical convenience, the incident LP plane wave and produced arbitrary light beam are both presented in vector forms based on the circular polarization (CP) basis.
The proposed mechanism of the parallel tasking method is illustrated in Fig. 1. We introduce the supercell with 2 × 2 unitcells (anisotropic elements) as the building block of the metasurface and divide the rotating angle of each unitcell into three sub-angles $ {\theta _\varphi } $,$ {\theta _i} $ and $ {\theta _s} $ as linear superposition. The $ {\theta _\varphi } $ is used to modulate the phase profile, the $ {\theta _i} $ is used to modulate the amplitude profile based on the interference between two adjacent units, and the $ {\theta _s} $ is used to modulate the polarization profile based on the interference between two adjacent rows. The relationship between the transmitted light and the rotating angle of the unitcells can be expressed as:
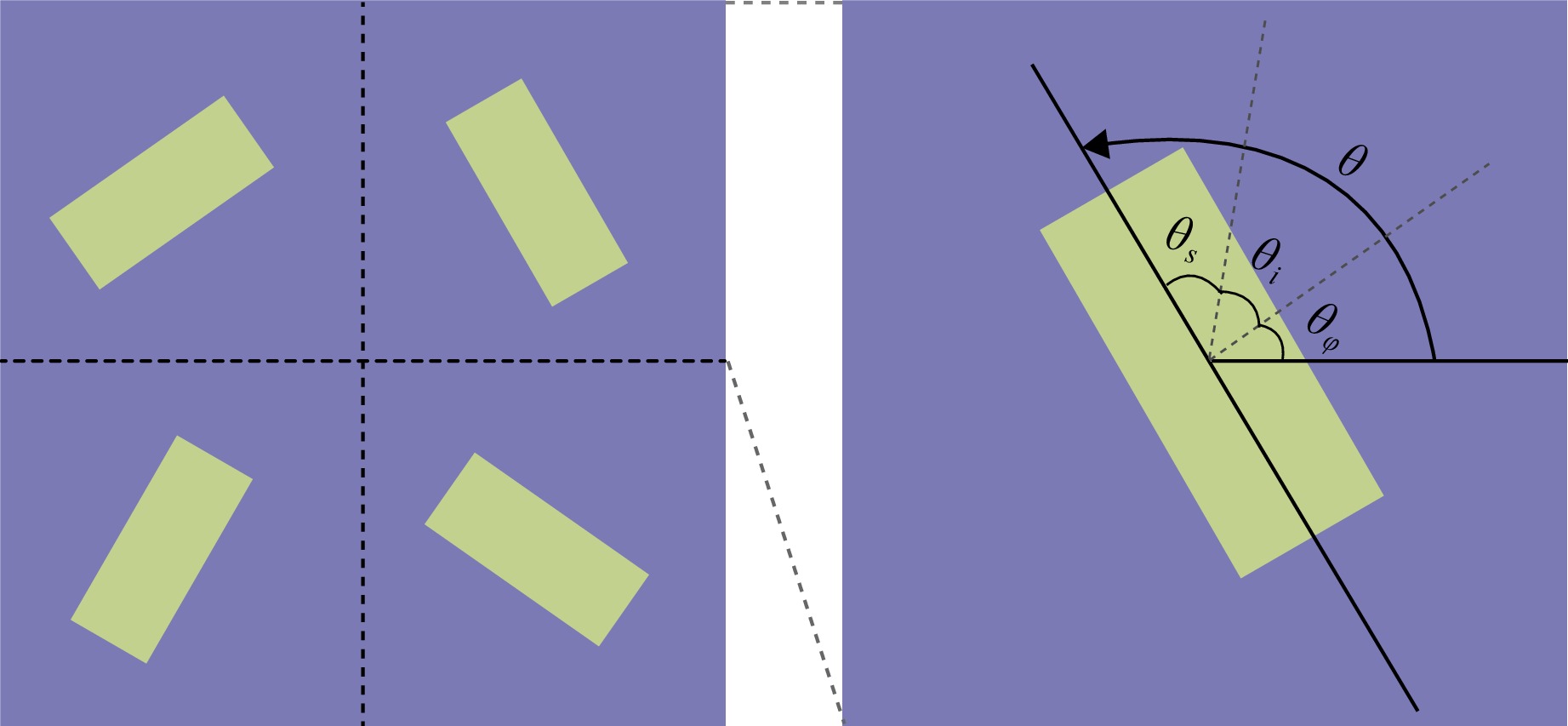
Fig. 1 Schematic illustration of the parallel tasking method. The supercell with 2 × 2 unitcells is used as the building block of metasurfaces and the rotating angle of each unitcell is divided into three sub-angles for parallel tasks, i.e. with $ {\theta _\varphi } $ for phase modulation (geometric phase), $ {\theta _i} $ for amplitude modulation (interference by adjacent unitcells in a row), and $ {\theta _s} $ for polarization modulation (orthogonal polarization combination by odd and even rows).
$$ \begin{aligned} {\theta _1} =\;& {\theta _{1\varphi }} + {\theta _{1i}} + {\theta _{1s}} \\=\;& \frac{{{\varphi _{\text{0}}}\left( {x,y} \right) + {\delta _{\text{0}}}\left( {x,y} \right)/2 + \arccos [{A_{\text{0}}}\left( {x,y} \right)\left| {{E_r}\left( {x,y} \right)} \right|]}}{2} + kx \\ {\theta _2} =\;& {\theta _{2\varphi }} + {\theta _{2i}} + {\theta _{2s}} \\=\;& \frac{{{\varphi _{\text{0}}}\left( {x,y} \right) + {\delta _{\text{0}}}\left( {x,y} \right)/2 - \arccos [{A_{\text{0}}}\left( {x,y} \right)\left| {{E_r}\left( {x,y} \right)} \right|]}}{2} + kx \\ {\theta _3} =\;& {\theta _{3\varphi }} + {\theta _{3i}} + {\theta _{3s}} \\=\;& - \frac{{{\varphi _{\text{0}}}\left( {x,y} \right) - {\delta _{\text{0}}}\left( {x,y} \right)/2 - \arccos [{A_{\text{0}}}\left( {x,y} \right)\left| {{E_l}\left( {x,y} \right)} \right|]}}{2} - kx \\ {\theta _4} =\;& {\theta _{4\varphi }} + {\theta _{4i}} + {\theta _{4s}} \\=\;& - \frac{{{\varphi _{\text{0}}}\left( {x,y} \right) - {\delta _{\text{0}}}\left( {x,y} \right)/2 + \arccos [{A_{\text{0}}}\left( {x,y} \right)\left| {{E_l}\left( {x,y} \right)} \right|]}}{2} - kx \end{aligned} $$ (2) Generally, the sub-angles of a geometric phase element and hence the consequent geometric phases function independently of each other, while the sequence of the angles does not matter. This principle is similar to multi-level diffraction14.
Thus, by using the parallel tasking method, we can achieve full modulation, i.e., independent and arbitrary full modulation of phase, amplitude and polarization. More details of the full-modulation metasurface are presented in the Supplementary information. In particular, since the phase, amplitude and polarization profiles are only related to the rotating angle of each unitcell, our full-modulation metasurface can work in broadband with high robustness.
-
Here, we present a general way of viewing the diffraction of the multi-dimensional multiplexing hologram from the hologram plane to the image plane. Indeed, we use the Fourier CGH in this work. Thus, the relationship of electric fields between the image plane and the hologram plane for a single holography can be expressed as
$$\begin{aligned} {\mathbf{E}}_{{\text{img}}}^{}({x_2},{y_2}) =\;& {F} ({\mathbf{E}}_{\text{A}}^{}({x_1},{y_1}))\\=\;& {\iint {{{\mathbf{E}}_{\text{A}}}({x_1},{y_1}){e^{ - i2\pi({x_2}{x_1}/\lambda f + {y_2}{y_1}/\lambda f)}}d{x_1}dy}_1} \end{aligned}$$ (3) where $ ({x_1},{y_1}) $ and $ ({x_2},{y_2}) $ represent the coordinates in the Cartesian coordinate system on the hologram plane and the image plane, respectively, $ {\mathbf{E}}_{{\text{img}}}^{} $ is the electric field on the image plane, $ {\mathbf{E}}_{\text{A}}^{} $ is the electric field on the hologram plane, λ is the wavelength of the incident beam, f is the focal distance of the lens, and $ {F} () $ denotes Fourier transform. Mathematically, the multi-dimensional multiplexing hologram can be expressed as the linear superposition of electric fields of multiple holograms with different transverse momenta and polarization. It can be expressed as
$$ {{\vec {\bf E}}}_{{\text{meta}}}^{{\text{mul}}} = \sum\limits_{j = 1:N} {{E_j}} \cdot {{{\hat {\bf p}}}_j} \cdot {e^{i{{{{\vec {\bf k}}}}_j} \cdot {{\vec {\bf r}}}}} $$ (4) Here, $ {{\vec {\bf E}}}_{{\text{meta}}}^{{\text{mul}}} $ is the electric field of the multi-dimensional multiplexing hologram, $ {E_j} $ is the electric field of the j-th hologram, $ {{{\hat {\bf p}}}_j} $ is the polarization of the j-th hologram, $ {{{\vec {\bf k}}}_j} $ is the phase gradient of the j-th hologram, $ {{\vec {\bf r}}} = ({x_1},{y_1}) $ is the coordinates on the metasurface plane, and N is the number of the multiplexing holograms.
Remarkably, it is straightforward that the $ {{\vec {\bf E}}}_{{\text{meta}}}^{{\text{mul}}} $ is a pattern with complex amplitude, phase and polarization distribution. To fully record the information of the multi-dimensional multiplexing hologram, we need a metasurface that can simultaneously and independently tailor the spatial amplitude, phase and polarization profile of the transmitted beam. Hence, the profile on the metasurface plane can be expressed as
$$ {\bf E}_{{\text{meta}}}^{{\text{mul}}} = {A_0}(x,y){e^{i{\varphi _0}(x,y)}}\left[ {\begin{array}{*{20}{c}} {\left| {{E_x}(x,y)} \right|{e^{ - i{\delta _0}(x,y)/2}}} \\ {\left| {{E_y}(x,y)} \right|{e^{i{\delta _0}(x,y)/2}}} \end{array}} \right] $$ (5) Here, $ {A_{\text{0}}}(x,y) $, $ {\varphi _{\text{0}}}(x,y) $, $ \left| {{E_x}(x,y)} \right| $, $ \left| {{E_y}(x,y)} \right| $ and $ {\delta _{\text{0}}}(x,y) $ are the amplitude, phase, unit x-/y-linearly polarized light amplitude, and relative phase difference profiles between x- and y-linear polarization components of the produced beam, respectively. Note that Eq. 5 in the LP basis can also be expressed as Eq. 1 in the CP basis.
The general concept of the proposed multi-dimensional multiplexing meta-holography enabled by the full-modulation dielectric geometric-phase metasurface is depicted in Fig. 2. Indeed, a pre-designed fabricated metasurface encodes the intended multiplexing information, manifested as the holographic images of 6 letters “H, S, A, B, U, T”. Depending on the specific reading conditions (i.e., the incident/transmitted polarizations and directions, etc.), the metasurface selectively exhibits the corresponding images within the designated channels. We emphasize that such a concept only illustrates rather simple schematics for presentation convenience. In principle, these conditions can be expanded to accommodate many more input/output directions or employ other multiplexing dimensions. Considering the enormous possible combinations of input/output conditions, the proposed meta-holography can support a very sophisticated holography multiplexing/demultiplexing strategy, as will be elaborated later in this work. Moreover, since we adopt a full-modulation pure geometric-phase metasurface approach, owing to the featured dispersion-less property, we expect a broadband performance for the proposed meta-holography, as will also be experimentally demonstrated later in this work.
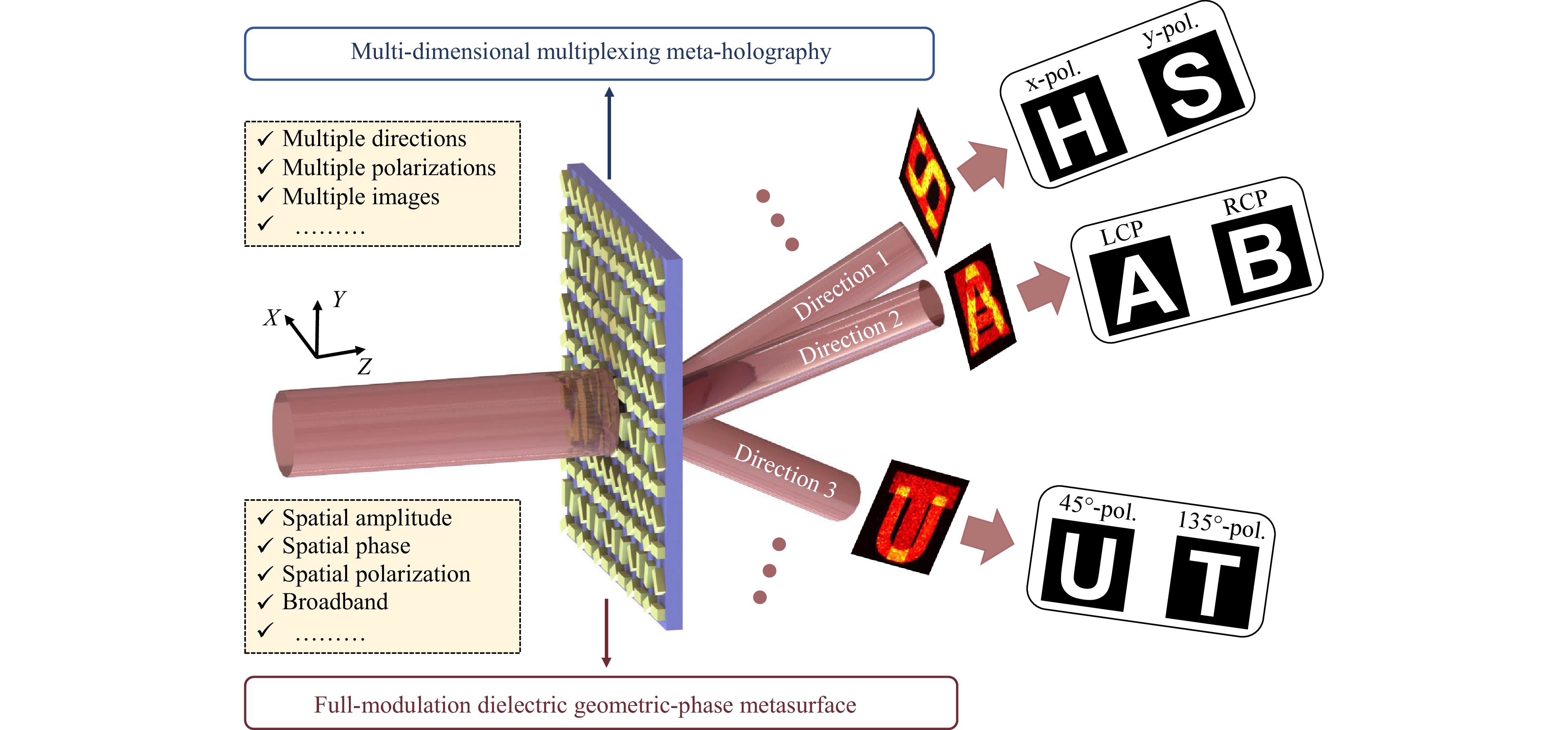
Fig. 2 The concept of the multi-dimensional multiplexing meta-hologram is enabled by the full-modulation dielectric geometric-phase metasurface. As an illustrative example, for the hologram of 6 letters “ABHUST”, each letter has a unique polarization and propagating direction as an independent channel.
-
In this work, we propose a high-efficiency dielectric geometric-phase metasurface to implement multi-dimensional multiplexing holograms that simultaneously encode full Stokes polarization and transverse momentum.
To build the proposed meta-hologram, the first step is to design the unitcell of the metasurface. Here, we design the unitcell which has a silicon nitride nanobar with 320 nm × 100 nm × 600 nm and a 380 nm × 380 nm SiO2 substrate (as a period) as the geometric-phase element, as shown in Fig. 3a. Then, we use the Lumerical FDTD solution software to simulate the electromagnetic response of the designed dielectric silicon nitride nanobar in the broadband visible range. As shown in Fig. 3e, the transmission phase spectrum of this element exhibits a significant phase difference between the transverse-electric (TE) and transverse-magnetic (TM) polarized illumination, while the transmission efficiency is nearly unity out of the resonance region. Such a feature is desired for the geometric-phase element to achieve high polarization conversion efficiency (PCE), which is defined as the power ratio of the converted polarization component of the transmitted beam to the incident beam. Then, we calculate the PCE, which is plotted in Fig. 3f. Next, as shown in Fig. 3h, to verify the phase modulation of the designed element, we numerically simulate its transmission phase spectrum of the orthogonally polarized light under LCP illumination versus the in-plane rotation of the element. The results show excellent agreement with the expectation from the geometric-phase principle.
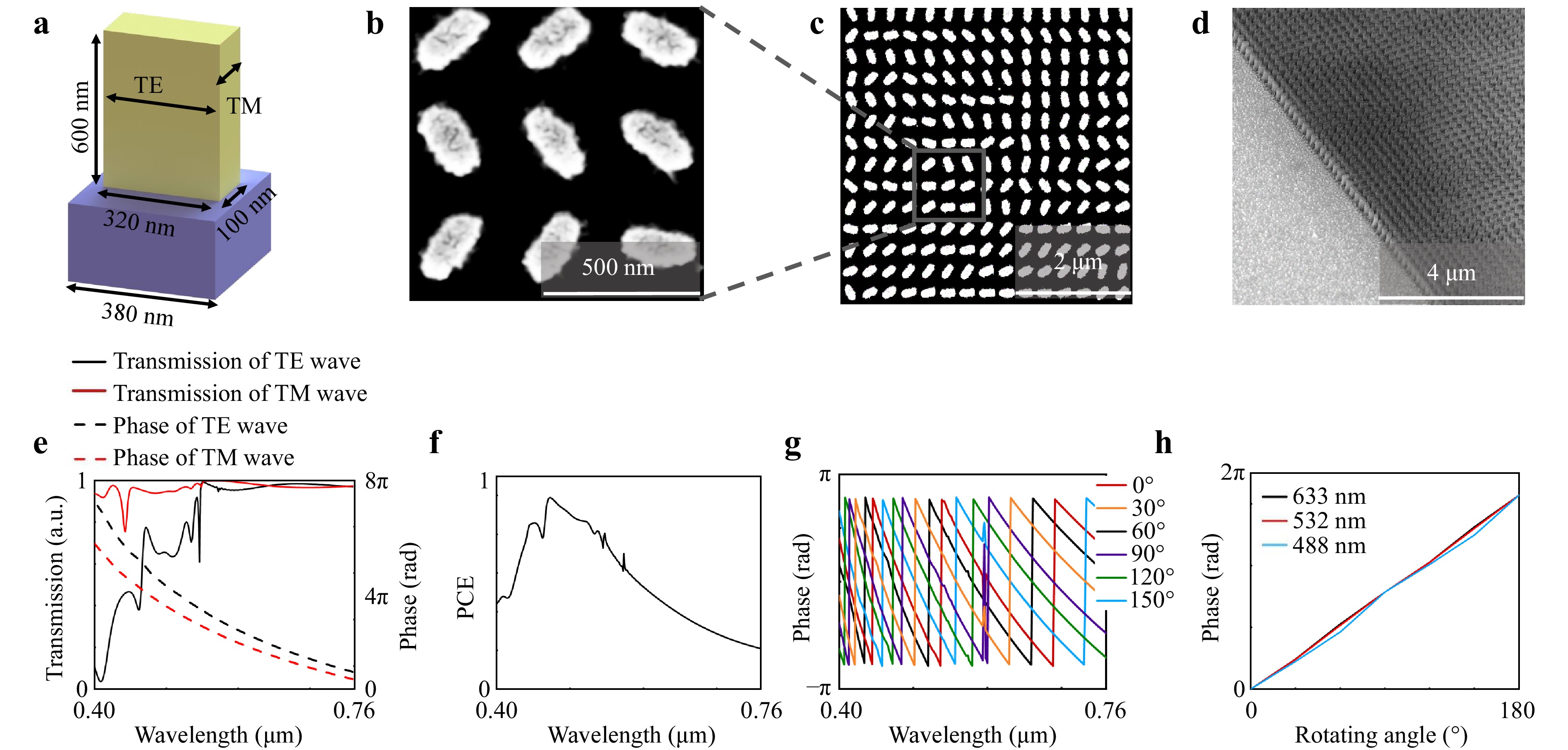
Fig. 3 The dielectric geometric-phase metasurfaces and their electromagnetic response. a The schematic diagram of a dielectric nanobar antenna unitcell. b-d The SEM images of the fabricated metasurface sample. e Simulated transmission and phase responses of the dielectric nanobar under TE (X-pol) and TM (Y-pol) linear polarizations from 400 to 760 nm. f The polarization conversion efficiency (PCE) of the dielectric geometric-phase element. g Phase shift versus wavelength and the rotating angle. h Phase shift versus rotating angle of the dielectric nanobar element.
The second step is to use the parallel tasking method to establish the geometric-phase metasurfaces to modulate the spatial amplitude, phase, and polarization simultaneously and independently. As described above, we divide the total in-plane rotation angle of each geometric-phase element into three sub-angles $ {\theta _\varphi } $, $ {\theta _i} $ and $ {\theta _s} $. Therefore, the metasurface can fully modulate the spatial light (spatial phase, spatial amplitude, spatial polarization).
The third and final step is to design and experimentally demonstrate the proposed multi-dimensional multiplexing meta-hologram on the hologram plane. Here, as a representative example, we design the hologram of 6 letters “ABHUST” and each letter has a unique polarization and propagation direction. Fig. 2 presents the schematic illustration of the multiplexing meta-hologram enabled by the full-modulation geometric-phase metasurface. The electric field profile $ {{\vec {\bf E}}}_{{\text{meta}}}^{{\text{mul}}} $ of the multi-dimensional multiplexing hologram is the superposition of multiple channels, which can be expressed as
$$ \begin{aligned} {\vec {\bf E}}_{\text{meta}}^{\text{mul}} =\;& \sum\limits_{j = 1:N} {E_j} \cdot {{\hat {\bf p}}_j} \cdot e^{i{{\vec {\bf k}}_j} \cdot {{\vec {\bf r}}}} \\ =\;& {E_A}{e^{i{{{\vec {\bf k}}}_1} \cdot x}}\left[ {\begin{array}{*{20}{c}} 1 \\ i \end{array}} \right]/\sqrt 2 + {E_B}{e^{i{{{{\vec {\bf k}}}}_1} \cdot x}}\left[ {\begin{array}{*{20}{c}} 1 \\ { - i} \end{array}} \right]/\sqrt 2 \\&+ {E_H}{e^{i{{{{\vec {\bf k}}}}_2} \cdot y}}\left[ {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right] + {E_s}{e^{i{{{{\vec {\bf k}}}}_2} \cdot y}}\left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right] \\ & + {E_U}{e^{i{{{{\vec {\bf k}}}}_3} \cdot (x + y)}}\left[ {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right]/\sqrt 2 + {E_T}{e^{i{{{{\vec {\bf k}}}}_3} \cdot (x + y)}}\left[ {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right]/\sqrt 2 \end{aligned} $$ (6) The detailed electric field distributions are provided in the Supplementary information. This distribution exhibits complexity that necessitates a full modulation of the spatial amplitude, phase, and polarization. We emphasize that here the amplitude profile of each channel, which indicates the power distribution in different channels, can be independently and freely controlled. This property is an important signature of full-dimensional modulation multiplexing in this work that is not possible in conventional phase-only or phase-polarization modulation multiplexing. The total size of the metasurface is approximately 389 μm × 389 μm with 1024 × 1024 unitcells. The field recorded in the metasurface is a Fourier transform of the picture in the camera. Thus, the size of the “ABHUST” in the camera is decided by the focal length of the lens and the size of the metasurface. Additionally, the resolution of the generated holographic images is ultimately determined by the functional pixels of the metasurfaces, i.e., the super-cell. It could be significantly increased when the total number of pixels is increased.
-
To experimentally validate the broadband multi-dimensional multiplexing holography, we fabricate a meta-hologram sample and obtain the scanning electron microscopy (SEM) image as shown in Fig. 3b-d. The detailed mathematical framework for the multiplexing process is provided in the Supplementary information. In the following, we demonstrate 3 typical scenarios to exhibit the distinct functionalities of encoding and reconstructing all the holographic information with a single metasurface sample.
-
Firstly, we show the schematic illustration of FIVO in Fig. 4a. In this scenario, we set a fixed incident beam, which is x-linearly polarized and normally illuminates the metasurface, and expect multiple transmission beams as the varied designated channels. Such a scenario can potentially lead to multi-casting applications in which a metasurface chip can broadcast particular information to different users.
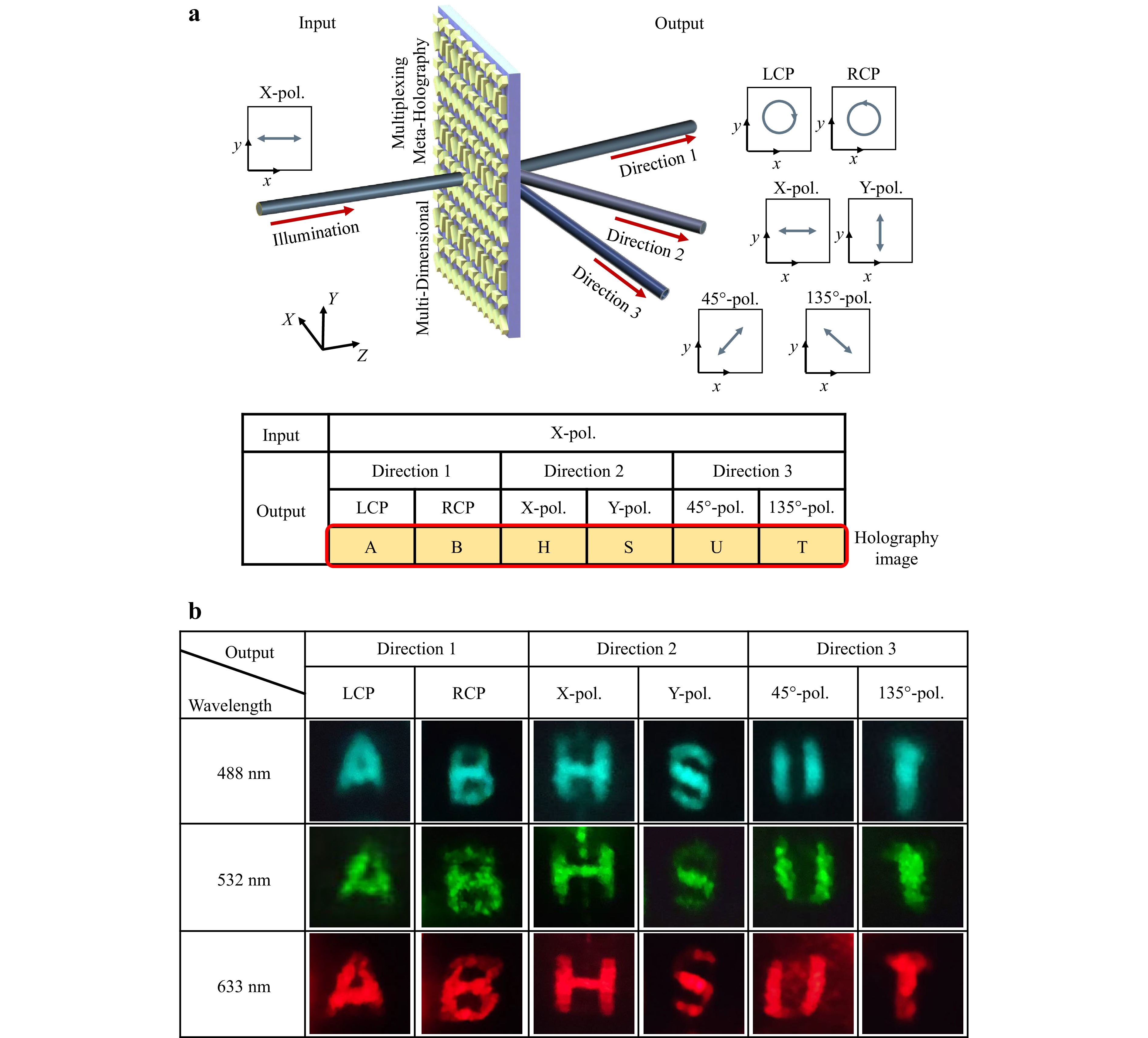
Fig. 4 Schematic illustration and experimental results of the fixed input & varied output (FIVO) scenario. a Schematic illustration of the multi-dimensional multiplexing hologram under x-LP illumination. The red arrows refer to the input and output directions, and the blue arrows refer to the polarization states of the incident and transmitted beams. b Experimental measurement results on the image plane at different wavelengths (488 nm, 532 nm, 633 nm).
Accordingly, the final holographic images on the image plane can be expressed as
$$ {\vec{\bf E}}_{\text{image}}^{}={\displaystyle \sum _{j=1:N}\mathrm{F}({E}_{j}})\otimes \mathrm{F}({\hat{\bf p}}_{j})\otimes \mathrm{F}({e}^{i{\vec{\bf k}}_{j}\cdot \vec{\bf r}}) $$ (7) Here, ‘$ \otimes $’ is the convolution operator, $ \otimes {\rm F} ({{{\hat {\bf p}}}_j}) $ = $ {{{\hat {\bf p}}}_j} $, and the transformation of the $ {e^{i{{{{\vec {\rm k}}}}_j} \cdot {{\vec {\bf r}}}}} $ can be expressed as:
$$ \mathrm{F}({e}^{i{\overrightarrow{\bf k}}_{j}\cdot \overrightarrow{\bf r}})=\delta \left(\frac{{\overrightarrow{\bf k}}_{j}\lambda f}{2\pi }\right) $$ (8) where $ \delta $ is the Dirac impulse function. Hence, the electric field on the image plane is
$$ {{\vec {\bf E}}}_{{\text{image}}}^{{\text{mul}}} = \sum\limits_{j = 1:N} {{\rm F} ({E_j}} ){{{\hat {\bf p}}}_j} \otimes \delta \left(\frac{{{{{{\vec {\bf k}}}}_j}\lambda f}}{{2\pi }}\right) $$ (9) Eq. 9 shows the multiplexed electric field on the image plane. Indeed, the different holographic images with different polarizations will appear at different positions.
This expectation is demonstrated by Fig. 4b, in which the symbols ‘A’/ ‘B’ with LCP/RCP are shown on the left (Direction 1). Similarly, the middle section (Direction 2) exhibits the symbols ‘H’ and ‘S’ in x-/y- linear polarization, respectively. Moreover, the symbols ‘U’ and ‘T’ can be observed in 45°/135° linear polarization on the right (Direction 3), respectively. As shown in Fig. 4b, this phenomenon can be witnessed at 488 nm, 532 nm and 633 nm, respectively, indicating a much-desired broadband operation capability as expected for the geometric-phase metasurface.
-
Secondly, we depict the schematic illustration of VIFO in Fig. 5a. In this scenario, we use different incident beams with different polarizations and directions, and a fixed transmission path (normal to the metasurface) is selected as the output. We expect that the transmitted beam will exhibit a unique hologram depending on the particular input conditions. Considering a sheet label capable of displaying different images under varying illumination conditions, this mechanism can enable potential applications in laser anti-counterfeiting.
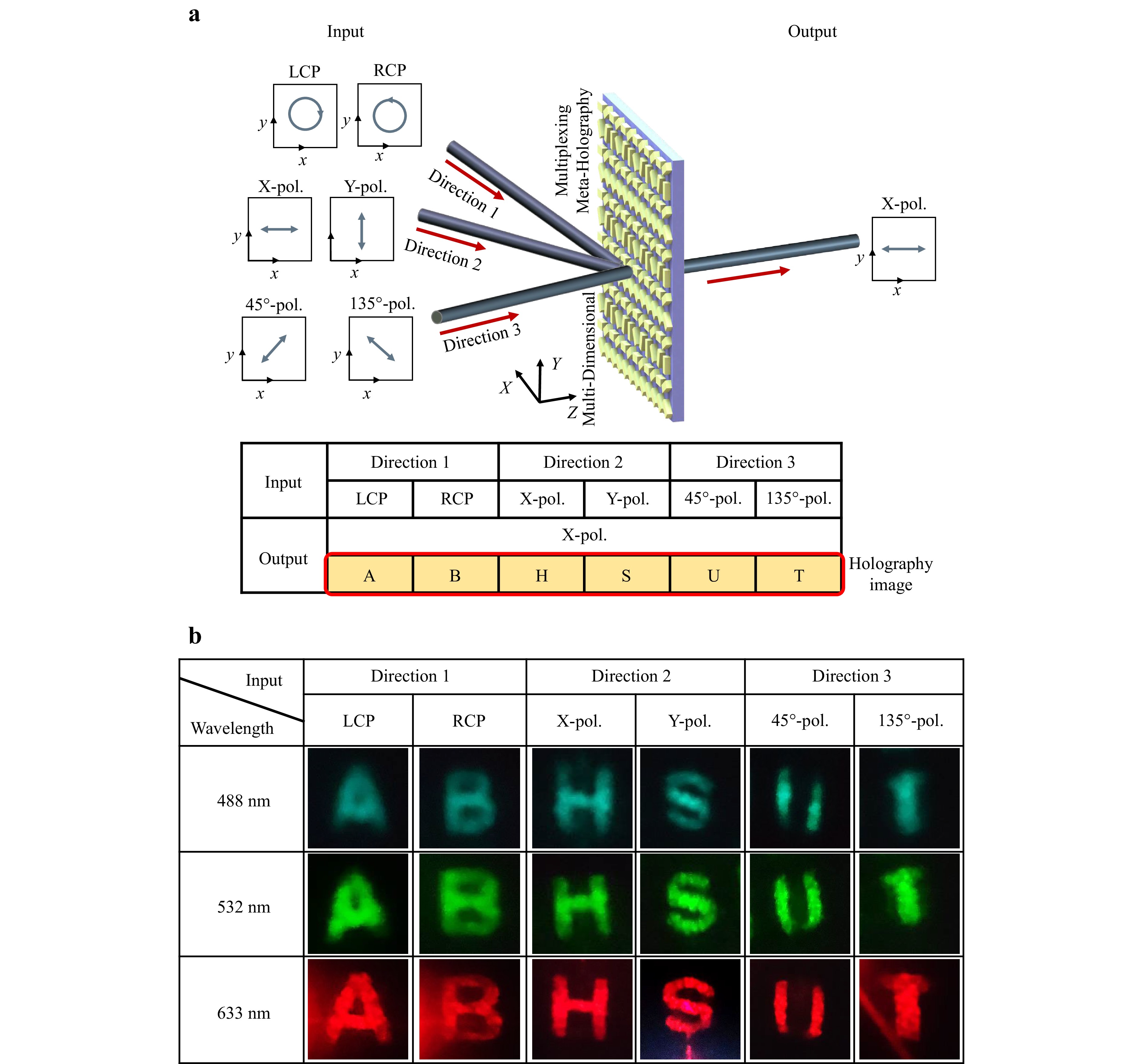
Fig. 5 Schematic illustration and experimental results of the varied input & fixed output (VIFO) scenario. a Schematic illustration of the multi-dimensional multiplexing hologram. The red arrows refer to the input and output directions. The blue arrows refer to the polarization states of the incident and transmitted beams. b Experimental measurement results on the image plane at different wavelengths (488 nm, 532 nm, 633 nm).
The transmitted beam of the metasurface demodulation can be expressed as
$$\begin{aligned} {{\vec {\bf E}}}_{{\text{meta}}}^{{\text{Demux}}} =\;& {{\vec {\bf E}}}_{{\text{meta}}}^{{\text{mul}}} \cdot {\hat p_a} \cdot {e^{ - i{{\vec k}_a} \cdot \vec r}} = {E_{{\text{holo}}\_a}}{\hat p_x} \\&+ \sum\limits_{j = 1:N,j \ne a} {{E_{{\text{holo}}\_j}} \cdot {{\hat p'}_j}} \cdot {e^{i{{\vec k}_j} \cdot \vec r}} \cdot {\hat p_a} \cdot {e^{ - i{{\vec k}_a} \cdot \vec r}} \end{aligned}$$ (10) where $ {\hat p'_j} $ is the polarization state of the j-th channel under $ {\hat p_a} $ light illumination. Then, we use a polarizer with 0° rotation angle on the transmission side and use an aperture to let the light whose propagating direction is vertical to the plane pass through. The holographic image on the image plane can be expressed as
$$ {{\vec {\bf E}}}_{{\text{image}}}^{{\text{re}}}({x_2},{y_2}) = {F} ({E_{{\text{holo}}\_a}}) $$ (11) $ {{\vec {\bf E}}}_{{\text{image}}}^{{\text{re}}} $ is the received image on the imaging plane. It indicates that different polarized light with different incident angles can produce different images on the image plane.
Likewise, we show the experimental results in Fig. 5b at different wavelengths of 488 nm, 532 nm and 633 nm, respectively, as an important confirmation of the broadband operation property of the geometric-phase metasurface.
-
Finally, we show the schematic illustration of the most complex VIVO in Fig. 6a. In this scenario, both the input and output have varied conditions: the incident beam can have different polarizations, while the transmitted beams can have different polarizations and directions. Different holographic images can then be delivered based on the particular combinations of the input and output conditions. This scenario can potentially lead to optical encryption applications, in which the user must know the correct way to illuminate the metasurface and read the hologram channel to eventually acquire the encoded information.
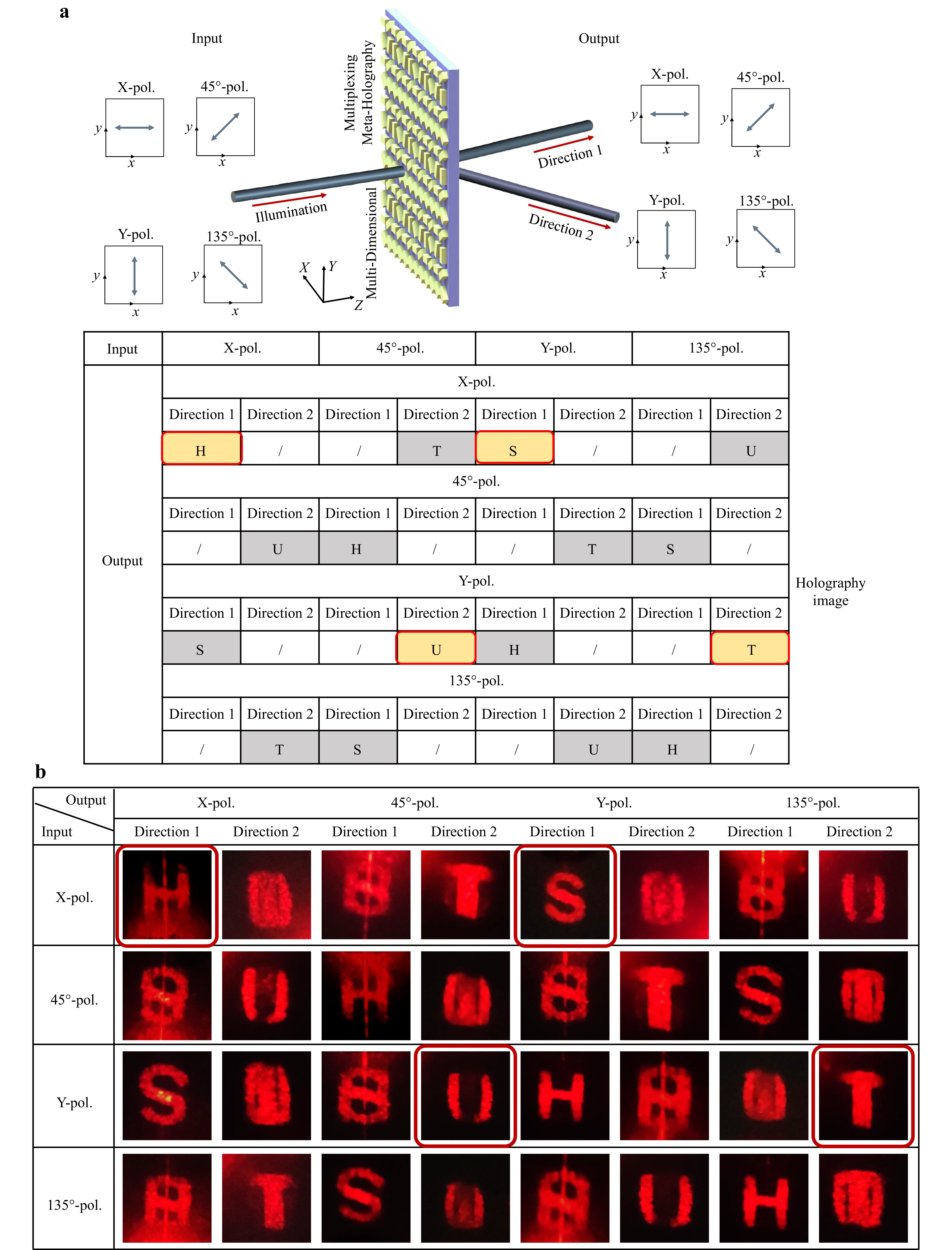
Fig. 6 Schematic illustration and experimental results of the varied input & varied output (VIVO) scenario. a Schematic illustration of the multi-dimensional multiplexing hologram encryption. The red arrows refer to the input and output directions. The blue arrows refer to the polarization states of the incident and transmission beams. b Experimental measurement results on the image plane.
Here, as an example, we conceal the word “HUST” in the metasurface. As shown in Fig. 6a, we set the pre-determined input/output conditions (i.e., the decryption key) as x-pol/x-pol direction 1 (for “H”), 45°-pol/y-pol direction 2 (for “U”), y-pol/x-pol direction 1 (for “S”), and 135°-pol/y-pol direction 2 (for “T”), respectively, then the concealed word can be read out correctly out. If the reading conditions are incorrect, the receiver will be likely to either get a noisy image (as a hybrid pattern of two holographic images) as indicated by the “/” sign, or get a misleading false image as indicated by the gray background in Fig. 6a. In practice, one can implement more images with a specific reading sequence in the meta-holography. Considering the vast number of time-varied reading orders, it is almost impossible for a hacker to “guess” the intended information stored in the metasurface.
The experimental measurement results on the image plane are shown in Fig. 6b. The red boxes mark the concealed word “HUST” that is read out under the correct reading conditions. Notably, certain crosstalk between different channels, e.g., in Fig. 6b x-pol input/x-pol direction 2 output condition, etc, can be observed, which is due to the mixing of the holographic images in non-orthogonal channels. Note that not all illustrated channels in the experiment are mutually orthogonal, e.g., the 45°-pol channel is related to both x-pol and y-pol channels, and their holographic images naturally exhibit the trend of image mixtures. Although non-orthogonal channels cannot directly increase the information storage capacity, they can still be meaningful for enhancing encryption complexity and improving data security.
-
Here, we discuss some important notes about the multi-dimensional multiplexing meta-holograms based on the full-modulation dielectric geometric-phase metasurfaces.
Firstly, energy uniformity (EU), commonly defined as the average power difference across each channel, is a critical parameter for evaluating the performance of a multiplexing hologram system51.
$$ \text{EU}=\frac{1}{N}{\displaystyle \sum _{j=1:N}\left|({P}_{j}-\overline{P})\right|} $$ (12) where $ {P_j} $ is the power of the j-th channel and $ \bar P $ is the average power of the multiplexing channels. The minimal EU, i.e., all channels share the same power, may indicate an ideal power allocation of the multiplexing system. For conventional phase-only and phase-polarization metasurfaces, since they do not include direct amplitude modulation, they cannot completely control the amplitude profile of the multiplexing channels, thus the power distribution to each channel can be different. As a result, their EUs are typically non-trivial, leading to a deteriorated multiplexing performance. Moreover, the EU of the conventional phase-only and phase-polarization metasurfaces will inevitably decrease with the increase of the channel number, thus limiting the maximum number of operational multiplexing channels51. In comparison, the proposed full-dimensional modulation metasurfaces can accurately record the full information of the multiplexing holography. Hence, it can, in principle, equally allocate the power to each channel and achieve an ideal EU. We have appended a detailed discussion in the Supplementary information.
Next, we discuss the signal-to-noise ratio (SNR) of multiplexing holographic images based on the different multiplexing methods. Here, we only concentrate on the noise caused by the multiplexing methods. Since the phase-only and phase-polarization metasurfaces often neglect the amplitude information, the missing amplitude information will induce substantial crosstalk due to the non-exact reproduction of the de-multiplexing operation. This kind of crosstalk tends to be stronger between adjacent channels, which will eventually limit the density of the spatial multiplexing system. Furthermore, similarly to the EU, the crosstalk of phase-only and phase-polarization metasurfaces will also increase with the channel number51. As a comparison, the full-dimensional spatial light modulation meta-hologram can always achieve theoretical minimum crosstalk for the full-dimensional recording of image information, regardless of the channel number. The details are discussed in the Supplementary information.
Thirdly, we introduce the multiplexing efficiency to evaluate different multiplexing methods. Here we define the multiplexing efficiency as the efficiency of the multiplexing technology itself rather than the meta-hologram efficiency as
$$ Eff = \frac{{\displaystyle\sum\limits_{j = 1:N} {{P_j}} }}{{{P_{inc}}}} $$ (13) where $ {P_{inc}} $ is the incident power. Here, we focus on the efficiency of the hologram methods themselves, rather than the element efficiency of the geometric-phase element. The phase-only and phase-polarization metasurface multiplexing holography can transform all of the light incident into the final multiplexing image. Considering the EU on each channel, the efficiency for each channel on the phase-only and phase-polarization metasurface is ~1/N. However, the full-dimensional metasurfaces can provide an ideal efficiency distribution in theory and each channel can get 1/N energy of the transmitted beam. However, in reality, the amplitude modulation in the passive metasurface always introduces extra power loss, so the transmission beam is always less than the incident beam. So each channel of the meta-hologram can get less than 1/N of the total incident power.
Subsequently, we discuss the diffraction efficiency (DE) of the proposed multiplexing holographic. The proposed polarization-phase metasurface adopts a dielectric nanobar as geometric units. As illustrated in Fig. 3f, we demonstrate that the PCE reaches 0.9 at a 600 nm wavelength through rigorous electromagnetic simulation. However, this efficiency exhibits wavelength-dependent characteristics, decreasing to 0.1 at 480 nm. Notably, the parallel tasking methodology introduces an inherent 50% energy loss during polarization multiplexing52. Taking these factors into account, the overall DE can be quantitatively expressed as:
$$ DE \leqslant PCE \times {\text{amp}} \times 50{\text{%}} $$ (14) where PCE denotes polarization conversion efficiency, and amp represents amplitude modulation efficiency. In addition, it is important to note that although fabrication errors (dimensional deviations) may influence the overall DE by reducing the PCE, the optical field modulation (amplitude, phase, and polarization) can still be accurately controlled. This is because the proposed geometric phase-based full-dimensional metasurface primarily relies on the rotation angles of the units to achieve full-dimensional modulation, which ensures that the modulation accuracy of the optical field remains unaffected by fabrication errors.
Additionally, except for EU, crosstalk and multiplexing efficiency, we emphasize that the proposed full-modulation dielectric geometric-phase metasurfaces can introduce extra flexibility into the multiplexing principle. Regarding the possible combinations of input/output conditions, the polarization itself only has two orthogonal states in this system, therefore only 2 polarization channels are exactly independent. However, our proposed system can also multiplex linear momentum, i.e., the diffraction angle, of the generated holographic images. In principle, the angular resolution of the system can be high, and the combination of 2 polarization channels and many angular channels can result in numerous possibilities. Furthermore, although the holographic images generated have only two independent polarization channels, the specific polarization angle serves as a crucial factor in encrypting holographic information. In this setup, only the creator of the metasurfaces possesses the knowledge of the precise polarizations (which can vary according to design), thereby encrypting the information. Meanwhile, since the full-modulation metasurface can record the complete nearfield information (spatial amplitude, spatial phase, spatial polarization) of the light, the proposed multiplexing technology is not confined to transverse momentum and polarization dimensions; rather, it can be further extended and implemented to other multiplexing technology such as OAM multiplexing, vector mode multiplexing, more general structured light multiplexing, etc, leading to promising versatile potential to further explore.
-
In this work, we propose and demonstrate a multi-dimensional multiplexing meta-hologram method based on the full-modulation dielectric geometric-phase metasurface. Such a geometric-phase metasurface, consisting of the silicon nitride nanobars as the anisotropic elements, can tailor the spatial amplitude, phase, and polarization of light simultaneously and independently with ideal efficiency. We analyze the corresponding relation of the electric fields between the hologram plane and the image plane. Then, we design the accurate construction of complex imaging multiplexing based on the full-modulation metasurface, which can completely record complex multi-dimensional multiplexing holographic images. We demonstrate different applicable scenarios based on the input-output conditions and achieve on-demand holographic image retrieval. In contrast to conventional multiplexing methods lacking full-modulation capability, a pivotal distinction lies in our introduction of full-modulation dielectric geometric-phase metasurfaces, which offer enhanced robustness to fabrication imperfections and operate across a broader frequency spectrum. Leveraging this full-modulation capability, our proposed meta-holograms feature the capability of more accurate and versatile image construction. This advancement is crucial for future applications in optical information storage, broadcasting, and encryption, promising significant enhancements in communication capacity and confidentiality through multi-dimensional concealment of genuine information.
-
This work was supported by the National Natural Science Foundation of China (NSFC) (62125503, 62261160388, 62375098), the Natural Science Foundation of Hubei Province of China (2023AFA028), the Hubei Optical Fundamental Research Center (HBO2025TQ004), the Major Program (JD) of Hubei Province (2023BAA012), and the High Quality Development Special Project of the Ministry of Industry and Information Technology.
Multidimensional multiplexing geometric phase metaholography
- Light: Advanced Manufacturing , Article number: (2025)
- Received: 20 January 2025
- Revised: 29 July 2025
- Accepted: 13 August 2025 Published online: 30 September 2025
doi: https://doi.org/10.37188/lam.2025.064
Abstract: Meta-holograms, the computer-generated holograms assisted with nano-structured metasurfaces, promise efficient recording of light at the nanoscale. Adopting the multiplexing principle further bestows meta-holography with superb capacity for information storage and imaging applications. However, conventional meta-holograms mostly employ a single physical dimension to multiplex the holograms with incomplete light modulation, which imposes critical limitations on holography fidelity. To address this challenge, here we propose and experimentally demonstrate multi-dimensional multiplexing meta-holograms using full-modulation dielectric geometric-phase metasurfaces. Such metasurfaces enable simultaneous, independent, and arbitrary control of the amplitude, phase, and polarization of spatial light based on the geometric-phase principle, with broadband properties. Thanks to the full-modulation principle, the metasurfaces enable the meta-holograms to multiplex multiple holographic images with engineered patterns, polarizations, and directions, depending on the particular input and output conditions. Compared with the holograms acquired with incomplete light modulation, the designed meta-holograms not only inspire an accurate high-capacity information integration with low crosstalk and ideal energy uniformity, but can also facilitate complex multi-dimensional optical information broadcasting, anti-counterfeit, and encryption in compact optoelectronic devices. This work provides a full-modulation metasurface strategy for robust and scalable multi-dimensional multiplexing meta-holography.
Research Summary
Making multi-dimensional multiplexing meta-holography: a full-modulation dielectric geometric-phase metasurface strategy
Meta-holograms, the computer-generated holograms assisted with nano-structured metasurfaces, promise efficient recording of light at the nanoscale. Adopting the multiplexing principle further bestows meta-holography with superb capacity for information storage and imaging applications. Jian Wang and Jinwei Zeng from Huazhong University of Science and Technology and colleagues now report the development of multi-dimensional multiplexing meta-holograms using full-modulation dielectric geometric-phase metasurfaces. Based on the geometric-phase principle, the metasurfaces enable the simultaneous, independent, and arbitrary control of the amplitude, phase, and polarization of spatial light. This capability supports multi-channel holography with engineered patterns, polarizations, and directions, depending on the specific input and output conditions. The team demonstrates multiplexing multiple holographic images using full Stokes polarization and transverse momentum dimensions, while also incorporating information encryption with low crosstalk.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article′s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article′s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.








 DownLoad:
DownLoad: