Rapid fabrication of reconfigurable helical microswimmers with environmentally adaptive locomotion

Microorganisms can undergo adaptive shape morphing to optimize their locomotion mechanisms in the environment, which enables them to navigate complex barriers and improve survival^1-3. Inspired by this autonomous behavior, artificial reconfigurable microrobots have been proposed to realize similar adaptation capabilities^{4, 5}. Such microrobots primarily rely on active materials (for example, stimuli-responsive hydrogels^{6, 7} and liquid crystal elastomer^{8, 9}) that can respond to external stimuli, including light^{10, 11}, heat¹², and magnetic fields^13-15, and then generate controlled mechanical motion. Among the numerous stimuli-responsive microrobots, helical-like microswimmers are recognized as the most promising tools for in vivo biomedical applications because of their wireless, precise, and biologically harmless actuation under low-strength rotating magnetic fields^{16, 17}. Recently, various alternative schemes have been developed to fabricate shape-morphing helical microswimmers. For instance, self-folding heat-triggered helical microswimmers with reconfigurable shapes and controllable motility have been realized using an origami-inspired ultraviolet (UV) curing process¹⁸. Moreover, helical microswimmers, capable of autonomous swimming by detecting the surrounding temperature changes, have been prepared using a buoyancy-assisted anisotropic gelation method¹⁹. However, although these schemes are usually suitable for producing morphable helical microswimmers of several millimeters, it can be challenging to use them for fabricating microswimmers at the microscale (<100 μm). In fact, many biological structural units are in the microscale range, including cells²⁰, capillaries²¹, and wrinkles on biological surfaces²². Hence, there is an urgent demand for miniaturizing these morphable helical microswimmers to the microscale to deliver and treat single cells, access small and complex environments, and enhance the accuracy of targeted therapy.

Numerous methods, including self-scrolling^{23, 24}, glancing angle deposition (GLAD)²⁵, and template-assisted deposition²⁶, have been developed to generate miniaturized helical microswimmers. However, these techniques are not applicable to active-material curing and morphable microswimmer fabrication. Femtosecond direct laser writing (fs-DLW), which is capable of multiple material printing, excellent 3D geometry design, and nanometer spatial resolution, has evolved into an outstanding method for fabricating reconfigurable helical microswimmers at the microscale^{27, 28}. These microswimmers can respond to multiple stimuli and find applications in drug delivery and release^29-32. However, the following two challenges are worthy of further exploration. First, fs-DLW is a relatively inefficient fabrication strategy because of its point-by-point scanning³³, and it is difficult to produce large amounts of helical microswimmers in a short time using this strategy. For biological clinical trials in which thousands of microrobots are required, a highly efficient production of microrobots is essential. Second, current research on morphable helical microswimmers mainly focuses on their functionalities (for example, biodegradability^{34, 35} and biocompatibility³⁶), and the adaptive locomotion of morphable microswimmers in complicated environments (for example, inside living organisms) requires further study. For instance, within the body, pH values vary among different tissues (for example, normal cells ~7.4, stomach ~1, intestine ~8.4, and tumor cells <7^37-39) and there are numerous microchannels and obstacles. The ability of a microrobot to sense the external environment and perform adaptive locomotion across these networks is vital for in vivo targeted therapy. Consequently, there is high demand for a method to address these two difficulties.

In this study, we developed a rotary holographic processing strategy to fabricate pH-responsive helical hydrogel microswimmers (<100 μm) in a highly efficient manner (<1 s), which enables adaptive locomotion response to the surrounding environment. Based on this strategy, a 3D helical holographic femtosecond laser was generated to print helical microswimmers of different sizes (diameter and height) and morphologies (spirulina-, Escherichia-, sperm-, and Trypanosoma-like) in an easy and rapid one-step process. Compared with the traditional point-by-point scanning strategy, our method involved the use of a 3D-shaped laser to fabricate microswimmers one by one, which is approximately 100 times faster³⁴. By altering the solution pH value, the helical microswimmers underwent tumbling motion in a contracted state and corkscrewing motion in an expanded state under a constant rotating magnetic field. This motion transition was due to the environmentally adaptive shape morphing of the microswimmers, rather than from adjusting the magnetic field. Moreover, the tumbling-to-corkscrewing transition enabled our microswimmers to traverse complex terrains (microwalls and microchannels) and realize targeted drug (DOXs) delivery. The proposed scheme opens an avenue for highly efficient production of shape-morphing helical microswimmers for accurate medical tasks.

To solve the problem of the low-throughput fabrication of fs-DLW, holographic femtosecond laser processing has been reported as a robust way to modulate the laser beam into various 3D light fields, including multifocal spots⁴⁰, Bessel beams⁴¹, and Airy beams⁴². This method is also suitable for rapidly fabricating microrobots. Fig. 1a illustrates the principle of rapid fabrication of a microhelix based on the rotary holographic processing method (Supplementary Movie S1). A rotary computer-generated hologram (RCGH) was developed by superimposing rotary local phase modulation (RLPM) on a computer-generated hologram (CGH), as shown in Fig. 1b. After being reflected from the spatial light modulator (SLM) loaded with the RCGH, a Gaussian femtosecond laser beam could be modulated into a specific 3D light field (Fig. 1c). The phase-type SLM used was a liquid-crystal-based light modulator with the gray scale value of 0–255, corresponding to a phase delay of 0–2π.

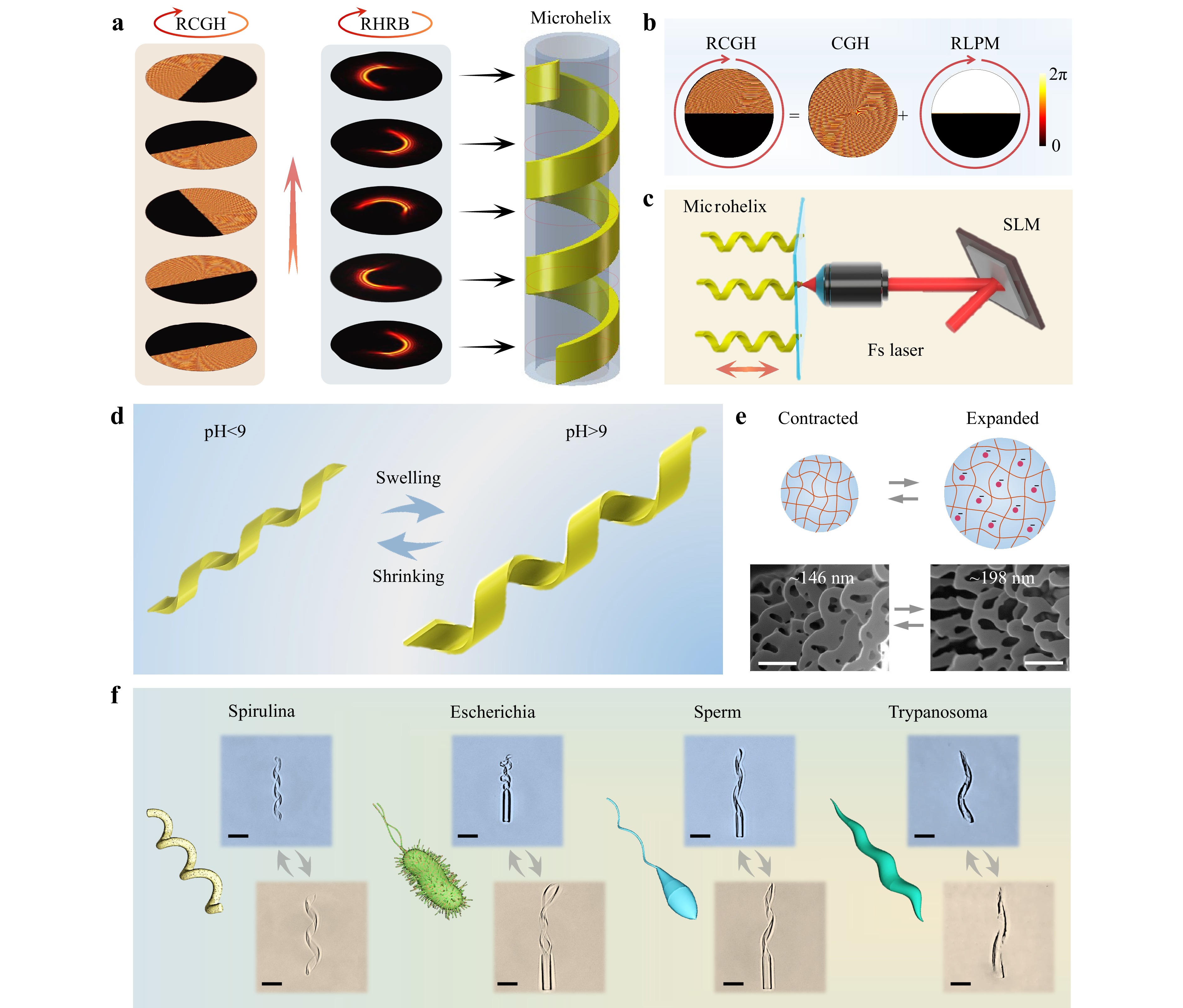
Fig. 1  Schematic illustration of highly efficient fabrication of a stimuli-responsive microhelix based on the rotary holographic processing method. a Rapid fabricating method of the pH-responsive helical structure. The helix is polymerized by the rotary holographic ring beam (RHRB) combined with the sample’s translation. The circular arrows denote the rotation direction of the RCGH and RHRB, and the straight arrow represents the moving direction of the sample. b Generation of the RCGH composed of a CGH and RLPM. c Schematic diagram of the holographic femtosecond laser processing system used to fabricate the microhelix. d Diagrammatic sketch of the expansion and contraction of the pH-triggered hydrogel-based helix. e Shrinking/swelling mechanism of the pH-responsive hydrogel. The upper row shows the schematic mechanism of the expansion and contraction of pH-responsive hydrogels. The bottom row denotes the SEM images of the hydrogel porosities in the contracted (left) and expanded (right) states. Scale bar: 500 nm. f Schematic diagrams of various microorganisms in nature and optical images of the corresponding biomimetic microhelices fabricated using the RHRB in one step. Scale bar: 25 μm.

Initially, a spiral phase plate (SPP), axicon, and blazed grating (BG) were superimposed together to generate the CGH. The SPP and axicon can generate high-order Bessel beams with specific intensity distributions, while the BG is crucial for separating the generated Bessel beams from the zero-order light, which originates from the pixelation effect of the SLM⁴³. Therefore, the final phase distribution of the CGH can be expressed as

where $ {x_0} $ and $ {y_0} $ are the horizontal and vertical coordinates on the SLM plate, $ n $ is the topological charge of the SPP, $ \alpha ={tan}^{-1}({y}_{0}/{x}_{0}) $, $ r=\sqrt{{x}_{0}^{2}+{y}_{0}^{2}} $, $ {r_0} $ denotes the radius of the axicon, and $d$ is the period of the BG. The single laser point was changed into a Bessel ring beam after modulation by the CGH.

To generate RLPM, we superimposed multiple local phase modulations (LPMs) with an increased oblique angle ($ {\theta }_{t} $) in a time sequence using commercial software (GIF Movie Gear) at 20 frames (Supplementary Fig. S1). The LPM was a half-and-half energy-regulated element, where the black area denotes the zero phase with zero energy after regulation, and the white area represents the original phase with unaltered energy^{44, 45}. The Bessel ring beam was changed into a half-ring beam after modulation by this LPM. The time-dependent $ {\theta }_{t} $ can be determined by time ($ t $) and the rotating angle ($ {\theta }_{0} $), which is expressed as

Finally, by adding RLPM to the CGH, the RCGH was synthesized with the following phase distribution:

After modulation by the RCGH, the half-ring beam could become a rotary holographic ring beam (RHRB), as shown in the middle diagram of Fig. 1a.

To fabricate the microhelical structure, a drop of the pH-responsive hydrogel was added to a cover glass that was fixed on a piezoelectric platform (Fig. 1c). Once the RHRB was focused into the hydrogel by an oil immersion lens (60×, NA=1.35), the piezoelectric platform began to simultaneously scan along a straight line in the Z-direction. The rotating ring beam combined with the linear movement of the platform rapidly generated a microhelix, as shown in the right diagram of Fig. 1a. Owing to the fast linear movement of the platform and the rapid rotation of the RCGH, a microhelix could be formed in less than 1 s (Supplementary Movie S1), which is almost 100 times faster than the direct laser writing of microhelices. To demonstrate the high efficiency of our processing strategy, a large array of a thousand hydrogel microhelices was fabricated within 0.5 h, which consisted of the fabrication and mechanical movement times of the sample platform (Supplementary Fig. S2).

The pH-triggered hydrogel was a homemade hydrogel with a pH threshold value of approximately 9 in aqueous solution. Fig. 1d schematically illustrates the response behavior of the hydrogel microhelix, which swelled when the pH exceeded 9 and shrunk when the pH was lower than 9. The 3D morphologies of the microhelices before and after swelling are shown in Supplementary Fig. S3. Our stimuli-responsive hydrogel was a polyacrylic acid (pAAc)-based hydrogel with a mass of terminal carboxyl after polymerization. The swelling and shrinkage mechanisms of the hydrogels are shown in Fig. 1e. When the pH of the solution exceeded 9, the carboxyl lost hydrogen ions and became positively charged. The repulsive forces between the electropositive carboxyls caused the hydrogel to swell. In contrast, when the pH was lower than 9, the electropositive carboxyl combined with a proton and changed into an electroneutral carboxyl⁴⁶. The repulsive force disappeared, and the hydrogel began to collapse. The pH of the solution was adjusted by adding HCl and NaOH solution in turn. To further study the response mechanism of the two-photon polymerized hydrogel, the interior porosities in the contracted and expanded states are shown in Fig. 1e. Obviously, there was an increase in porosity, with the average diameter increasing from 146 (contracted state) to 198 nm (expanded state), which reveals that the expansion of hydrogel is due to water absorption with larger porosity. More details regarding the porosities of the hydrogel are provided in the Experimental section.

The natural world abounds in microorganisms that can serve as templates for developing microhelices with intelligent responses and adaptive locomotion, including spirulina with spiral morphology⁴⁷, Escherichia coli with a head and two helical tails⁴⁸, sperm with a head and one helical tail⁴⁹, and Trypanosoma brucei with a taper-screwed body (Fig. 1f)⁵⁰. These microorganisms can adjust their morphologies and locomotion modes to adapt to the external environment. To prove the universality of our rotary holographic processing method, we fabricated polymorphic biomimetic microhelices in an easy and rapid (<1 s) one-step process. These microhelices can mimic natural microorganisms with shape morphing and adaptive locomotion capabilities. The details of the fabrication process are shown in Supplementary Fig. S4.

To demonstrate the flexibility and designability of our strategy, microhelices with different morphologies involving varying heights (H) and diameters (D) were fabricated. As illustrated in Fig. 2a, the height of the microhelix was controlled by the scanning speed of the piezoelectric platform (V) and rotating angle ($ {\theta }_{0} $) of the RCGH. Meanwhile, the diameter was regulated by the topological charge ($ n $) of the RCGH. When the topological charge was increased from 5 to 40, the diameter of the RHRB increased correspondingly, similar to the diameter of the microhelix. (Supplementary Fig. S5). Fig. 2b reveals the increase in the diameter of the microhelix from 7 to 15 μm as the topological charge increased from 10 to 30. The pitch number of our microhelix throughout was three, which could be set by rotating the RCGH three times during fabrication.

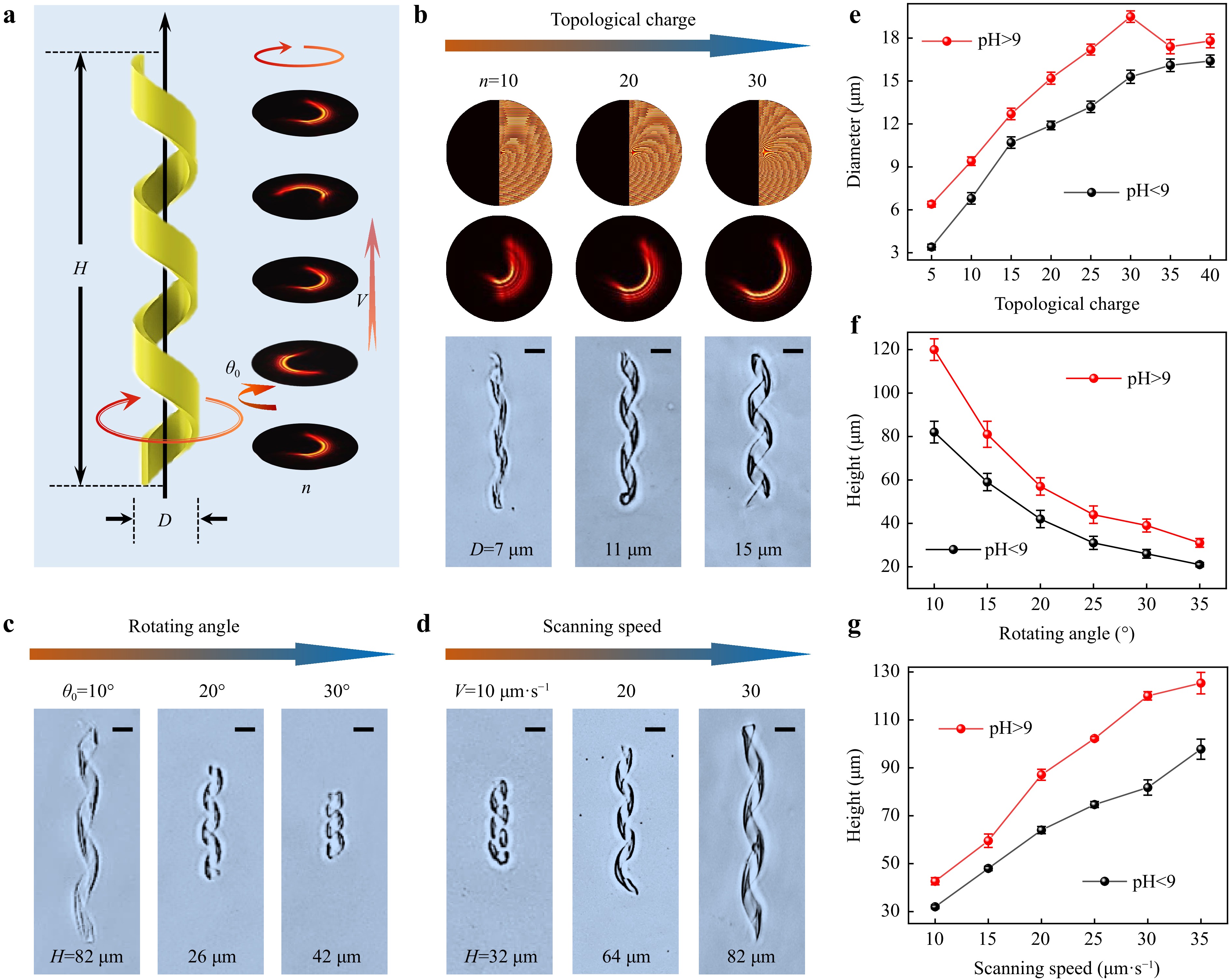
Fig. 2  Microhelices with designed morphologies fabricated using the RHRB. a Diameter D of the microhelix depending on the topological charge n of the RHRB, and the height of the microhelix H controlled by the scanning speed of the sample platform V and rotation angle $ {\theta }_{0} $ of the RHRB. b Diameter of the microhelix increasing with increasing topological charge. c Height of the microhelix decreasing with increasing rotation angle. d Height of the microhelix increasing with increasing scanning speed. e Effect of topological charge on the diameter of the microhelix in the swelling and shrinking states. f,g Effects of rotating angle and scanning speed on the height of the microhelix in the swelling and shrinking states. All scale bars: 10 μm.

Fig. 2c, d show that the height of the microhelix was inversely related to the rotation angle and positively correlated with the scanning speed. The rotation angle ($ {\theta }_{0} $) of the RCGH was the oblique angle difference between the two CGHs of adjacent frames (Supplementary Fig. S1). Obviously, a larger $ {\theta }_{0} $ meant that the RCGH rotated by a circle (360°) with fewer CGHs and shorter fabrication time owing to the fixed frame number (20 frames) and constant pitch number (3). A shorter fabrication time combined with a constant scanning speed of the sample platform decreased the height of the microhelix. As $ {\theta }_{0} $ increased from 10° to 30°, the height of the microhelix decreased from 82 to 26 μm (Fig. 2c). In contrast, a larger scanning speed of the sample platform ($ V $) increased the height of the microhelix, as shown in Fig. 2d, where the height increased from 32 to 82 μm with$ V $ increasing from 10 to 30 μm s⁻¹.

The microhelices illustrated above were all in a contracted state, and there was a slight difference between the contracted and expanded microhelices. Therefore, we further studied the quantitative relationship between the microhelix sizes ($ D $ and $ H $) and the fabrication parameters ($ n $, $ V $, and $ {\theta }_{0} $) in both the contracted and expanded states. As shown in Fig. 2e, in contrast to the positive relationship between the diameter of the contracted microhelix and the topological charge of the RCGH, the diameter of the expanded microhelix decreased when the topological charge ($ n $) exceeded 30. We assumed that this decrease was due to the large diameter of the microhelix in the expanded state. Therefore, the hydrogel microhelix was too soft to maintain its shape. The detailed morphologies of microhelices with different diameters are shown in Supplementary Fig. S6. The dependence of the heights of the microhelices on the rotating angle ($ {\theta }_{0} $) and scanning speed ($ V $) in both the contracted and expanded states is depicted in Figs. 2f, g, where they all demonstrate the same changing trends in the two states. The details of the microhelix morphologies at different heights are shown in Supplementary Figs. S7 with S8.

As a robust microhelix fabrication method, our rotary holographic processing strategy produces microhelices with diverse morphologies. The diameter of the helical microrobot ranged from 7 to 21 μm. The maximum height of the microrobot was determined by the maximum stroke of the piezoelectric platform, which was 200 μm, whereas the minimum height of the helical microrobot (pitch number=3) with clear spiral morphology was 26 μm. In addition to the diameter and height, the pitch number and helical sense of the microhelix could also be easily controlled (Supplementary Fig. S9). Moreover, although the hydrogel-based helical microrobots are prone to deform owing to the small modulus of the hydrogel, our helical microrobot fabricated using the RHRB exhibited excellent morphological and actuation stability.

The polymerized microhelices were immersed in a magnetic Fe₃O₄ nanoparticle (NP, 160 nm) solution (5 mg mL^-1) for 24 h to gain magnetism and become microswimmers (Fig. 3a). The Fe₃O₄ NPs were covered with a nanolayer of SiO₂, which acted as a protective layer to prevent Fe₃O₄ from reacting with the HCl and NaOH solutions (Supplementary Movie S2). Furthermore, hydroxide radicals were modified on the surface of SiO₂ to help the Fe₃O₄ NPs distribute uniformly in deionized (DI) water and attach to the hydrogel microhelix. To characterize the magnetization of the Fe₃O₄ NPs and magnetic microswimmers, a vibrating sample magnetometer (VSM) was used, with the VSM loops illustrated in Fig. 3b, which reveals the soft magnetic behavior of the Fe₃O₄ NPs and magnetic microswimmers.

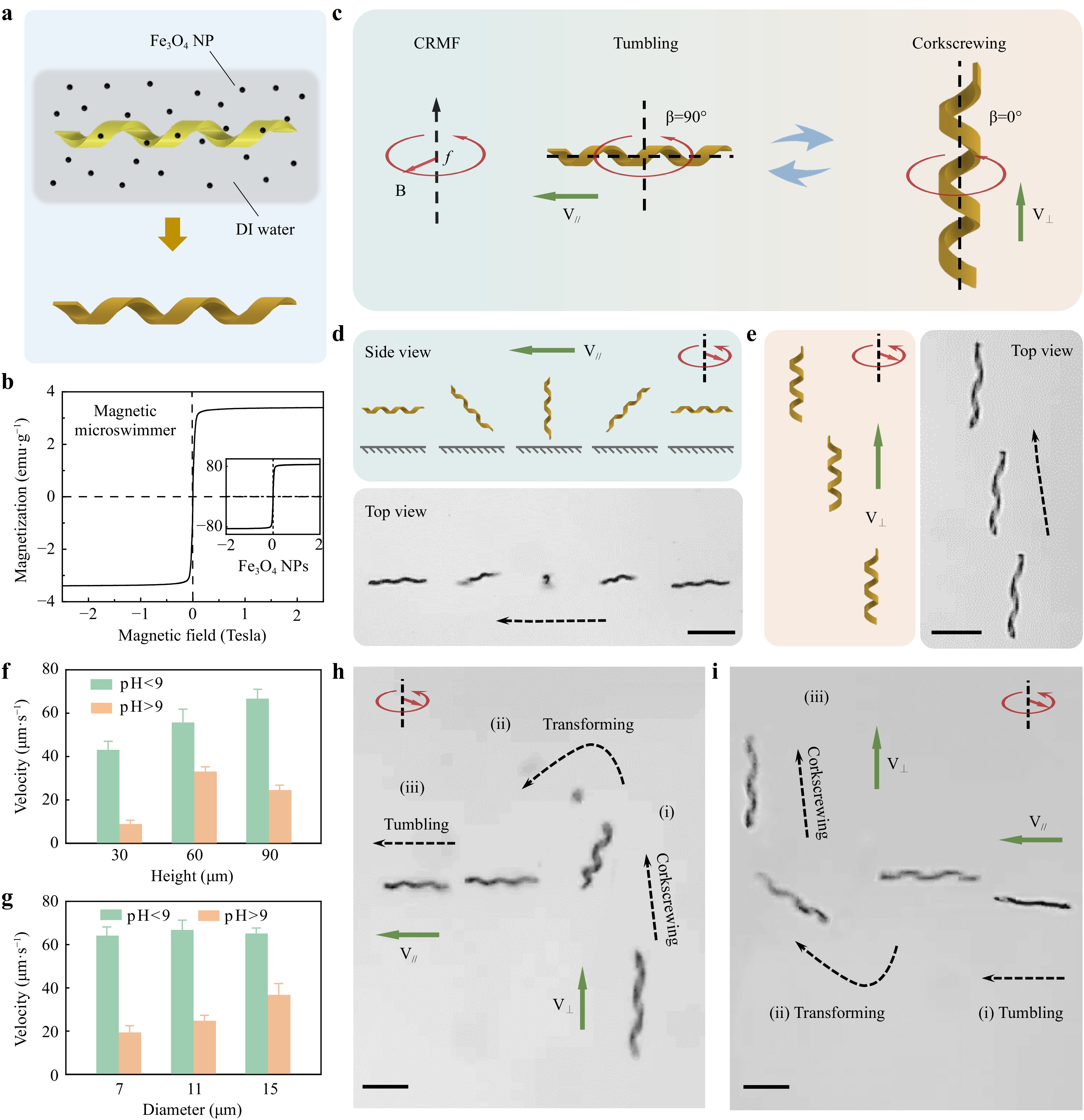
Fig. 3  Adaptive locomotion of shape-morphing helical microswimmers under a constant rotating magnetic field. a Printed hydrogel microswimmer immersed in Fe₃O₄ nanoparticle suspension, gaining magnetism for the actuation test. b Mass magnetization curve of the magnetic microswimmer and Fe₃O₄ nanoparticles measured using a vibrating sample magnetometer (VSM). c Schematics of magnetic actuation for the pH-responsive helical microswimmer in the contracted and expanded states. The contracted microswimmer exhibits tumbling motion with the rotation axis perpendicular to the helical axis, whereas the expanded microswimmer demonstrates corkscrewing motion with the rotation axis along the helical axis. The magnetic field is a constant rotating magnetic field (CRMF) with a strength of 15 mT and a frequency of 5 Hz. d Schematics and time-lapse image of the tumbling motion of the contracted helical microswimmer, where V_∥ indicates that V is parallel to B. e Schematics and time-lapse image of the corkscrewing motion of the expanded helical microswimmer, where V_⊥ indicates that V is perpendicular to B. f, g Velocities of the contracted and expanded microswimmers with different heights and diameters. h Dynamic transition process of the microswimmer from tumbling to corkscrewing. The transition is realized by changing the pH value during the actuation of the microswimmer. i Reverse process compared with h, from corkscrewing to tumbling, owing to the increasing pH value. Scale bar: 50 μm.

The helical microswimmers could be actuated under a rotating magnetic field generated by a homemade triaxial Helmholtz coil system (Supplementary Fig. S10). We first explored the magnetic actuation properties of our shape-morphing helical microswimmer in the contracted and expanded states (Supplementary Note S1 and Fig. S11). Interestingly, a microswimmer demonstrated two different swimming modes in the contracted and expanded states. Specifically, the helical microswimmer performed a tumbling motion in the contracted state and a corkscrewing motion in the expanded state under a constant rotating magnetic field (CRMF), as shown in Fig. 3c and Supplementary Movie S3. The precession angle (β, the angle between the field rotation axis and the helical axis) was 90° for the tumbling motion and 0° for the corkscrewing motion. It is worth noting that the locomotion transition merely relied on the shape morphing of the microswimmer in response to the solution pH value change, rather than on altering the external magnetic field. The helical microswimmer was actuated using a magnetic field with a frequency of 5 Hz and a magnetic strength of 15 mT.

To explain the locomotion transition of the microswimmer, a simplified theoretical model was established, as shown in Supplementary Note S2 and Fig. S12. It has been previously reported that magnetically actuated helical microswimmers exhibit a transition from tumbling to corkscrewing with an increase in the magnetic field frequency^{51, 52}. Tumbling occurs at a low frequency with a precession angle of 90°, while corkscrewing appears at a high frequency with the precession angle gradually diminishing as the field frequency increases. The frequency separating tumbling and corkscrewing is known as the transition frequency ($ {w}_{t} $), which is a function of the external magnetic field and the body geometry and magnetization orientation of the helical microswimmer⁵³. According to this simplified theoretical model, we can derive the transition frequency ($ {w}_{t} $) formulas, where it can be concluded that the diameter ($ D $) is the most important parameter that affects the transition frequency. Clearly, $ {\mathrm{w}}_{\mathrm{t}} $ decreases as the diameter increases. Therefore, a contracted microswimmer with a small diameter exhibits a tumbling motion, whereas an expanded microswimmer with a large diameter exhibits a corkscrewing motion because the actuation frequency is less than $ {w}_{t} $ of the contracted microswimmer but greater than $ {w}_{t} $ of the expanded microswimmer.

Having understood the mechanism of the locomotion transition of the microswimmer, we attempted to separately analyze the swimming characteristics of microswimmers in the contracted and expanded states. To gain deeper insight into the tumbling motion of contracted helical microswimmers, we investigated the detailed locomotion process (Fig. 3d) and mechanism (Supplementary Fig. S13). The schematic diagram and time-lapse image in Fig. 3d show that the microswimmer tumbled forward along its short axis. In addition, a simplified model was established to explain the locomotion mechanism of microswimmer tumbling. The forces exerted on the microswimmer at a certain moment are shown in Supplementary Fig. S13. The tumbling motion can be considered an equilibrium between the magnetic driving torque and drag torque. The drag force originates from the hydrodynamic interaction between the microswimmer and the boundary^{54, 55}. Owing to the distinct boundary conditions, there was a velocity difference between the two ends of the microswimmer, which caused non-coincidence of the mass and rotation centers. Therefore, the contracted microswimmer could move forward. Further details are provided in Supplementary Note S3. By contrast, the expanded helical microswimmer was corkscrewed forward, as shown in Fig. 3e. This corkscrewing motion is consistent with the motion of current helical microswimmers, which can be explained by magnetic helical micromotor propulsion theory⁵⁶. Additionally, experiments to investigate the precise steering of the microswimmers are shown in Supplementary Fig. S14.

There were three major differences between the tumbling and corkscrewing behaviors of our microswimmer: locomotion mode, motion direction, and swimming velocity. First, the locomotion modes tumbled when contracted and corkscrewed when expanded. Second, the contracted microswimmer tumbled forward with a velocity (V_∥) parallel to the magnetic field plane, whereas the expanded microswimmer corresponded to a velocity (V_⊥) vertical to the magnetic field plane. Therefore, the directions of tumbling and corkscrewing were almost perpendicular (Fig. 3c). Third, the swimming velocities of the microswimmers in the contracted and expanded states were quantitatively studied, as illustrated in Fig. 3f, g. We concluded that the tumbling velocities were approximately one–four times larger than the corkscrewing velocities (Supplementary Table S1). More specifically, the tumbling velocity is positively related to the height of the microswimmer and has little relation with the diameter of the microswimmer. The corkscrewing velocity first increases and then decreases with an increase in the microswimmer height and is positively related to the microswimmer diameter. Given the significant velocity difference and steerability of the microswimmer before and after the expansion, we chose the microswimmer with a height of 90 μm and a diameter of 11 μm for the remaining experiments.

After studying and comparing the magnetic actuation properties of microswimmers in the expanded and contracted states, we focused on the dynamic transition process between tumbling and corkscrewing motions, which can be realized by changing the pH value during the motion of the microswimmer. For example, the microswimmer initially expanded and corkscrewed forward (Fig. 3h(i)). The pH of the solution was lower than 9 when HCl solvents were added, followed by shrinkage and transformation of the microswimmer from corkscrewing to tumbling (Fig. 3h(ii)). Finally, the contracted microswimmer tumbled away (Fig. 3h(iii)). In contrast, as illustrated in Fig. 3i, the tumbling-to-corkscrew dynamic transition was realized by altering the solution pH to exceed 9 when actuating the microswimmer. The details of the dynamic transition are shown in Supplementary Movie S4. The dynamic transition of a microswimmer’s locomotion mode relies only on the shape morphing of the microswimmer instead of on the changing of the external magnetic field.

In vivo environments are extremely complex owing to their various biochemistry ingredients and biological obstacles such as folds and cells on the vascular surface, which are primarily within the range of 1–100 μm. Therefore, it is essential to explore smart microrobots that can sense biochemical signal changes and adapt their shapes and locomotion mechanisms to swim across biological obstacles and reach the target position. As a proof-of-concept, we investigated the propulsion and navigation of our helical microswimmer in an in vitro simulation of the biological environment, which could provide admirable technical tools for biomedical applications.

First, we explored the capability of our morphable microswimmer to traverse microscale 3D terrains based on the tumbling-to-corkscrewing transition under a CRMF. A microwall with a width of 10 μm and a height of 60 μm was constructed via fs-DLW (Supplementary Fig. S15a). When the helical microswimmer was in a contracted state and tumbled forward under the rotating magnetic field, it could easily stride over the wall without hindrance (Supplementary Movie S5). However, the expanded helical microswimmer with the corkscrewing motion was blocked by the microwall (Supplementary Fig. S16). Although this expanded microswimmer can swim across the microwall in a corkscrewing motion by precisely adjusting the direction of the external magnetic field, the operational process is complex and time-consuming⁵⁷.

An integrated microchannel with microwalls and a microtunnel was designed to better simulate the complex 3D terrains of an in vivo biological environment (Fig. 4a and Supplementary Fig. S15b). Three walls with a width of 10 μm and a height of 60 μm were fabricated to form two microchannels. As shown in Fig. 4b, the contracted microswimmer was initially in Channel I, followed by rapid tumbling across the middle wall, which could not be realized by the expanded microswimmer. After entering Channel II, the microswimmer began to swell because of the pH change. Fig. 4c shows that the expanded microswimmer could corkscrew through the microtunnel, which could not be accomplished by the contracted microswimmer. Here, the microtunnel was 60 μm in height with a central tunnel width of 25 μm, which was slightly wider than the diameter of the expanded microswimmer. Details of the process of traversing the integrated microchannel are shown in Supplementary Movie S6.

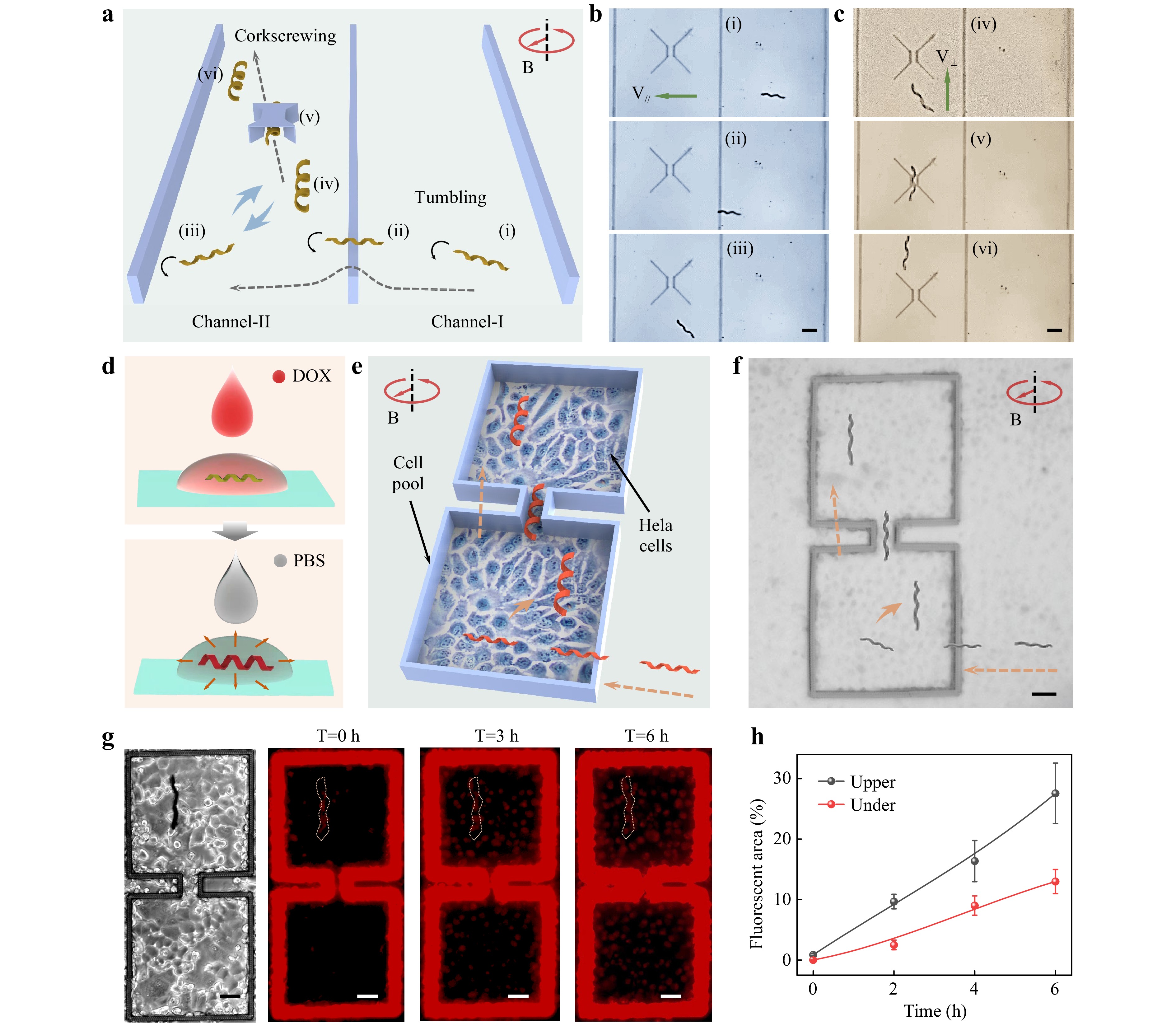
Fig. 4  Demonstrations of traversing complex terrains and targeted drugs delivery based on the tumbling-to-corkscrewing transition of helical microswimmers. a Schematics of the microswimmer traversing complex terrains. The contracted helical microswimmer tumbles across the microwall, and the expanded helical microswimmer corkscrews through the microtunnel. The entire process is actuated by a CRMF. Time-lapse images of the tumbling across the microwall b and corkscrewing through the microtunnel c. d Hydrogel helical microswimmer absorbing a drug in high-concentration DOX solution and spreading drugs in PBS. e Schematics of the microswimmer achieving targeted drug delivery in complex terrains. The contracted helical microswimmer with drugs tumbles into the Hela cell micropool, whereas the expanded helical microswimmer corkscrews through the microchannel and reaches the target position to release the drugs. f Optical image of targeted drug delivery corresponding to e. g Optical image of microswimmer with drugs at the target position, and time-lapse images of the red DOX fluorescence diffusion process. h Quantitative statistics of the DOXs diffusing in the upper micropool (with the microswimmer) and lower micropool (without the microswimmer). Scale bar: 50 μm.

Then, we explored the applications of morphable microswimmers in targeted cargo (microparticles or drugs) delivery where microswimmers traverse complex terrains based on the tumbling-to-corkscrewing transition. The targeted microparticle (MP) delivery is shown in Supplementary Fig. S17, in which an SiO₂ MP with the diameter of 20 μm was directly transported and released. The details of this process are shown in Supplementary Movie S7. Moreover, the hydrogel microswimmer with internal nanopores (Fig. 1f) could carry and release drugs at the targeted position. As shown in Fig. 4d, the hydrogel microswimmer was initially immersed in a DOX solution (1 mg ml⁻¹) for 0.5 h, during which the microswimmer was in contracted state and absorbed DOXs. The microswimmer loaded with DOXs was then transferred to phosphate buffered saline (PBS), where the microswimmer start to swell and releases the drugs. The releasing is realized by the diffusion of DOXs from the nanopores of hydrogel microswimmer. Our earlier study found that this pH-responsive hydrogel can swell in PBS (pH~7.4) without deliberately changing the constituents of hydrogel. We assumed that this is due to the HPQ₄^2- and H₂PQ₄^- in the PBS partially breaking the hydrogen bonds between PAAc and PNIPAAm, and causing the deprotonation of carboxyl groups, which was experimentally validated³⁹. This result makes sure that our hydrogel microswimmers have the potential in biological applications.

On the basis of the tumbling-to-corkscrewing transition and drug diffusion of the hydrogel microswimmer, targeted drug delivery by crossing complex terrains was realized (Fig. 4e). The terrain consisted of a cell micropool fabricated using fs-DLW with HeLa cells cultured inside. The micropool, bound by a microwall with a height of 60 μm and a width of 10 μm, consisted of two square pools connected by a microchannel (Supplementary Fig. S15c). HeLa cells are a type of tumor cell that can maintain good biological viability in solution with a pH value of approximately 7 and have been extensively studied for cell therapy^{58, 59}. Initially, HeLa cells were cultured in a micropool with a pH value of less than 7. Drug-loaded helical microswimmers were transferred to the surroundings of the micropool. Once a magnetic field was applied, the contracted microswimmer tumbled across the wall and entered the lower cell pool. Then, the microswimmer started to swell after adding the PBS solution to adjust the pH value back to ~7.4. The expanded microswimmer corkscrews forward to pass through the microchannel (width ~50 μm), and finally arrives at the upper cell pool (Fig. 4f).

After reaching the target position, DOXs loaded in the expanded microswimmer started to spread and entered the HeLa cells in the vicinity. The optical and fluorescence images demonstrating the diffusion process are shown in Fig. 4g. After six hours of diffusion, HeLa cells in the upper micropool showed larger areas of red fluorescence than those in the lower micropool. Quantitative studies on the comparison of red fluorescence intensity in the upper and lower cell pools were carried out, and the results are shown in Fig. 4h. Statistics indicate that the DOXs were delivered to the targeted position, and there was no visible DOX diffusion along the swimming path. To eliminate the effect of the hydrogel itself on the distribution of red fluorescence, we conducted a control experiment by magnetically actuating the microswimmer without loaded DOXs and found that there was no red fluorescence in the upper and lower cell pools (Supplementary Fig. S18).

Our proposed strategy for fabricating shape-morphing helical microswimmers at the microscale is essential for accurate therapy of cells, tissues, and capillaries. This may confuse researchers because of biomedical applications that exploit the pH value change in the internal environment. Indeed, the critical pH value of our hydrogel was approximately 9 in a strong alkali solution, whereas it decreased to approximately 7.4 in PBS. Therefore, the microswimmer will tumble (contract) in solution at pH<7 and corkscrew (expand) at pH~7.4, which is suitable for biological applications because the pH of normal and tumor environments are 7.4 and <7^{60, 61}, respectively. Moreover, the targeted drug delivery shown above is merely focused on drug diffusion rather than HeLa cell killing, which is a proof-of-concept demonstration and still has greater room for improvement. Further efforts can be made to compound light- or heat-triggered hydrogels that are more biofriendly and degradable. Helical microswimmers with adaptive locomotion based on these hydrogels are expected to promote the progression of microswimmers in future clinical applications.

In summary, a rotary holographic processing method is proposed to fabricate reconfigurable helical microswimmers at the microscale (1–100 μm) with controllable sizes and diverse morphologies easily and efficiently (<1 s), which is approximately 100 times faster than direct laser writing. A helical microswimmer with pH-triggered hydrogel as its base soft matrix and Fe₃O₄ NPs as the actuation material is capable of shape morphing when the pH value of the solution changes. Interestingly, reconfigurable helical microswimmers demonstrate adaptive locomotion under a constant rotating magnetic field, that is, tumbling when shrinking and corkscrewing when swelling. Based on this tumbling-to-corkscrewing transition, an in vitro simulation of the biological environment was conducted by propelling a morphable microswimmer to traverse complex terrains, including microwalls and integrated microchannels. As a proof of concept, we explored the applications of our helical microswimmers in targeted drug (DOXs) delivery to treat HeLa cells after navigating complex terrains, hence validating the application of the reconfigurable microswimmer in accurate treatment and targeted cell therapy.

The system was constructed by integrating spatial light modulation modules into a femtosecond laser direct-writing system. The femtosecond laser was produced using a Ti:sapphire laser oscillator (Chameleon vision-S, Coherent Corp.) with a central wavelength of 780 nm, a repetition rate of 80 MHz, and a pulse duration of 75 fs. After reflection from the liquid-crystal SLM loaded with the CGH (1920 × 1080 pixels, 256 gray levels, a pixel pitch of 8 µm, Pluto NIR II, Holoeye), the Gaussian beam was modulated into a Bessel beam. The Bessel beam was focused into the pH-responsive hydrogel using an oil objective lens (60×, NA=1.35, Olympus). The hydrogel was dropped onto a commercial glass, which was fixed on a 3D nanopositioning stage (E545, Physik Instrumente). By driving the stage along a preprogrammed path while displaying the RHRB, a hydrogel helical microswimmer was printed with high efficiency.

The pH-responsive hydrogel comprised two major components. Component 1 was obtained by adding 0.8 mL AAc (99%), 1.6 g N-isopropylacrylamide (98%), and 0.15 g polyvinylpyrrolidone (Mw~130000) to 1 mL ethyl lactate (98%), followed by ultrasonic mixing for 10 min. Component 2 was obtained by adding 100 μL 4,4′bis(diethylamino) benzophenone into 500 μL N, N-dimethylformamide, followed by ultrasonic mixing for 10 min. The final hydrogel was synthesized by mixing 2.5 mL of Component 1, 600 μL of Component 2, 0.5 mL dipentaerythritol pentaacrylate (98%), and 0.5 mL triethanolamine (99%) together, followed by 12 h of stirring. The hydrogel had to be stored under yellow light to avoid unnecessary light exposure.

The hydrogel microstructures fabricated using femtosecond Bessel beams were immersed in aqueous ammonia (pH > 9) and hydrochloric acid (pH < 9) solutions. After 12 h of freezing in a refrigerator (−80 ℃), the hydrogel microstructures were transferred into a freezer dryer to obtain the freeze-dried contracted and expanded microstructures. The microstructures were then cut using a focused ion beam (FIB) to obtain the internal nanopore morphology, which was photographed using a field-emission scanning electron microscope (SEM).

Hydrophilic DOX was purchased from Sigma-Aldrich. The DOX solution was prepared by adding 1 mg DOXs to 1 mL DI water, followed by ultrasonic mixing for 10 min. After polymerization, the hydrogel microswimmers were developed using isopropyl alcohol for 0.5 h. Next, the microswimmers were treated with UV sterilization for 0.5 h and washed using DI water and PBS solution successively. The microswimmers were then soaked in the DOX solution for 0.5 h to absorb the drugs. Finally, the microswimmers were washed with DI water three times to remove the DOXs from the solution rather than from the microswimmer.

The cell micropool was fabricated via fs-DLW and developed using n-propyl alcohol for 0.5 h. To reduce the fluorescence intensity of the cell micropool, the sample was illuminated with ultraviolet light for 48 h to quench fluorescence. The cell micropool was treated by UV sterilization for 0.5 h and soaked in DI water for 0.5 h and PBS solution for 0.5 h successively. HeLa cells were seeded in the cell micropool and cultured in the cell medium for 48 h, followed by subsequent operations as described above. The HeLa-EGFP cells were obtained from the American Type Culture Collection and cultured in a humidified atmosphere at 37 ℃ with 5% CO₂. The cells were cultured in minimum essential medium supplemented with 1% penicillin/streptomycin and 10% fetal bovine serum (all purchased from Procell Life Science&Technology Co., Ltd.).

Fluorescent images of the cells were imported into the ImageJ software to analyze the fluorescent area. By setting a threshold of 35–255, the red areas in the RED channel of the image could be identified. The rate of the fluorescent area was determined by dividing the total area of the image by the red areas.

This research was supported by the Major Scientific and Technological Projects in Anhui Province (202103a05020005), National Natural Science Foundation of China (Nos. 52075516, 61927814, and 52122511), National Key Research and Development Program of China (No. 2021YFF0502700), Major Scientific and Technological Projects in Anhui Province (201903a05020005), China Postdoctoral Science Foundation (2023M733381 and 2021M703120), USTC Research Funds of the Double First-Class Initiative (YD2340002009), the Joint Fund for New Medicine of USTC (YD2090002016), and the CAS Project for Young Scientists in Basic Research (No. YSBR-049). L.Z. would like to thank the Hong Kong Research Grant Council for support with Project No. JLFS/E-402/18, and the Croucher Foundation Grant with Ref. No. CAS20403. We thank the Experimental Center of Engineering and Material Sciences at USTC for the fabrication and measurement of the samples. This study was partially conducted at the USTC Center for Micro and Nanoscale Research and Fabrication.