Dual-point noncoaxial rotational Doppler effect towards synthetic OAM light fields for real-time rotating axis detection

The rotational Doppler effect (RDE), characterised by a rotating object imparting frequency shifts to scattered beams, has been developed as a promising avenue for achieving robust rotating velocimeters^1–3, universal orbital angular momentum (OAM) complex spectrum analysers⁴, simplified nonlinear RDE metrology systems^5–7, and neotype OAM-based radars^{8, 9}, enabling diverse applications spanning a wide range of industries and fields. In particular, RDE-based rotating-axis detection has attracted significant interest owing to its excellent advantages: ultrafast response, widespread metrological range, and contact-free operation. However, there are several pivotal challenges in real-life applications such as astronomical surveys and various industry scenarios. First, noncoaxial RDE metrology, which is required for most real-world scenarios, is a technical obstacle to be resolved owing to the broadening of the rotational Doppler spectrum; second, probing axis orientations via one-shot metrology, which will saliently increase the processing speed of the detection system, enabling superior detection accuracy and sensitivity; and finally, the low-energy-efficiency light source restricts applications such as long-range celestial body sensing and in vivo detection. Hence, there is a pressing demand to develop a highly efficient detection mechanism for the direct detection of the rotary-axis orientation.

Numerous efforts have been dedicated to the development of multifunctional coaxial RDE (including self-interferometry^{1, 2, 10–15}, heterodyne detection^{16, 17}, a time-varying geometry phase¹⁸, and vectorial Doppler metrology^{19, 20}), and single-point noncoaxial RDE^{21, 22} to acquire the rotating velocity of spinning objects. Despite its superior measurement sensitivity, the former normally requires strict calibration in real settings, which results in complicated and inefficient testing processes. For the latter, the related rotational Doppler spectra suffer from broadening with an increase in the misaligned axis distances, thereby making rotating velocimetry inaccurate²¹. To address this issue, it is important to achieve real-time recognition of the rotating axis orientations for assigned targets. The current detection of rotating-axis orientations is normally realised via multiple measurements (up to four times) by changing the quadrants of a symmetry-broken OAM light field²². However, real-time detection could not to achieved under these circumstances. Moreover, because an asymmetric OAM light source was used, the optical energy efficiency was limited, thereby restricting the detectable range. Consequently, realising real-time, high-energy-efficient, and precise detection of rotary-axis orientation remains a long-term challenge.

Here, we propose a novel concept of the dual-point noncoaxial rotational Doppler effect (DNRDE) and demonstrate a versatile and efficacious detection strategy that enables direct determination of the rotating axis with only a one-shot measurement. To achieve this, we first generated a new type of synthetic OAM light field that maintains orthogonality, perfect rotational symmetry, and high energy efficiency. Based on a well-defined local scatterer model, we further revealed the fundamental mechanism of dual-point noncoaxial rotational Doppler shifts when guiding the tailored OAM beam to interact with a misaligned angular rotator. By quantitatively comparing the two frequency shifts with a prescribed threshold determined by the magnitudes of these two shifts and the quadrant boundary, the orientation of the rotating axis can be determined in real time. In particular, we clarify that our scheme can also achieve accurate probing via four pairs of adjacent dual points that are more sensitive to oppositely oriented rotating axes. Our proposed protocol was verified using a proof-of-concept experiment, which demonstrated an excellent match with theoretical predictions. A general detection system was also demonstrated to map the rotating axis information directly with the aid of optical modal filters. In contrast to existing methods that require multiple measurements, our approach improves the measurement speed fourfold, enabling real-time detection. This work represents a significant advancement in optical RDE techniques, as it not only expands the detection from a single point to a dual point, but also opens possibilities for use in optical metrology and industrial applications.

Fig. 1 shows a schematic of the proposed DNRDE detection scheme for determining the orientation of the rotating axis. We first created a synthetic OAM light field that satisfies the orthogonality and rotational symmetry requirements by exploiting the coherent superposition of specific conjugate-superposed OAM light fields. The synthetic OAM light field was further guided vertically onto the surface of a rotating object with a misaligned rotating shaft O′ relative to optical axis O. Subsequently, the incident tailored light field was scattered from the rough surface of the rotating object. Backscattered light experienced noncoaxial rotational Doppler shifts (RDSs). The orientation of the rotating axis can be unambiguously ascertained in real time by detecting arbitrary dual-point Doppler shifts within two illuminated local scatterers and comparing the magnitudes of these two shifts using a prescribed frequency threshold. Mathematically, synthetic OAM light fields can be produced by the superposition of N (> 1) pairs of conjugate superposed OAM light fields with OAM indices of l_n = 4n or l_n = 2ⁿ⁺¹ (details in the Supplementary Information (SI)), which are formulated in the cylindrical coordinates (r, φ, z) at z = 0 as

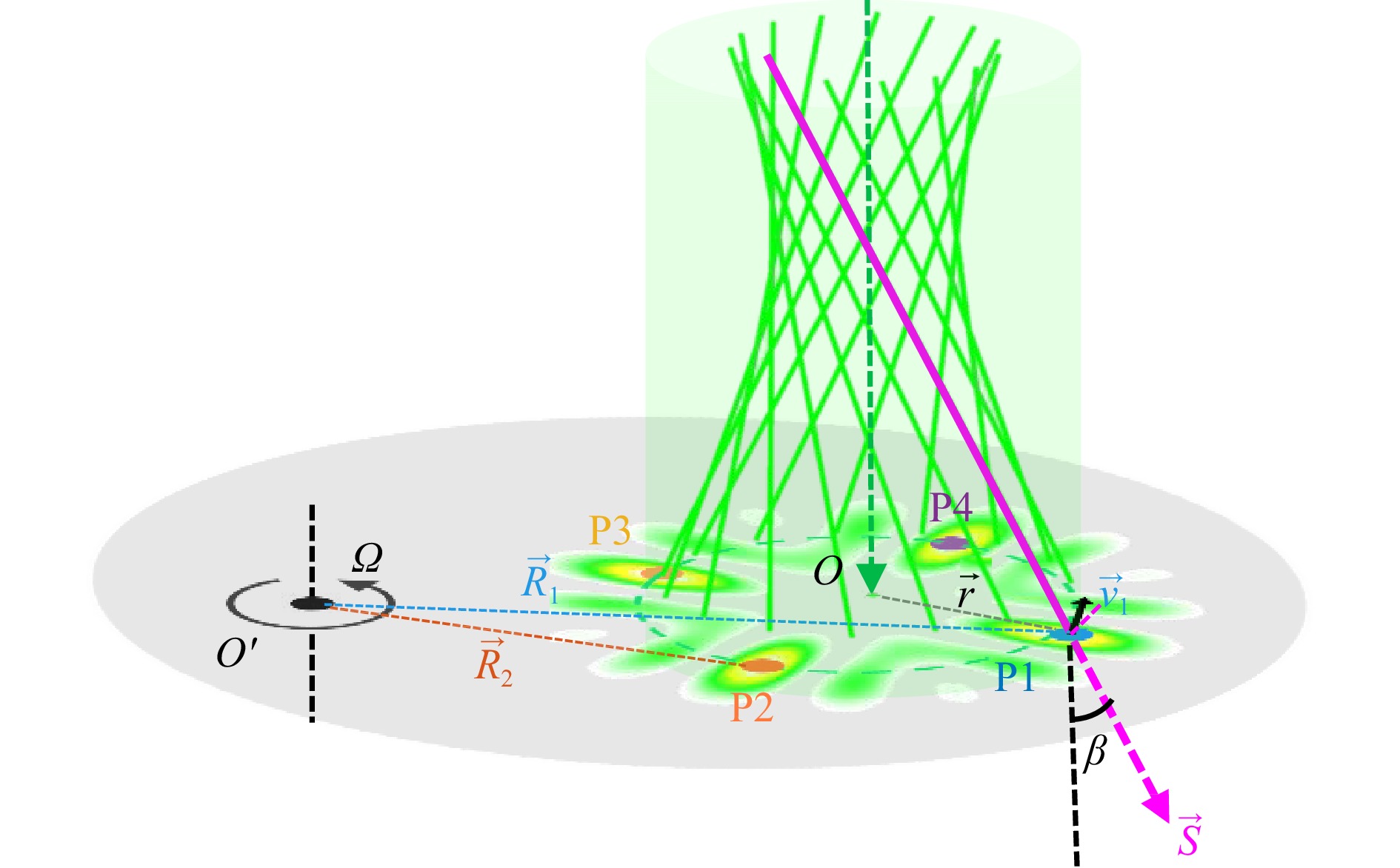
Fig. 1  Diagram of dual-point noncoaxial RDE of customized OAM light fields for rotating-axis detection. The customized OAM light field with four hotspots satisfying the orthogonality and rotational symmetry, is normally directed onto the rough rotating surface with the rotating axis being misaligned with the optical axis optical axis. Two points, P1 and P2, located within the hotspots on the rotating surface were selected. These points experienced distinct RDSs, which are sensitive to the rotating axis orientations. By detecting the two noncoaxial RDSs in the back-scattered light signals, the rotating axis orientations can be unambiguously determined. Here, P1, P2, P3, and P4 are four local scatterers illuminated within four hotspots; Ω represents the rotating velocity; O and O′ are the beam center of the customized OAM light field and the rotating center of the object, respectively; $ \overrightarrow{r} $ and $ \overrightarrow{R} $ are the beam and rotating radii of local scatters; $ \overrightarrow{S} $ is the Poynting vector; and $ {\overrightarrow{v}_{{}_{1}} }$ is the linear velocity at point P1. β is the skew angle of the Poynting vector and optical axis direction.

where E(r) denotes the r-dependent complex amplitude and N denotes the total pair number of coherently superimposed phase-conjugated OAM light fields.

To illustrate our detection scheme, we select E₂ as a representative example, but other synthetic OAM light fields that satisfy Eq. 1 can also be used for this purpose. Fig. 2a–c depict the conjugate superposed OAM light fields E_0,±ln with OAM indices of l₁, l₂ as well as the corresponding synthetic OAM light field distributions with N = 2, respectively. Fig. 2a, b shows that the phase-conjugate superposed OAM light fields exhibit petal-shaped patterns, while in Fig. 2c, four hotspots with orthogonality and rotational symmetry emerge accompanying by tiny sidelobes between the two adjacent hot ones. We also assessed the maximum intensity of the sidelobes relative to the main lobes by scanning the synthetic OAM light field along the x-axis and the line y = 0.8ω₀, as shown in Fig. 2d. The results indicate that the maximum intensity of the sidelobes is < 33%, which would have almost no impact on our detection processes when the echo signals are collected by using the single-mode fibers or optical modal filters.

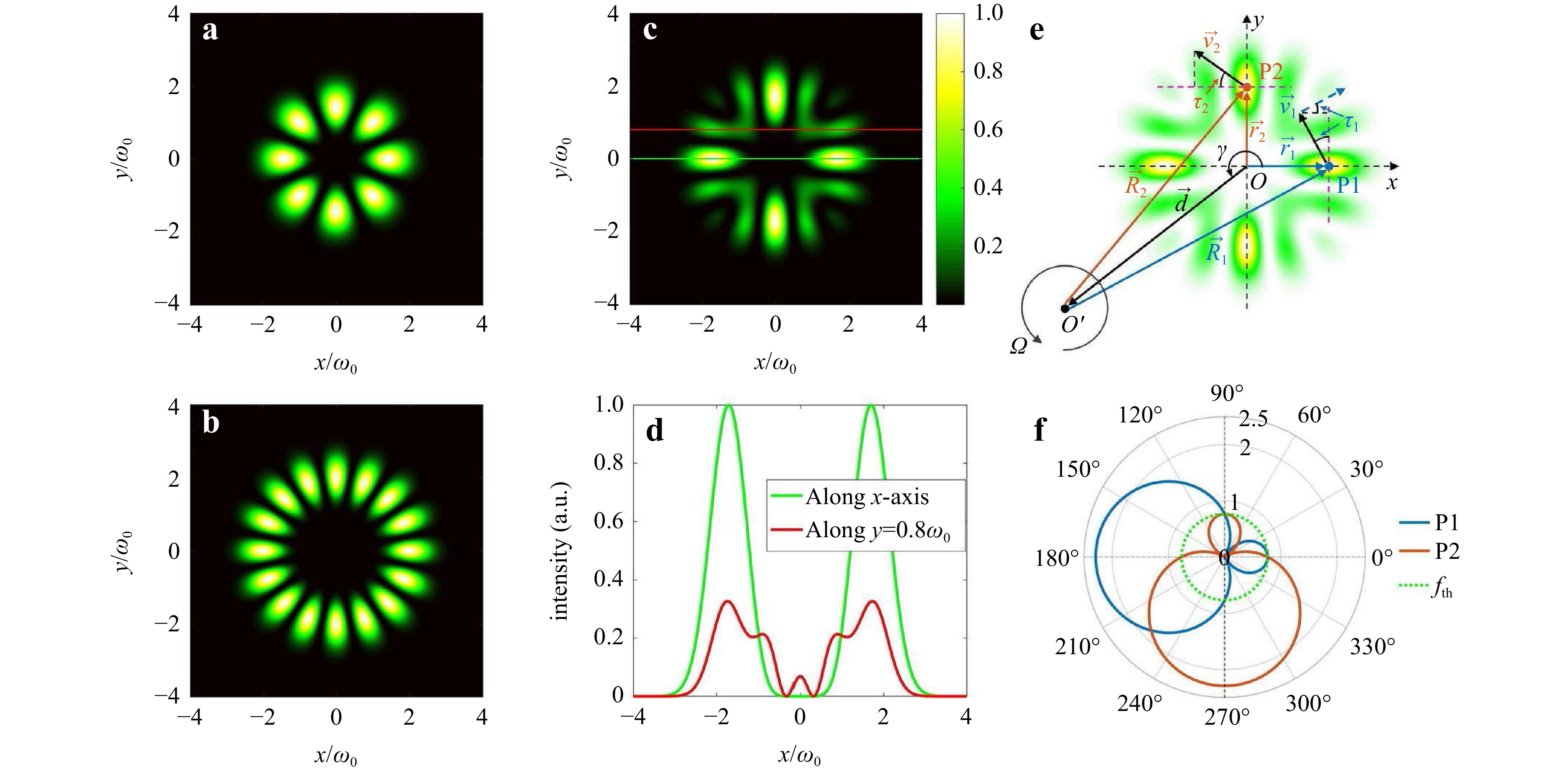
Fig. 2  Concept of the synthetic OAM light field and principle of DNRDE for detecting rotating axis orientations. a and b Light field distributions of two conjugate-superposed OAM light fields with OAM indices l₁ = 4 and l₂ = 8, respectively. c The synthetic OAM light field and d intensity profiles of this customized OAM light field along the x-axis and the line y = 0.8ω₀ for ascertaining the maximum intensity of sidelobes relative to main lobes. e Principle of DNRDE. f Principle for the real-time detection of rotating axis orientations by exploiting the comparison of the relative magnitudes of dual-point noncoaxial RDSs f_RDS-1 at P1 (light blue solid line) and f_RDS-2 at P2 (brown solid line) with a frequency threshold f_th = 763.9 Hz (circular green dotted line) that is determined by the magnitudes of these two OAM-associated shifts together with the quadrant boundaries. Additionally, the polar axis in the polar coordinates denotes the dual-point noncoaxial RDS values, (unit: kHz) and the polar angle represents the rotating axis orientation. All findings were obtained using the following simulated parameters: λ = 532 nm, c = 3 × 10⁸ m/s, ω₀ = 1 mm.

When guiding such a well-established OAM light field onto a rotating rough surface with angular velocity Ω in a noncoaxial manner, the illuminated local scatters on the rotating surface would induce RDSs. We arbitrarily selected two local scatterers on this surface, P1 and P2, that were illuminated by the two hotspots. By simultaneously detecting these two echo light signals, we could determine the DNRDE. By comparing the magnitudes of the dual-point non-coaxial RDSs with a certain frequency threshold determined by these two shifts and quadrant boundaries, the rotating axis can be unambiguously ascertained with only a one-shot measurement. According to the mathematical deviations in Supplementary Note 2, the dual-point noncoaxial RDSs of the customised OAM light field at these two points can be expressed as follows:

Here, $d$ denotes the distance between the rotary and optical axes and $\gamma $ represents the rotating axis orientations. Using Eqs. 2, 3, the orientations of the rotating axes can be determined by measuring the RDSs once the rotating velocity, light beam radius, and axis distance between the optical axis and rotating shaft are known in advance. To demonstrate this, we simulated the dependence of the rotating axis orientations on the DNRDE shown in Fig. 2f, with a preset rotating velocity Ω = 300 rad/s, OAM index l₂ = 8, synthetic OAM light field radius r = 2.5 mm, and axis distance d = 5 mm, which match our upcoming experimental conditions. As shown in Fig. 2f, we first compared a single-point non-coaxial RDS, such as f_RDS-1 at point P1 (light blue solid line), with the frequency threshold. This shift is obviously less than the frequency threshold f_th for the rotating axes in the first and fourth ( I and IV) quadrants, whereas it is greater than f_th for those in the second and third (II and III) quadrants, where f_th = 763.9 Hz (illustrated with circular green dotted lines in Fig. 2f) is the frequency threshold determined by the magnitudes of these two shifts with the quadrant boundaries (Fig. 2f). Obviously, in this case, a single-point noncoaxial RDS fails to distinguish the rotating axis orientations through one-shot measurements because the single-point frequency shift f_RDS-1 in quadrants Ⅰ- and Ⅳ and quadrantsⅡ- and Ⅲ possess the same magnitude rule versus the frequency threshold f_th, respectively. To overcome this limitation, we examined the dual-point frequency shifts (f_RDS-1 and f_RDS-2 at P1 and P2, respectively) and compared them with f_th, as depicted in Fig. 2f. Consequently, we discovered that for the rotating axes in each of the quadrants: in quadrant I, f_RDS-1, f_RDS-2 < f_th; in quadrant II-, f_RDS-1 > f_th, f_RDS-2 < f_th; in quadrant III, f_RDS-1, f_RDS-2 > f_th; and in quadrant IV, f_RDS-1 < f_th, f_RDS-2 > f_th. Therefore, the rotating axis orientations can be discriminated in real time by comparing the magnitudes of the detected dual-point noncoaxial RDSs with the prescribed frequency threshold. Any two local scatterers illuminated within the four hotspots can be selected to detect the noncoaxial RDE and determine the rotating axis orientations.

Furthermore, Fig. 2f shows that the rotating axis in quadrant III elicits significantly larger dual-point non-coaxial RDSs at points P1 and P2, compared to the other quadrants (i.e. the measured points P1 and P2 are lie within positive x- and y-axes, respectively, whereas the simultaneous maxima of f_RDS-1 and f_RDS-2 versus f_th fall into quadrant III). This observation suggests that dual-point noncoaxial RDSs are more sensitive to the presence of oppositely oriented rotating axes. Exploiting these larger shifts can facilitate the highly sensitive and accurate detection of the rotating axes in specific quadrants. Therefore, we further investigate the other dual points in Fig. 4 and find that this phenomenon is consistent across the three pairs of adjacent dual points, namely points 1 and 4, points 2 and 3, and points 3 and 4. By detecting the Doppler shifts at these four particular dual points, full orientations of the rotating axis can be determined with higher sensitivity and thus higher accuracy because the enlarged dual-point noncoaxial RDSs move away from the low-frequency noise domain, leading to a salient signal-to-noise ratio.

In the proof-of-concept experiment, as shown in Fig. S2, we generated a high-quality synthetic OAM light field E₂ using a spatial light modulator with an incorporated 4f system to detect the rotating axis in real time (Methods and Supplementary Notes 3 and 4). To validate the rotating axis orientations, we initially varied the rotating axis orientations to detect the dual-point noncoaxial RDSs in four quadrants (i.e., Ⅰ-, Ⅱ-, Ⅲ-, and Ⅳ) respectively. The axis distance from the optical axis was fixed at 5 mm, while the rotating velocity was set to a pre-determined value of 300 rad/s. The outcomes of the measurements are separately depicted in Fig. 3a–d, where the four individual Doppler signal peaks are detected in the power spectra for each of the measured points. This happened because in addition to the ±4th- and ±8th-order OAM modes, the rotating surface induced RDSs in their interferometric modes (i.e., −4th and +8th or +4th and −8th orders and −4th and −8th or +4th and +8th orders). This experimental finding is in a good agreement that from a previous study². Even after undergoing digital signal post-processing, which introduces strong noise, the signal distribution law is still preserved in the low-frequency domain. Fig. 3a shows that the measured noncoaxial RDSs at points P1 and P2 for ±8th-order OAM modes were all below the frequency threshold f_th. f_th relates to the OAM index that determines the dual-point noncoaxial RDSs, and here it corresponds to the ±8th-order OAM modes. Thus, it is necessary to carefully distinguish the dual-point Doppler signal peaks at matched OAM modes to perform peer-to-peer comparisons. In Fig. 3b, the measured noncoaxial RDSs at points P1 and P2 are 1778.4 Hz (> f_th) and 380.14 Hz (< f_th), respectively. Fig. 3c shows that when the axis orientation is prior-settled in quadrant Ⅲ, i.e., southwest orientation, the measured frequency shifts at points P1 and P2 are both > f_th. In a similar way, in Fig. 3d, the measured noncoaxial RDSs at points P1 and P2 are 471.17 Hz (< f_th) and 1669.66 Hz (> f_th), respectively. The measured outcomes validate our theoretical analyses. For more complicated emitted light fields E_N with N ≥ 3, the Doppler peaks in the measured Doppler spectra multiply. At this point, it becomes difficult to distinguish the Doppler peak corresponding to the prescribed OAM components, thus, leading to an unclear discrimination of the rotating axis orientations. To cope with this issue, we propose a general strategy that uses optical modal filters to sort out specific modal components within scattered light, enabling the detection of only a single Doppler signal peak (the following context). Hence, by comparing the measured dual-point noncoaxial RDSs towards the synthetic OAM light field with the prescribed frequency threshold, the rotating axis orientations can be unambiguously determined.

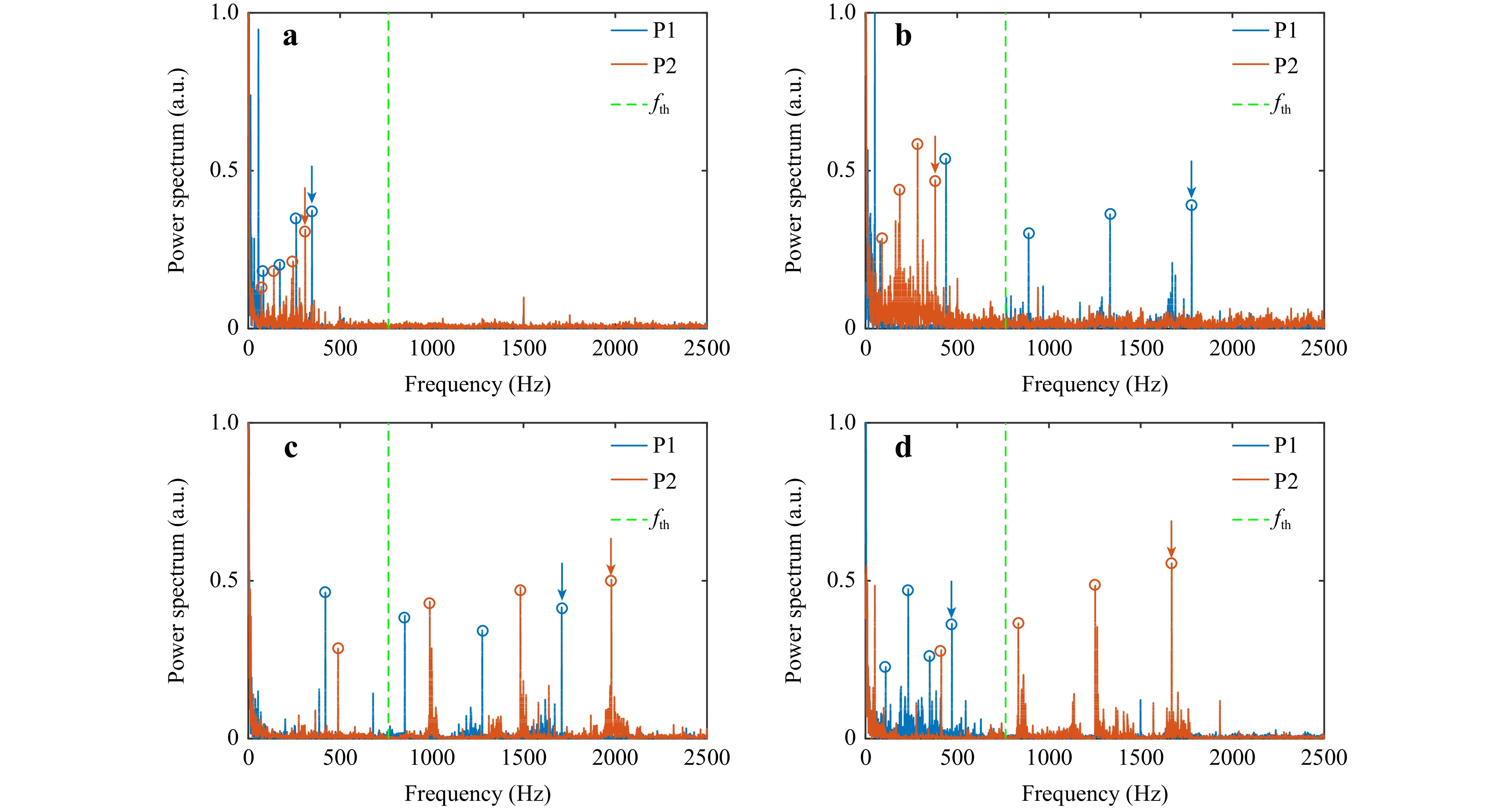
Fig. 3  Measured power spectra as the function of the noncoaxial RDSs at the two points P1 and P2, exploited to determine rotating axis orientations. Dual-point noncoaxial RDSs when the rotating axes are prior-settled in the a I-quadrant; b II-quadrant; c III-quadrant; d IV-quadrant, respectively. The azury and red arrows corresponding to points P1 and P2, respectively, refer to the Doppler signal peaks of ±8-order OAM modes. The frequency threshold f_th = 763.9 Hz (green dotted line).

To further validate our metrological principle for probing rotating axis orientations, we measured distinct dual-point non-coaxial RDSs at points P1 and P3, P1 and P4, P2 and P3, and P3 and P4. As illustrated in Fig. 4, the measured outcomes matched the theoretical predictions well, demonstrating the efficacy of our method in discriminating rotating axis orientations using arbitrarily selected dual points in our engineered light field. Furthermore, Fig. 4a shows that the rotating axes in quadrants II and III are much more sensitive to the Doppler shifts of point 1, whereas point 3 responds more easily to the rotating axes in quadrants I and IV. An identical law is also applicable to the other dual points P2 and P4 (not shown here). In other words, symmetrical dual points (including only P1 and P3, as well as P2 and P4) can be employed to measure axis orientations in real time by comparing their magnitudes with f_th, but in these two cases, the rotating axis fails to be saliently sensible to dual points simultaneously (i.e. ${f_{RDE - 1}}$ and ${f_{RDE - 3}}$ cannot be simultaneously larger than f_th; the same applies to ${f_{RDE - 2}}$ and ${f_{RDE - 4}}$). In contrast, the measured results illustrated in Fig. 4b–d show that the rotating axial orientations are more sensitive to oppositely oriented dual-point noncoaxial RDSs. For example, in Fig. 4b, the detected rotating axis in the northwest orientation triggers more salient Doppler shifts when we measure the dual-point noncoaxial RDSs at P1 and P4 residing on the positive x-axis and negative y-axis (i.e., these two shifts in the northwest orientation (or quadrant II) are larger than the frequency threshold f_th simultaneously). The same principle is validated in Fig. 4c, d. These experimental results are consistent with the theoretical analyses. In practice, this remarkable phenomenon can be further implemented for highly sensitive and accurate detection of the rotating axis after the rotating axis orientation is estimated (through the cherry-picked dual points possessing frequency shifts greater than the frequency threshold simultaneously). This is because larger shifts can move away from the low-frequency noise domain, thereby leading to a significantly higher salient signal-to-noise ratio. Hence, the rotating axis in quadrants I, II, III, and IV could be accurately measured using four pairs of adjacent dual points: P3 and P4, P1 and P4, P1 and P2, and P2 and P3, respectively.

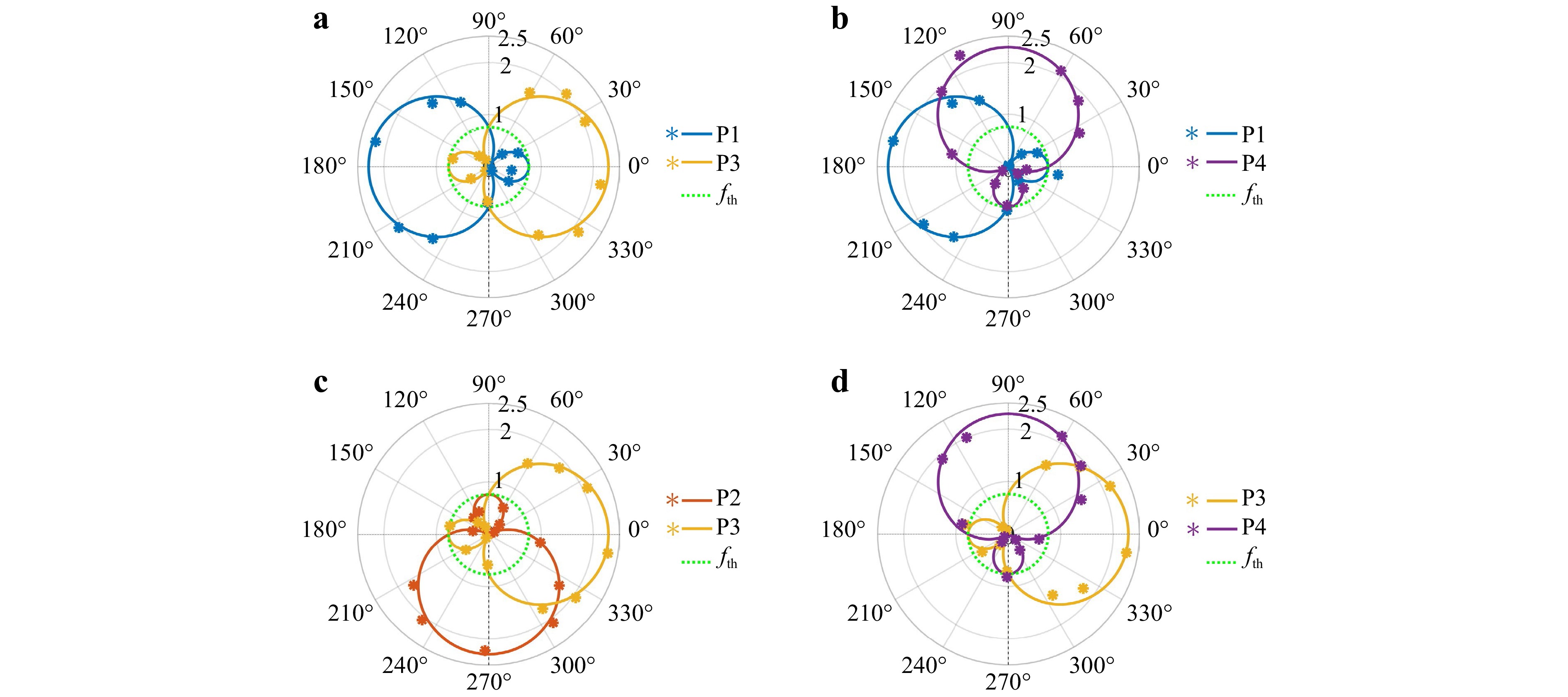
Fig. 4  Detection of the rotating axis orientation via other dual-point noncoaxial RDSs. Measured dual-point noncoaxial RDSs at points a P1 and P3; b P1 and P4; c P2 and P3; as well as d P3 and P4. The asterisks denote the measured values, whereas the solid lines indicate the theoretical predictions. The frequency threshold f_th = 763.9 Hz (circular green-dotted line).

As stated above, with an increase in the linearly coherent superposed light fields (i.e., N > 2 the Doppler peaks in the measured Doppler spectra become more complicated. Doppler peaks are induced by self- and cross-interference between different modal components of the OAM light. At this point, it becomes difficult to distinguish which Doppler peak corresponds to the prescribed OAM components, leading to an unclear discrimination of the rotating axis orientations. To address this issue, we propose the use of modal filters to sort specific modal components within the scattered light, allowing the detection of only a single Doppler signal peak. Consequently, by comparing the dual-point non-coaxial RDSs with the prescribed frequency threshold, the rotating axis can be unambiguously determined for arbitrarily synthesised OAM light fields.

Fig. 5a illustrates an experimental configuration of this general strategy to discriminate rotating axis orientations. The core elements in the proposed detection setup include a pair of optical modal filters, comprising two spatial light modulators (SLM1 and SLM2), two lenses (L5 and L6) as well as two avalanche photodetectors (PD1 and PD2). In practice, the lens can also be replaced by a single-mode optical fiber. The work principle of the optical modal filters is to measure the inner product (sometimes also called the projection measurement) between an incident light field and a loaded basis vector with orthogonality and completeness^23-25. We respectively guide two arbitrary scattered hotspots that are modulated by a noncoaxially rotating surface with velocity Ω into the optical modal filters, and fiter out specific OAM modal components that arise from synthetic OAM light field E_N. Last, we acquire the specific Doppler signals that possess time-varying phase shifts of l_nΩt towards each of OAM eigenmodes by using the photodetectors. The detailed theoretical analyses are given in the Methods section. Here, we only filter out E_0,±ln components and detect solely their Doppler signals, making the Doppler signal peak much simple and more recognizable. After obtaining two noncoaxial RDSs, we can further compare them with a prescribed frequency threshold related to l_n, and thus the rotating axis orientations can be clearly discriminated.

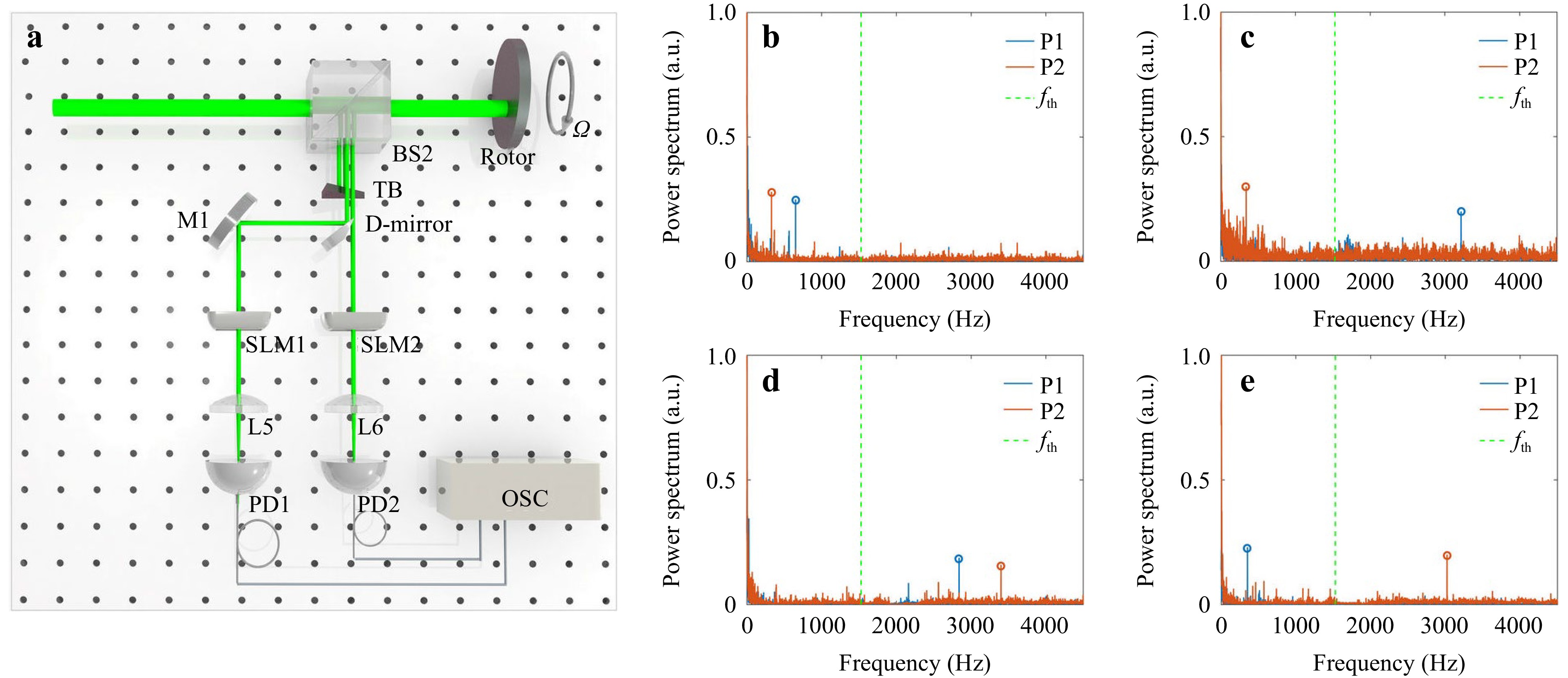
Fig. 5  a Experimental arrangement of a general strategy for detecting rotating axis orientations via arbitrary emitted synthetic OAM light fields E_N. Here, an arbitrarily synthetic OAM light field E_N is launched noncoaxially to the rotating surface. Subsequently, two scattered Gaussian light spots are blocked with a triangular baffle (TB) before two additional Gaussian light spots are reflected by BS2 into a pair of modal filters. Because the two passed light spots are close, we here use a D-mirror to separate these spots into two paths. Subsequently, each path passes through a modal filter (SLM1 and SLM2 as well as L5 and L6) and the filtered signals are detected with an avalanche photodetector (PD), respectively. Finally, the detected analog signals are digitalized by an OSC and displayed on it. b–e Measured Doppler power spectra filtered from modal filters at dual points P1 (bluish solid lines) and P2 (reddish solid lines) by emitting a synthetic OAM light field $ {E}_{4}^{gs} $ with OAM indices of the geometric sequence ln = 2ⁿ⁺¹. Where the rotating axis is preset within b quadrant I; c quadrant II; d quadrant III; and e quadrant. IV The frequency threshold f_th =1528 Hz (green dotted lines) corresponding to ±16th-order OAM components.

As an example, we here select $ {E}_{4}^{gs} $ as the emitted light field (Fig. S1(g)) and $ {\mathrm{\Phi }}_{i}\left(r,\phi \right)={E}_{0,\pm 16} $ as basis vectors to synchronously acquire dual-point noncoaxial RDSs for the effective discrimination of rotating axis orientations. We maintain the axis distance and preset rotating speed constant, and alter the preset axis orientations from quadrants I to IV. Subsequently, we measured the Doppler signal spectra at two points of P1 and P2, respectively, as plotted in Fig. 5b–d. The Doppler signal peaks become single and much easier to be recognized. Therefore, we can discriminate the rotating axis orientations by comparing the corresponding dual-points RDS magnitudes and a frequency threshold. Note that the frequency threshold f_th relates to the filtered OAM orders, which here is f_th =1528 Hz corresponding to ±16th-order OAM components.

Similarly, the rotating axis orientations can also be discriminated by acquiring the noncoaxial RDSs at the other dual points. The simulated and measured results are shown in Fig. 6a–d, respectively. We can see that arbitrarily selected dual points can be used to detect the rotating axis orientations. The measured results are in good agreement with the theoretical simulations. Additionally, it is worth noting that as the filtered OAM orders increase, the matched dual-point noncoaxial RDSs also increase. Such an enlarged frequency shift by increasing N values of the emitted synthetic OAM light fields or the filtered OAM index in Eq. 6, can also be used for accurate discrimination of the rotating axis information. Additionally, the oppositely oriented rotating axes can also be sensitively and accurately discriminated by four pairs of adjacent dual points because of the further enlarged frequency shifts, leading to a salient signal-to-noise ratio, which is consistent with Fig. 4. Based on the discrimination approach proposed above, we accurately measured the rotating axis within full orientation. The meteorological results are shown in Fig. 6e. Each data point was measured 20 times, and the statistical values were used in the final result. We observed that the measured values were in perfect agreement with the prior-settled axis orientations. The maximum absolute measurement errors of the rotating axis orientations, which are principally derived from the limited frequency resolution, were extremely small at approximately 2.23°. This could be further reduced by increasing the sampling time. Overall, we proposed and demonstrated a more general strategy for rapidly and efficiently discriminating rotating-axis orientations.

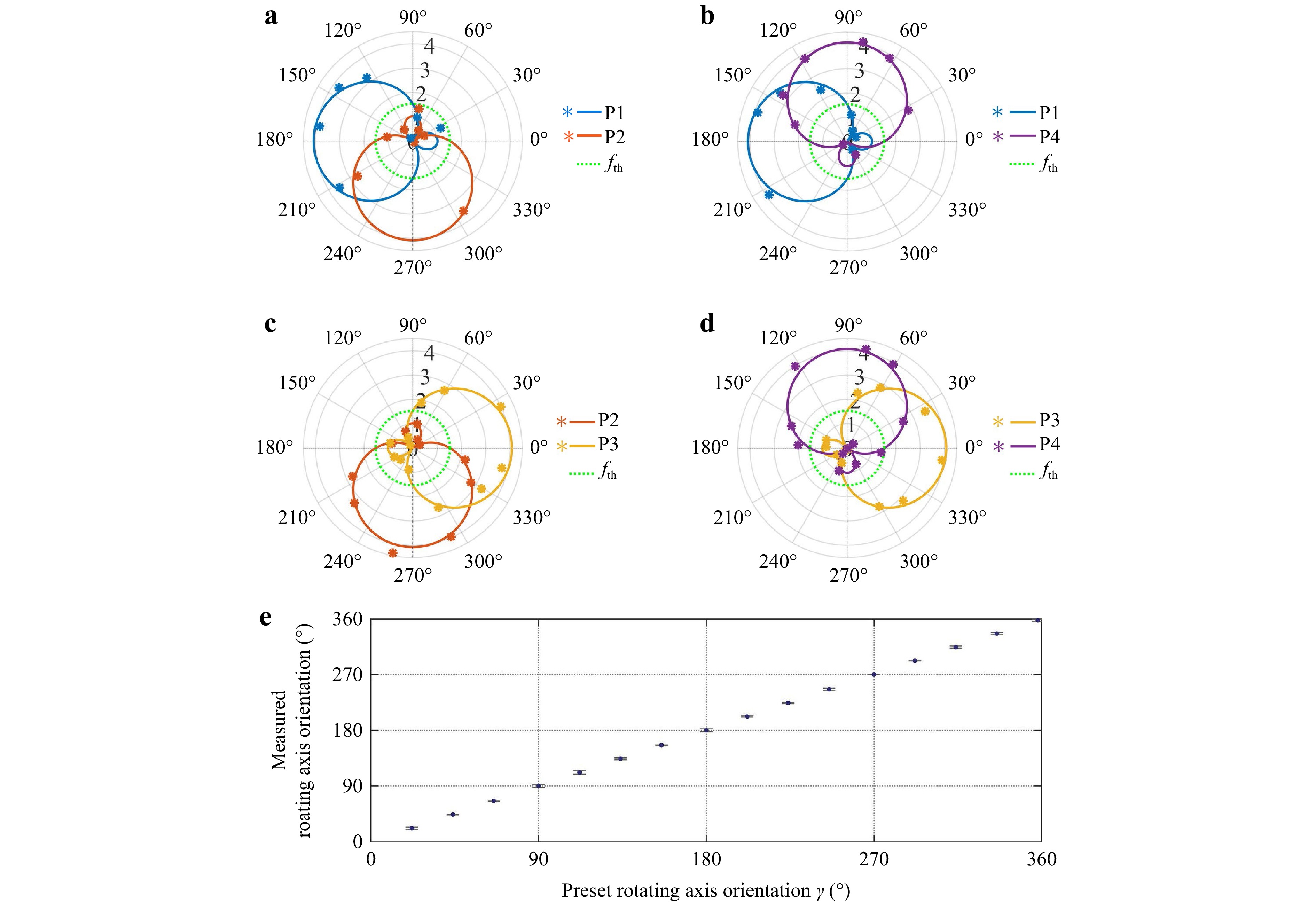
Fig. 6  Noncoaxial RDSs for arbitrary dual points when rotating axis resides in full quadrants. a–d Emitting $ {E}_{4}^{gs} $ field and uploading ±16th-order OAM components onto two modal filters, and then measuring Doppler shifts at dual points a P1 and P2; b P1 and P4; c P2 and P3; d P3 and P4. The asterisks denote the measured values whereas the solid lines indicate the theoretical predications. e Accurate detection of full orientations of the rotating axis via particularly selected four pairs of adjacent dual-points when the rotating axis is prior-settled in distinct orientations. The frequency threshold f_th = 1528 Hz (circular green dotted lines) corresponding to ±16th-order OAM components.

In contrast to state-of-the-art technologies for discriminating rotating-axis orientations²², our metrological approach offers three advantages. First, we adopted a four-hotspot OAM light mode that satisfies orthogonality and high rotational symmetry instead of the symmetry-broken optical vortex as the emitted light in Ref. 22. This significantly enhances the energy efficiency, thus resulting in a more salient detectable range. Second, we compared the dual-point noncoaxial rotational Doppler shifts with a frequency threshold to discriminate the axis orientations, whereas Ref. 22 requires a sequential comparison of the frequency shifts from the emitted segment of the optical vortex within the four distinct quadrants. Consequently, we can determine the axis orientations directly and in real time via a one-shot measurement, whereas the previous method requires four separate measurements for each quadrant. Therefore, the measurement speed is four times higher than that of the previous method. Specifically, the sampled time length is 0.1s under the condition of 10 Hz frequency resolution; thus, real-time performance gives a detection frame rate of 10 fps. Finally, we proposed a dual-probe technique as our detection approach, allowing us to accurately determine the axis orientations via four cherry-picked pairs of dual points, instead of relying on a single-point detection method as in prior works²², thereby improving the accuracy and reliability (that is, the maximal absolute measurement error has been improved from 3.2° in Ref. 22 to 2.23°), under the same experimental conditions. Overall, our metrological approach offers significant improvements over existing methods and provides a more reliable and accurate means of measuring rotating-axis orientations.

Beyond that, compared with a very recently published work²⁶, the differences with our work reside mainly in the following two aspects: on one hand, different light sources were used. The sources designed in Ref. 26 are based on the spliced principle with step functions, which possess distinct OAM orders corresponding to the three quadrants and are essentially symmetry-broken optical vortices. Our synthetic OAM light fields were obtained based on the coherent superposition principle using the superposition of multiple pairs of phase-conjugated OAM light fields that maintain rotational symmetry and orthogonality. On the other hand, there is a salient difference in the detection principles. Ref. 26 used the existing single-point detection method, where the rotating axis orientations could be recognised by comparing three middle Doppler shifts. We exploited a novel dual-point detection paradigm in which the rotating axes can be discriminated by measuring two adjacent Gaussian-type hotspots and further comparing these two shifts with a prescribed frequency threshold determined by the quadrant boundaries.

The prompt detection speed of rotating axis orientations plays a significant role not only in fundamental rotating velocimetry but also in practical application scenarios. Fundamentally, because the signal-to-noise ratio within the detected rotational Doppler spectrum is maximal only if the rotary axis aligns with the light axis of the OAM light field, thereby resulting in high-precision rotating velocimetry, finding the rotating axis in real time is necessary to locate the rotating centring. A typical example is the aviation industry^{27, 28}. During the take-off or landing of a large passenger aircraft, its two wingtips generate large vortices with diameters of several meters. In such scenarios, high-precision and real-time rotating velocimetry of these vortices is crucial to ensure flight safety, which strongly depends on the rapid detection of the rotating axis orientations. In another possible industrial detection scenario, a rotating substance in the workshop can be recognised as a noncooperative body without any specific label, and its rotating centre might change constantly and cannot be directly identified by the human eye. Rapid discrimination of the rotating axis, together with the combination of other automatic pose processing, allows access to precise assembly, processing, and manufacturing^29-31.

In conclusion, we demonstrated a novel conceptual paradigm of DNRDE that provides access to prompt and efficacious detection of rotating axis orientations, which has not been possible before. This depends on the mutual effect between a synthetic four-hotspot no symmetry breaking (OAM) light field and a rotating object with misaligned axes based on the local scatterer model. We show that by making a comparison with a prescribed frequency threshold, arbitrary dual-point non-coaxial RDSs allow the detection of rotating axis orientations in one shot, which is fundamentally impossible in single-point metrologies. In particular, four pairs of adjacent dual-point non-coaxial RDSs afforded unprecedented sensitivity for accurately probing opposite-directional rotating axes. We further show that such a dual-point detection technique is robust to generalised synthetic OAM light fields with the assistance of optical modal filters. The principle demonstrated here not only has profound implications for the further development of multi-point Doppler sensing revealing three-dimensional dynamic characteristics, which were not previously assessable, but also provides more insight into how photonic OAM interacts with cell motions in vivo on the microscale. The ability to offer a new multifunctional (real-time, high-energy efficiency, and superior accuracy) avenue for rotating axis detection for the first time is essential for a plethora of applications such as biological detection, celestial body sensing, and real-world industrial detection scenarios. The possible generalisation to establish an inseparable direction-discriminable Doppler protocol with vectorial vortex light fields remains a fascinating topic that has not yet been examined, and can hopefully inspire more interesting explorations in this field.

In our case, two scattered Gaussian light spots were fed into optical modal filters. A Gaussian light spot $E\left( {r,\varphi } \right)$ can be represented by a set of orthogonal basis vectors ${\Phi _i}\left( {r,\varphi } \right)$:

After passing through optical modal filters, the on-axis intensity was calculated using the inner product of Eq. 4, and its square modulus was determined as follows:

where the asterisk denotes the complex conjugate operation. In addition, the orthogonal basis vector ${\Phi _i}\left( {r,\varphi } \right)$ can be represented by multiple cases, such as OAM states, LG modes, or phase-conjugated superposition states. In our experiment, we preloaded the conjugate of the phase-conjugated superposition states onto the SLMs. This basis vector can be characterised as follows:

with $p\; = \;0$. The projected light field intensity can then be measured using photodetectors, which characterise specific Doppler signals. It is worth noting that the Gaussian light spots arise from the customised light field E_N, which is modulated by a non-coaxially rotating object with velocity $\Omega $, thus leading to a time-varying phase shift of l_nΩt towards each of the OAM eigenmodes. Here, we only filter out the E_0,±ln components and detect their Doppler signals, making the Doppler signal peak much simpler and more recognisable. After obtaining two non-coaxial RDSs, we can further compare them with a prescribed frequency threshold related to l_n, thus, the rotating axis orientations can be clearly discriminated.

To validate the effectiveness of the DNRDE scheme in determining rotating axis orientations in real time with high energy efficiency and high accuracy, a proof-of-principle experiment was conceived and conducted, as illustrated in Fig. S3. A single longitudinal-mode laser emitting a continuous-wave beam at 532 nm was coupled with a microobjective (MO) into a single-mode fibre (SMF) to generate a perfect Gaussian mode. The optical polarisation direction of the Gaussian mode was modulated horizontally using a linear polariser (LP), and a half-wave plate (HWP) is employed to control the output laser energy. The Gaussian mode is then reflected from a mirror (M) and passed through a phase-only spatial light modulator (SLM) loaded with a computer-generated hologram in advance, reshaping the mode into synthetic OAM light modes (Fig. S4(f) in the SI). Using a 4f system composed of two confocal lenses (L1 and L2) and an iris, first-order diffractive light with a high-quality synthetic OAM mode can be well filtered. This well-established mode is then split into two paths using a beam splitter (BS1). One path was utilised to register the generated light field distributions dynamically by exploiting a CCD combined with a focused lens (L3). The other was directed towards a noncoaxially rotating object surface (rotor) with a rotating velocity of Ω. Subsequently, the backscattered light from the object is reflected by another beam splitter (BS2) and focused selectively onto two single-mode optical fibres combined with the corresponding single-point avalanche photodetectors (APD1 and APD2) to gather dual-point echo light signals³². In this experiment, the analogue signals were converted into discrete digital counterparts using an oscilloscope (OSC) linked to the photodetectors via cables. The detected echo signals were displayed in real time on a personal computer (PC) connected to the OSC and used to implement the associated digital signal post-processing. It is worth mentioning that signal processing consisted of two key steps: performing the discrete Fourier transform (DFT) for the time sequences and denoising together with smoothing by combining the spectral subtraction method and a digitally encoded Wiener filter. Details of the postprocessing are provided in Supplementary Note 5 of the SI. Eventually, the dual-point noncoaxial RDSs acquired by post-processing can be employed to accurately ascertain the rotating axis orientations.

This work was supported by the National Natural Science Foundation of China (Grant Nos. 62075049 and 11974258) and the Fundamental Research Funds for the Central Universities (FRFCU5710050722, FRFCU5770500522, FRFCU9803502223, and 2023FRFK06007). This study was supported by the Australian Research Council Centre of Excellence (CE230100006).